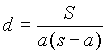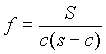Naj bodo točke D, E in F dotikališča stranic in trikotniku včrtane krožnice. Po Cevovem izreku se premice AD, BE in CF sekajo v skupni točki. To točko imenujemo Gergonnovo točko - Ge. Izkaže se, da imajo točke D, E in F naslednje trilinearne koordinate:

D = 0 : e : f; E = d : 0 : f; F = d : e : 0,

kjer je 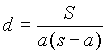, , , 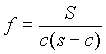S ploščina trikotnika in s polovični obseg.

Naj ima točka X naslednje trilinearne koordinate: X = d : e : f. Z računom (pogoj za kolinearnost treh točk) hitro potrdimo, da leži trojica A, X, D na isti premici (enako tudi trojici B, X, E ter C, X, F). Točka X leži torej na presečišču premic AD, BF in CF, kar pomeni, da se X po definiciji ujema z Gergonnejevo točko. Trilinearne koordinate Gergonnejeve točke so tako: