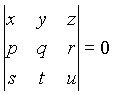Trditev: Naj bodo tri različne točke P, Q in R, ki ležijo v ravnini trikotnika ABC, podane s trilinernimi koordinatami:
P = p1 : p2 : p3
Q = q1 : q2 : q3
R = r1 : r2 : r3
Točke P, Q, R so kolinearne, če je: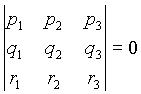
Opomba: Pri delu s trilinearnimi koordinatami se večkrat srečamo s trovrstno determinanto, zato jo zapišimo še v razviti obliki:
Zapis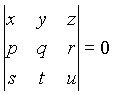 
je
enakovreden enačbi x(qu - rt) + y(rs - pu) + z(pt - qs) = 0
Zaradi principa dualnosti velja analogna trditev o konkurenčnosti premic:
Trditev: Tri premice:
l1x + m1y + n1z = 0
l2x + m2y + n2z = 0
l3x + m3y + n3z = 0
potekajo skozi skupno točko natanko takrat, ko je: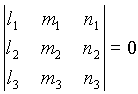
V tem primeru je presečišče premic točka T = m2n3 - n2m3 : n2l3 - l2n3 : l2m3 - m2l3.