TRAPEZI

Trapez je štirikotnik, ki ima eno dvojico vzporednih stranic

                OSNOVNI POJMI                        

Načrtan je trapez ABCD. Stranici AB in CD sta vzporedni. Imenujemo ju osnovnici trapeza. Nevzporedni stranici AD in BC sta kraka trapeza.

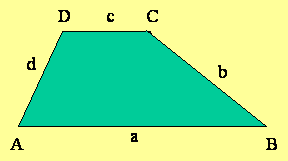
AB = a, CD = c...osnovnici trapeza   AB      DC

AD = b,  BC = d.....kraka trapeza

Pravokotna razdalja obeh osnovnic je višina trapeza.

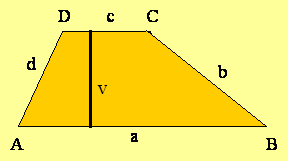
v -  višina trapeza

 Daljica s, ki povezuje razpolovišči M in N obeh krakov, je srednjica trapeza

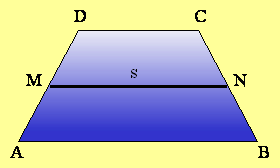
 M in N....razpolovišči krakov

MN = s ....srednjica trapeza

 Kota, ki ležita ob istem kraku sta  suplementarna.

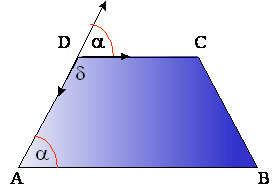
α+ δ = 180⁰

β + γ  = 180⁰

 Oglejmo si še važno lastnost srednjice trapeza!

 V trapezu ABCD načrtaj srednjico MN, skozi krajišče M pa vzporednico EF kraku AD. Trikotnika EBN in NFC sta skladna.

Zaradi skladnosti omenjenih trikotnikov je tudi EB = CF =x

Iz slike vidiš, da lahko zapišeš:

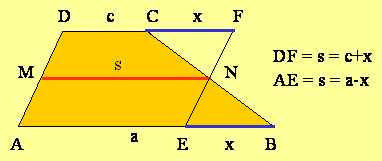
s = a - x

s = c + x

Seštej oba izraza za s:

s = a - x

s = c + x

^{------------------------}

2s = a + c

s =

Srednjica trapeza je vzporedna osnovnicama in je enaka njuni polovični vsoti.

Polovično vsoto dveh števil imenujemo tudi aritmetično sredino teh dveh števil. Srednjica je torej aritmetična sredina obeh osnovnic trapeza.

ENAKOKRAKI TRAPEZ

 Načrtaj trapez ABCD tako, da bosta kraka AD in BC enaka.

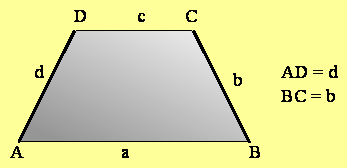
Iz slike lahko razbereš še naslednje lastnosti: 

V enakokrakem trapezu sta kraka enaka

V enakokrakem rapezu sta kota ob osnovnici enaka

V enakokrakem trapezu sta diagonali enako dolgi.

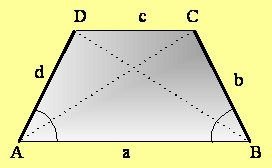
                                                            AC= e, BD = f

                                                           AC = BD