LASTNOSTI
V paralelogramu sta po dva nasprotna kota enaka, po dva sosedna pa suplementarna.
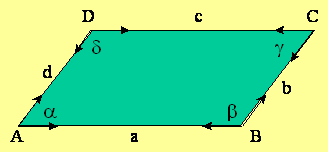
- nasprotna kota sta a in g,
- nasprotna kota sta b in d,
- sosednja kota sta a in b,
- sosednja kota sta a in d.
Kota a in g imata krake vzporedne v nasprotno smer - sta enaka.
Kota b in d imata krake vzporedne v nasprotno smer - sta enaka.
Kota a in b (in še drugi pari) sta kota z vzporednimi kraki
(en par je vzporeden v isto smer, drugi par je vzporeden v nasprotno smer- suplementarna kota)
Zapiši še druge pare sosednjih kotov:
1) a + b = 1800, 2) .................... 3) ................... 4) ...................
V paralelogramu sta po dve nasprotni stranici enako dolgi.

Enaka kota sta a in g, enaki stranici sta a in c.
Enaka kota sta b in d, enaki stranici sta b in d.
Da se o tem prepričaš načrtaj v paralelogramu ABCD diagonalo AC, ki razdeli kot....... v kota ......in......., kot ...... pa v kota......in......Trikotnika ABC in ACD sta skladna (.....=......,
......=......., skupna stranica AC) Ker sta skladna, se ujemata tudi v vseh ostalih enakoležnih sestavinah. Zato je AB=CD in BC=AD
( Stranici AB in CD sta enakoležni,ker ležita nasproti enakima kotoma ..... in....... Prav tako pa sta enakoležni stranici .......in.......,,ker ležita nasproti enakima kotoma....... in......
V paralelogramu se diagonali razpolavljata.
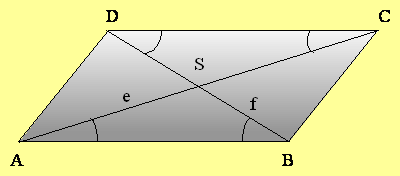
AS =![]() , SC =
, SC =![]() , BS =
, BS =![]() , SD =
, SD =![]() ...... S = razpolovišče diagonal
...... S = razpolovišče diagonal
Načrtaj obe diagonali. Nastala sta skladna trikotnika ABS in CDS.
( Ujemata se v eni stranici AB = CD in v dveh kotih )
Ker sta skladna, sta enaki tudi enakoležni stranici AS in SC ter BS in SD. To pa pomeni, da točka S razpolavlja obe diagonali, ali, kakor pravimo, diagonali razpolavljata druga drugo.
POSLEDICE LASTNOSTI:
Če meri en kot v paralelogramu 900, merijo tudi ostali trije koti po 900; pravimo, da je paralelogram PRAVOKOTEN.
Če sta v paralelogramu dve sosednji stranici enaki, so vse stranice med seboj enake; pravimo ,da je paralelogram ENAKOSTRANIČEN.
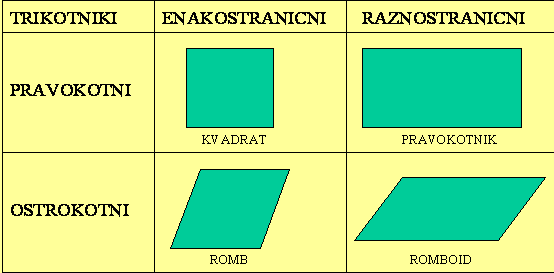
Paralelograme delimo glede na stranice v ENAKOSTRANIČNE in RAZNOSTRANIČNE,glede na kote pa v PRAVOKOTNE in POŠEVNOKOTNE paralelograme.
Enakostranični pravokotni paralelogram imenujemo KVADRAT.
Raznostranični pravokotni paralelogram imenujemo PRAVOKOTNIK.
Enakostranični poševnokotni paralelogram imenujemo ROMB.
Raznostranični poševnokotni paralelogram imenujemo ROMBOID.
Važni sta še lastnosti, ki veljata le za enakostranični in za pravokotni paralelogram, in sicer:
V enakostraničnem paralelogramu se diagonali sekata pravokotno ter razpolavljata kota ob ogliščih.
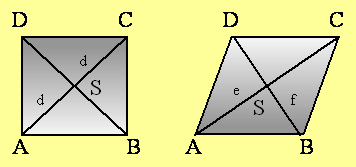
Načrtaj romb ABCD!
Diagonala f = BD razdeli romb v dva enakokraka trikotnika BDA in DBC. Diagonala AC = e je simetrala saj poteka skozi razpolovišče skupne osnovnice BD in povezuje vrha obeh enakokrakih trikotnikov A in C: stoji pravokotno na osnovnici BD.
Pravimo, da se diagonali sekata pravokotno, se razpolavljata in razpolavljata notranje kote.
Ker so diagonale simetrale kotov kot razpolavljajo, ( Vsaka točka na simetrali kota je enako oddaljena od obeh krakov.) je točka S (presečišče diagonal) enako oddaljena od krakov vseh kotov, to je od vseh štirih stranic.
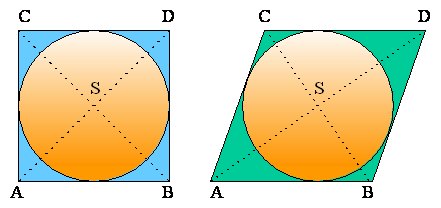
Iz tega sledi, da je možno enakostraničnemu paralelogramu včrtati krog.
Kvadrat Romb
V pravokotnem paralelogramu sta diagonali enako dolgi.
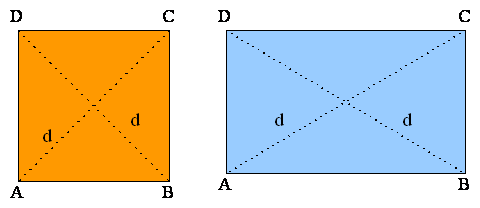
Trikotnika ABC in ABD sta skladna. Ujemata se v dveh stranicah (stranica AB je skupna, BC=AD) ter v pravem kotu, ki ga oklepata. Zato se ujemata tudi v tretji stranici ali AC=BD. Ker se diagonali razpolavljata in sta enako dolgi, so enake tudi polovice SA, SB, SC in SD.
Iz točke S je možno pravokotnemu pararalelogramu očrtati krog.
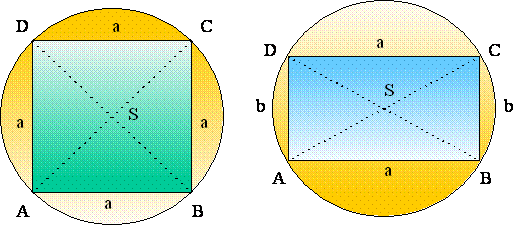
V paralelogramu se razdalja dveh nasprotnih stranic imenuje višina.
Paralelogram ima dve višini, ker ima dve dvojici nasprotnih stranic.
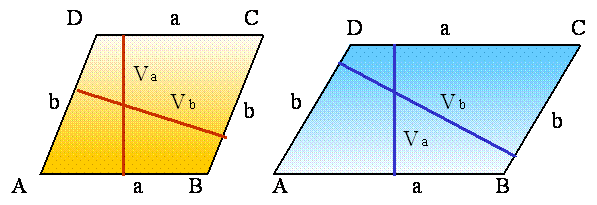
Načrtana sta paralelograma ABCD in višini va in vb , pri čemer je stranica a osnovnica in va ustrezna višina; prav tako je stranica b osnovnica, vb pa ustrezna višina.