a) Potenciranje s celimi eksponenti
Potenca a n je produkt n enakih faktorjev a.
Pogoj: nÎZ, a ¹ 0;
a . a . a . … = a n n faktorjev
Število a, ki ga vzamemo n-krat kot faktor, imenujemo osnovo ali bazo potence, število n, ki izraža število enakih faktorjev a, pa eksponent potence.
Osnova a je lahko poljubno pozitivno ali negativno število, različno od 0.
Iz definicije sledi:
1n =1.1.1… 1= 1
0 n = 0 . 0 . 0 … 0 = 0
Vsaka potenca števila 1 je 1, vsaka potenca števila 0 je 0.
Potence s pozitivno osnovo so pozitivne.
( + a) n = + a n
Potence z negativno osnovo so pozitivne, če je eksponent sodo število, in negativno število, če je eksponent liho število.
(- a) 2n = + a 2n (- a) 2n + 1 = - a2n + 1
b)Računske operacije s potencami
a) Seštevanje in odštevanje
ax n + bx n = (a + b)x n
ax n – bx n = (a - b)x n
Seštevati in odštevati moremo le istoimenske potence, to je take, ki imajo enake osnove in enake eksponente, in sicer po pravilu za seštevanje (odštevanje) enočlenikov.
b) Množenje in deljenje potenc
1b) Množenje potenc z enakima osnovama
a m . a n = a . a . a…a x a . a . a…a = a . a . a…a = a m + n
m-faktorjev n-faktorjev m + n-faktorjev
a m . a n = a m + n
Potenci z enakima osnovama množimo tako, da osnovo potenciramo z vsoto eksponentov.
a m + n = a m . a n
Število potenciramo z vsoto dveh števil tako, da ga potenciramo z vsakim sumandom posebej in dobljeni potenci pomnožimo.
2b) Deljenje potenc z enakima osnovama
m-faktorjev
a m : a n =
![]() = a m - n
= a m - n
n-faktorjev
Potenci z enakima osnovama delimo tako, da skupno osnovo potenciramo z razliko med eksponentom deljenca in eksponentom delitelja.
a m : a n = a m - n
Število potenciramo z razliko dveh števil tako, da ga potenciramo najprej z minuendom, potem pa s subtrahendom ter prvo potenco delimo z drugo.
a m - n = a m : a n
3b) Množenje potenc z enakima eksponentoma
a n . b n = a . a . a …a . b . b . b…b = (a . b). (a .b). (a . b)… (a . b) =
(a . b) n n-faktorjev a n-faktorjev b n-faktorjev ab
a n . b n = (a . b) n
n- ta potenca produkta dveh števil je produkt n-tih potenc posameznih faktorjev.
(a . b) n = a n . b n
Produkt potenciramo tako, da vsak faktor potenciramo posebej.
4b) Deljenje potenc z enakima eksponentoma
n-faktorjev
a n : b n =
![]()
n-faktorjev n-faktorjev
a n : b n
=
![]()
Potenci z enakima eksponentoma delimo tako, da količnik osnov potenciramo z enakim potenčnim eksponentom.
n - ta potenca ulomka je ulomek, ki ima za števec n - to potenco števca, za imenovalec pa n - to potenco imenovalca.
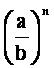 =
=
![]()
c) Potenciranje potence
Potenco potenciramo tako, da osnovo potenciramo s produktom eksponentov.
n - seštevancev
(a m) n = a m. a m. a m… a m = a m + m + m +…+ m = a m . n
n - faktorjev
(a m) n = a m . n
Število potenciramo s produktom dveh faktorjev tako, da ga potenciramo najprej z enim faktorjem, dobljeno potenco pa še z drugim faktorjem.
a m . n = (a m) n
Zaradi komutativnosti produkta velja:
(a m) n = (a n) m
d) Potence a 1, a 0 in a - n
Vsako število potencirano z eksponentom 1, je število samo.
a m . a = a m + 1
a 1= a
Potenca z eksponentom 0 ima pri poljubni od 0 različni osnovi vrednost 1.
a ¹ 0
a m : a n = a m - n , če je m = n je:
a m : a m =a m - m = a o
ao = 1
Potenca z negativnim eksponentom je enaka obratni vrednosti potence z enako osnovo in nasprotnim eksponentom.
n > m ali n = m + x
a m : a n = a m : a m + x = am – (m + x) = am – m – x = a -x
a m : a n = a m
: a m + x = ![]() =
= ![]()
a - n = ![]()
Število potenciramo z negativnim številom tako. da njegovo obratno vrednost potenciramo z nasprotnim potenčnim eksponentom.

Še nekaj pravil:
a m
. a 0 = a m . 1 = a m
a 0 : a – n = 1 :
![]() = a n
= a n
a m . a 0 = a m + 0 = a m a 0 : a – n = a 0 – ( -n) = a n
a m
. a – n = a m .![]() =
= ![]() = a m – n (a n )
0 = 1
= a m – n (a n )
0 = 1
a m . a – n = a m . a m + (- n ) = a m –n a 0 . b 0 = ( a . b)0 =1
a 0 . b 0
= 1 .1 = 1 (a – m )
n = ![]()
(a n
) 0 = a n.0 = a 0 =
1 a – n . b – n = ( a .
b ) –n = ![]()
a – n
. b – n = ![]() .
. ![]() =
= ![]() (a – m ) n = a – m
. n =
(a – m ) n = a – m
. n = ![]() itd.
itd.
PRIMERI:
1. Množenje potenc z isto osnovo
Pravilo: am . an = am + n
1) 2) 3)
a) x3. x7 = a) a4. a3. a -5 = a) 3a3. 5ab2 . 6ab3 =
b) a7 . a -3 = b) 7x7 . 3x4 = b) 4r2v . 3r . 2v3 =
c) a-5 . a2 = c) 3b -3 . (- 4b) = c) 4a2b -3 . 5a -1b5 =
d) a-1 . a -1 = d) (- 5d -1) . (- 4c4.d-3) = d) (3x3y -4) . (-6x -2y5) =
e) x-3 . x -2 = e) (9x4y - 3) . ( - xy4) = e) (- 2abc -1) . (- 3a2b -2c2) =
2. Deljenje potenc z isto osnovo
Pravilo: am : an = am – n
1) 2)
a) a9 : a7 = a) ( - 28a5b2c4) : ( - 2a3b5c4) =
b) 15a7 : 3a4 = b) x3 : x5 =
c) (24x4) : (- 6x3) = c) m3 : m-5 =
d) (16a3b2) : (6ab2) = d) 27x7 : 9x-3 =
e) (9a4) : (3a6) = e) 42m-5 : 7m =
3. Potenciranje potenc
Pravilo: ( am)n = am . n
1) 2)
a) (a3)6 = a) (- x)3 . ((- x)2)3 =
b) (b- 3)3 = b) (a- 4)- 2 : (a2)- 3 =
c) (x4) : (x2)5 = c) ((- 3)2)2 . (- 4)2 =
d) ((n3)2)8 = d) (xm)3 : xm =
e) (2a4) . (a2)4 = e) (x2)n : (xn)3 =
4. Potenciranje produkta
Pravilo: ( a . b )n = an . bn
1) 2) 3) 4) Skrči :
a) ( 3x)5= a) (- 4x2y)3= a) – 42 = a) 5a2b +7 a2b =
b) (- 2y)4= b) (- 3x - 2)3= b) (- 4)2 = b) 6xy –6xy2 +2xy =
c) ( - 3b)3= c) (5a- 3b)- 2= c) 4(a2)3. 2(b2)3 = c) 7x3- 2x – 6x3 =
d) (5x4)3= d) 3(x4)2 = d (4a2)3. (2b2)3 = d) 7x3 –6x2 –4x3 – x2 =