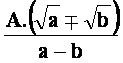Pri potenciranju b n = a iščemo iz znane osnove b in iz znanega eksponenta n potenco a.
Možni sta dve obratni operaciji:
a) iz znane potence a in iz znanega eksponenta n iščemo osnovo b; to operacijo imenujemo korenjenje;
b) iz znane potence a in iz znane osnove b iščemo potenčni eksponent n; to operacijo imenujemo logaritmiranje.
Najprej bomo proučili korenjenje:
bn = a
b = ![]()
Iskati osnovo b iz znane potence a in iz znanega eksponenta n pomeni, iskati tisto število b, katerega n-ta potenca je število a.
Potenco a imenujemo korenjenec ali radikand, eksponent n korenski eksponent, iskano osnovo b pa koren.
Dogovor:
![]()
Osnovne lastnosti korenov
![]() = a in
= a in ![]() = a
= a
![]()
Krajšanje in razširjanje korenov
Koren ne spremeni svoje vrednosti, če korenski eksponent in potenčni eksponent korenjenca množimo ali delimo z istim številom.
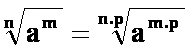
Računske operacije s koreni
1. SEŠTEVANJE IN ODŠTEVANJE
Seštevamo in odštevamo le korene, ki imajo enake radikande in enake korenske eksponente, in sicer po pravilu za seštevanje oziroma odštevanje enočlenikov.
a . ![]() ± b .
± b . ![]() = ( a ± b ) .
= ( a ± b ) . ![]()
Če omenjena pogoja nista izpolnjena, ostane seštevanje oziroma odštevanje le nakazano.
2. MNOŽENJE KORENOV
A) Z ENAKIMI KORENSKIMI EKSPONENTI
Korena z enakima korenskima eksponentoma množimo tako, da korenimo produkt radikandov z enakim korenskim eksponentom.
![]() .
. ![]() =
= ![]()
Dokaz:
Za dokaz zapišemo:
![]() =u ,
=u , ![]() = v ali a = un , b = vn
= v ali a = un , b = vn
Napravimo produkt: a . b = ( un . vn ) = ( u . v)n
Iz tega sledi: u . v =
![]() ali
ali ![]() .
. ![]() =
= ![]()
B) Z RAZLIČNIMI KORENSKIMI EKSPONENTI
Korene, ki nimajo enakih korenskih eksponentov, najprej pa pravilu o razširjenju korenov pretvorimo na najmanjši skupni korenski eksponent.
Pravilo za množenje korenov v obratni smeri:
n–ti koren produkta je produkt n–tih korenov posameznih faktorjev.
![]() =
= ![]() .
. ![]()
Pri n-tem korenu produkta lahko tiste faktorje, ki so n-te potence, korenimo in rezultate tega korenjenja postavimo kot faktorje pred koren. To operacijo imenujemo delno korenjenje.
3. DELJENJE KORENOV
A) Z ENAKIMI KORENSKIMI EKSPONENTI
Korena z enakima korenskima eksponentoma delimo tako, da kvocient radikandov korenimo z enakim korenskim eksponentom.
![]() :
: ![]() =
= ![]()
Za dokaz zapišemo:
![]() =u ,
=u , ![]() = v ali a = un , b = vn
= v ali a = un , b = vn
Količnik
![]() ,od tod je
,od tod je ![]() ali
ali ![]()
B) Z RAZLIČNIMI KORENSKIMI EKSPONENTI
Če korena nimata enakih korenskih eksponentov, ju pretvorimo na najmanjši skupni korenski eksponent.
V obratni smeri se pravilo za deljenje korenov glasi:
n -ti koren ulomka je ulomek, katerega števec je n-ti koren števca, imenovalec pa n-ti koren imenovalca.
![]() =
= ![]()
3. POTENCIRANJE KORENOV
Koren potenciramo z nekim številom tako, da s številom potenciramo radikand, dobljeno potenco pa korenimo s korenskim eksponentom.
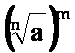 =
= ![]()
Dokaz:
![]() =
= ![]() .
. ![]() .
. ![]() .
. ![]() . . .
. . . ![]() =
= ![]() =
= ![]()
m – faktorjev m – faktorjev
V obratni smeri se pravilo za potenciranje korena glasi:
Potenco korenimo tako, da korenimo njeno osnovo, dobljeni koren pa potenciramo s potenčnim eksponentom.
![]() =
= ![]()
Dovoljena je zamenljivost vrstnega reda potenciranja in korenjenja.
4. KORENJENJE KORENOV
Koren korenimo tako, da korenimo radikand s produktom obeh korenskih eksponentov.
![]()
![]()
Dokaz:
Za dokaz pišimo: a = u m . n
ali u = ![]()
Potem je:
![]()
![]() =
= ![]() = u =
= u = ![]()
Pravilo za korenjenje korena se obratno glasi:
Število korenimo s produktom dveh števil tako, da ga korenimo najprej s prvim faktorjem, dobljeni koren pa še z drugim faktorjem.
![]() =
= ![]()
Ker je m . n = n . m velja:
![]() =
= ![]() ali
ali ![]() =
= ![]()
Pri korenjenju korena smemo zamenjati vrstni red obeh korenjenj.
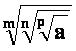 =
= ![]()
5. KORENI KOT POTENCE, KATERIH EKSPONENT JE ULOMEK
(POTENCE Z RACIONALNIMI EKSPONENTI)
Število potencirati z ulomkom pomeni, potencirati ga s števcem in koreniti z imenovalcem.
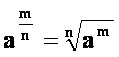
Vsak koren moramo pisati kot potenco, katere eksponent je ulomek: njegov števec je potenčni eksponent radikanda, imenovalec pa je korenski eksponent.
![]() =
= ![]()
6. RACIONALIZACIJA IMENOVALCEV
Odpravljanje korena iz imenovalca imenujemo racionalizacija imenovalca.
1. primer:
![]()
Če števec in imenovalec pomnožimo z
![]() , dobimo:
, dobimo:
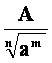 =
= 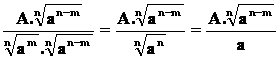
V imenovalcu sedaj ni korena.
2. primer:
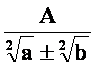
Števec in imenovalec pomnožimo z razliko
oziroma vsoto ![]() .
.
![]() =
= 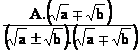 =
=