Pojem spremenljivke
Spremenljivka x je znak za več različnih števil. Konstanta a je znak za eno samo določeno število. Število vrednosti, ki jih more spremenljivka x zavzeti, je lahko končno ali neskončno. Če je x vsako realno število med realnima številoma a in b, pravimo, da je x zvezna realna spremenljivka v intervalu a in b.
To zapišemo v obliki a £ x £ b, pri pogoju a < b in da spadata a in b k intervalu. Tak interval imenujemo zaprti interval. Intervala a < x £ b in a £ x < b sta delno zaprta, interval a < x < b je odprti interval. Domenimo se za način pisave:
Neskončni interval( poltrak) {x; x ³ a} bomo pisali kot [a, ¥ ); poltrak
{x; x > a} bomo pisali kot (a, ¥ ). Ležečo osmico preberemo kot » neskončno«. Podobno je:
{x; x £ b } pišemo kot ( - ¥, b ]
{x; x < b } pišemo kot ( - ¥, b )
|
a |
|
a |
|
a |
|
a |
|
b |
|
b |
|
b |
|
b |
|
0 |
|
0 |
|
0 |
|
0 |
|
x |
|
x |
|
x |
|
x |
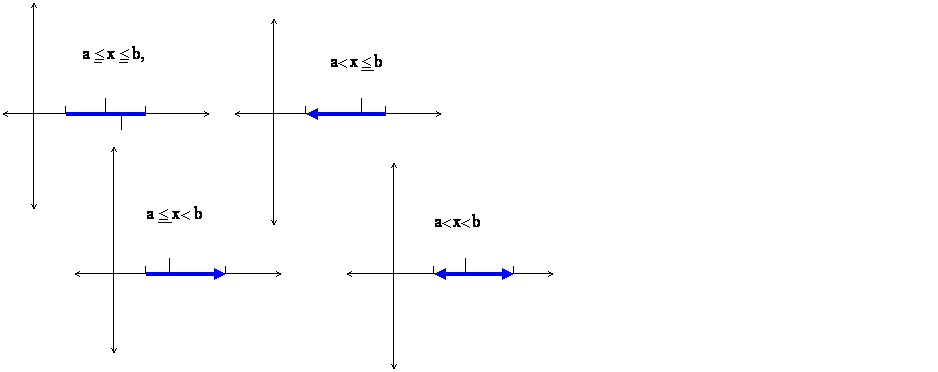Celo
realno os včasih zapišemo kot ( - ¥, ¥ ).
zaprti interval delno odprti
delno odprti odprti interval
|
0 |
|
0 |
|
0 |
|
a |
|
b |
|
x |
|
x |
|
x |
poltrak poltrak
realna os
Zvezno spremenljivko x si lahko predstavljamo kot točko, ki se giblje po številski premici. Če se giblje vedno v isti smeri, je monotona spremenljivka. Če se giblje stalno v desno smer, je monotono naraščajoča spremenljivka, če pa stalno proti levi, je monotono pojemajoča spremenljivka.
Primeri za spremenljivke so nam že poznani.
Iz geometrije: če pomislimo na različne daljice, kvadrate, kroge itd., so spremenljivke dolžina daljice, stranica, obseg, diagonala, ploščina kvadrata, obseg in ploščina kroga…
Iz fizike: čas, pot, hitrost, pospešek, jakost sile, temperatura, prostornina plina itd.
Spremenljivke označujemo navadno z zadnjimi črkami abecede: x, y, z, u, v; konstante pa s prvimi črkami abecede: a, b, c, d…
Funkcijska zveza med spremenljivkami
Med vsaj dvema spremenljivkama je možna zveza v obliki medsebojne odvisnosti. Pravimo, da je med njima funkcijska zveza.
Primeri: dolžina kovinske palice in temperatura, ki jo ima palica, obseg in polmer kroga, ploščina in stranica kvadrata, čas in pot in hitrost itd.
Vsaki temperaturi je prirejena določena dolžina palice in obratno vsaki dolžini palice pripada določena temperatura. Enako je v drugih primerih. Značilno za funkcijsko zvezo je torej, da pripada vsaki vrednosti ene spremenljivke natančno določena vrednost druge spremenljivke.
Pojem spremenljivke
Vzemimo, da je med spremenljivkama x in y funkcijska zveza. Spremenljivki x dajmo neko prednost, in sicer tako, da jo po svoji volji spreminjamo v nekem intervalu. V tem primeru jo imenujemo neodvisno spremenljivko. Ker obstoji funkcijska zveze, se spreminja tudi y. Vsaki vrednosti x pripada zaradi funkcijske zveze med njima čisto določena vrednost y. Pravimo, da je y odvisna spremenljivka ali funkcija x.
y je funkcija x, če obstoji pravilo, ki prireja vsaki vrednosti x iz določenega intervala čisto določeno vrednost y.
Kakor vidimo je poseben poudarek na naslednjem:
a) funkcijska zveza med x in y,
b) pravilo prirejanja,
c) interval za neodvisno spremenljivko x.
Pravilo prirejanja
To pravilo je lahko zelo različno. Navadno je v obliki enačbe med x in y. Zapisi so: y = ax + b, y = ax2 + bx + c, s = v . t , Q = c.m ( T2 – T1) itd.
Pravilo je lahko povedano tudi samo z besedami.
Če se povečamo prvo količino enkrat, dvakrat, trikrat… se poveča tudi druga količina enkrat, dvakrat, trikrat...
Pravilo je lahko zapisano tudi v obliki tabele. Npr, nasičenost vlage v zraku pri določeni temperaturi
Pravilo je lahko dano tudi s krivuljo v danem koordinatnem sistemu.Abcise točk na krivulji so vrednosti neodvisne spremenljivke, pripadajoče ordinate pa vrednosti funkcije. Take krivulje rišeta termograf , barograf, osciloskop…
Interval za neodvisno spremenljivko
Interval za neodvisno spremenljivko lahko razberemo iz enačbe, če je dana funkcija z enačbo.
Pri
funkciji y = 2x + 4 je interval za x: - ¥ < x < ¥ ; pri funkciji y = 1/x je
interval isti vendar moramo izključiti 0; pri funkciji y =
je interval za x:
0 £ x < ¥.
Slika: interval
interval
Včasih moramo interval določiti smiselno. Obrazec za pot enakomernega gibanja s hitrostjo v se glasi s = v . t ali s je funkcija t. Po enačbi bi bil interval za t:
- ¥ < t < + ¥. Smiselno je pa le od trenutka, ko se gibanje začne, do trenutka, ki ga hočemo.
Označba funkcije
Če je y funkcija x, zapišemo to v obliki y = f(x) in govorimo: y je funkcija x. Če imamo več funkcij, uporabljamo še označbe F(x), g(x), G(x), f1(x), f2(x) itd.
Vrednost funkcije f(x) za vrednost x0 imenujemo funkcijsko vrednost v x0 in jo pišemo f(x0) in izgovorimo: f v x0.
Geometrična ponazoritev funkcije
Izberemo poljubne vrednosti x in jim iz enačbe, ki definira funkcijo, izračunamo y. Dvojice (x, y) označimo kot točke v pravokotnem koordinatnem sistemu. Te točke se dajo v splošnem zvezati s krivuljo, ki je slika, grafikon ali diagram funkcije.
Eksplicitne in implicitne funkcije
Če je y kot funkcija x dana v obliki take enačbe, da je na eni strani samo y, na drugi strani pa izraz zx, potem imenujemo tako funkcijo razvito ali eksplicitno funkcijo; v nasprotnem primeru pa jo imenujemo nerazvito ali implicitno obliko.
Primeri eksplicitnih funkcij: y = kx + n, y = ax2 + bx + c, y = sin x itd.
Primeri inplicitnih funkcij: x2 + y2 = r2, ax + by + c = 0,
cos x + sin y = 1 itd.
Iz implicitne oblike dobimo eksplicitno, če enačbo, ki podaja funkcijsko zvezo, razrešimo, če se da, na spremenljivko, ki jo smatramo za funkcijo.
Naraščajoče in padajoče funkcije
Ko se vozimo z avtomobilom, število prevoženih kilometrov na števcu narašča, hkrati pa tudi narašča količina porabljenega goriva, zaloga goriva v rezervoarju pa pada.
Če se potapljamo pritisk narašča z globino, količina svetlobe pa pada z globino.
Če imamo funkcijo y = f(x) bi lahko rekli, da funkcija f(x) narašča, če se njene vrednosti večajo, ko se veča spremenljivka x in funkcija f(x) pada, če se njene vrednosti manjšajo, ko se spremenljivka x veča.
Matematični zapis tega pojava je:
Funkcja f narašča, če za, x2 > x1 sledi f(x2) > f(x1) za poljubna x1 , x2 na danem intervalu.
Primer:
F(x) = 2x je naraščajoča funkcija na celi realni osi.
Namreč, če je x2 > x1 je 2x2 > 2x1 , saj smemo neenakost pomnožiti s pozitivnim celim številom.
|
x |
|
x |
|
1 |
|
2 |
|
f(x1)
|
|
f(x2) |
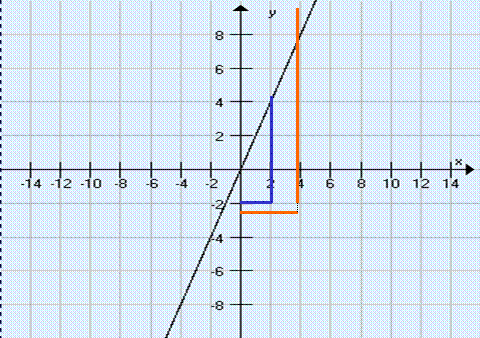Na
enak način dokažemo da je funkcija f(x) = kx naraščajoča, če je k
> 0.
Na grafu funkcije se naraščanje pozna takole: če se gibljemo s spremenljivko x proti desni ( v smeri naraščanja spremenljivke x), se večajo tudi vrednosti f(x); točke na grafu funkcije se pomikajo navzgor.
Funkcija f pada, če za x2 > x1 sledi f(x2) < f(x1) za poljubna x1 , x2 na danem intervalu.
F(x) = - 2x je padajoča funkcija na celi realni osi.
Namreč, če je x2 > x1 je 2x2 < 2x1 , saj se znak neenakosti obrne, če pomnožimo z negativnim celim številom.
Na enak način dokažemo da je funkcija f(x) = kx padajoča, če je
k < 0.
|
f(x2) |
|
f(x1) |
|
x |
|
x |
|
1 |
|
2 |
Na grafu funkcije se padanje pozna takole: če se gibljemo s spremenljivko x proti desni ( v smeri naraščanja spremenljivke x), se manjšajo vrednosti f(x); točke na grafu funkcije se pomikajo navzdol.
Sodost in lihost funkcije
Funkcija f je soda, če velja f(x) = f(-x) za vsak x z njenega definicijskega območja. Če je točka T1(x, f(x)) na grafu take funkcije je tudi točka T2( - x, f(x)) na tem grafu.
Sodi funkciji sta: f(x) = ô x ô, f(x) = x2, f(x) = x4… f(x) = x2 n
Na grafu funkcije se sodost pozna takole: Točki T1 in T2 ležita simetrično glede na ordinatno os. Zato graf sode funkcije narišemo najprej desno od ordinatne osi. Nato prezrcalimo narisano čez ordinatno os, pa imamo celoten graf.
Zgleda : 1) f(x) = ô x ô, saj je ô - x ô= ô x ô
Tabela:
|
X |
- 4 |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
|
I x I |
4 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
2) f(x) = x2 in f( - x) = ( - x )2 = x2 ž
Tabela:
|
X |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
X 2 |
|
|
|
0 |
1 |
4 |
9 |
16 |
|
T |
|
T |
|
1 |
|
2 |
|
x |
|
- x |
|
( - x, y ) |
|
( x, y )) |
|
T |
|
T |
|
1 |
|
2 |
|
T |
|
T |
|
1 |
|
2 |
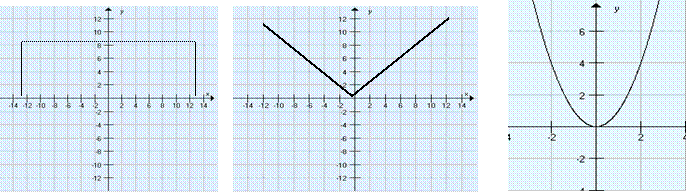
Simetrično ležeči točki f(x) = IxI f(x) = x2
T1 in T2 glede na ordinatno os.
Funkcija f je liha , če velja f( - x) = - f(x) za vsak x z njenega definicijskega območja. Če je (x, f(x)) točka na grafu lihe funkcije, je tudi ( -x, -f(x)) točka na tem grafu. Točki T1 in T2 ležita simetrično na izhodišče koordinatnega sistema.
Lihe funkcije so: f(x) = x, f(x) = x3, f(x) = x5…f(x) = x2 n+1
Na grafu funkcije se lihost pozna takole:Točki T1 in T2 ležita simetrično glede na koordinatno izhodišče. Običajno graf lihe funkcije narišemo najprej na intervalu [0, ¥ ), nato pa narisano zavrtimo za 1800 okrog izhodišča (prezrcalimo čez izhodišče), pa imamo narisan celoten graf f.
Zgleda: 1) f(x) = x saj je f(-x) = -x
Tabela:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
f(x) |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
2) f(x) = x3 saj je f(-x) = (-x)3 = -x3
Tabela:
|
x |
0 |
|
|
|
1 |
|
2 |
3 |
4 |
|
X3 |
0 |
|
|
|
1 |
|
8 |
27 |
64 |
|
T |
|
T |
|
1 |
|
2 |
|
(x , y) |
|
( - x , - y ) |
|
1 |
|
2 |
|
T |
|
T |
|
T |
|
T |
|
1 |
|
2 |
Točki T in T ležita simetrično f(x) = x f(x) = x3glede na izhodišče.
Monotone, periodične in sestavljene funkcije
Če funkcija na danem intervalu ves čas narašča ali ves čas pada, pravimo, da je monotona na tem intervalu.
Taki funkciji sta f(x) = x in f(x) = - x na celotni realni osi. Tudi funkcija f(x) = x2 je monotona na intervalu (¥ >x > 0 ) in na intervalu ( 0 >x > - ¥ ). Ni pa monotona na celotni realni osi ( ¥ > x > - ¥ ).
Funkcije, pri katerih se vse funkcijske vrednosti v enakih presledkih neodvisne spremenljivke ponavljajo, imenujemo periodične funkcije.
To zapišemo f(x +a) = f(x), kjer je a perioda funkcije. Take funkcije so f(x) = sin x,
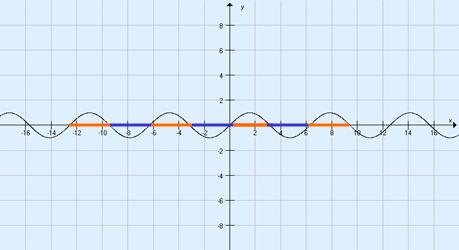f(x)
= cos x in še mnoge druge.
Zgled: f(x) = sin x
f(x) = sin x
Če je funkcija odvisna od funkcije, jo imenujemo funkcijo funkcije ali sestavljeno funkcijo.
Take funkcije so: f(x) = u2, u = ax + b y = sin v2,
v = 2x y = 
, u = x2 + x +1
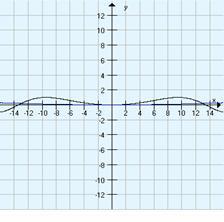
Zgled: f(x) = sin v2 ,v = 2x Þ f(x) = sin 4x2
f(x) = sin 4x2
Enolične in dvolične funkcije
Če je pravilo tako, da prireja vsaki vrednosti x iz nekega intervala eno in samo eno vrednost y, imenujemo y enolično funkcijo x; ako pa prireja vsaki vrednosti x iz nekega intervala po dve vrednosti y, je funkcija dvolična. Imamo tudi mnogolične funkcije.
Funkcije, ki niso definirane v točki 0
Če si ogledamo funkcijo f(x) = x –n in je (nÎN)
In njen najpreprostejši primer n = - 1 dobimo funkcijo
f(x) = x - 1 ali f(x) =
Narišimo si tabelo in upoštevajmo, da je funkcija liha.
|
x |
|
|
|
1 |
|
2 |
3 |
4 |
|
|
4 |
2 |
|
1 |
|
|
|
|
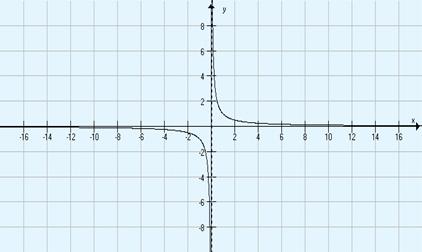
f(x)
= x - 1
Ko x potuje po pozitivnem poltraku v desno, se graf približuje osi x in ji pride poljubno blizu. Pravimo, da se graf asimptotsko bliža osi x ali da je os x asimptota grafa. Ko se x približuje točki 0, se graf asimptotsko bliža osi y.
Če se bližamo točki 0 z leve, vrednosti f(x) težijo k vrednosti - ¥ .
Oglejmo si še graf f(x) = x –2 ali f(x) =
Upoštevajmo, da je funkcija soda. Napravimo si tabelo:
|
X |
|
|
|
1 |
|
2 |
3 |
4 |
|
X – 2 |
16 |
4 |
|
1 |
|
|
|
|
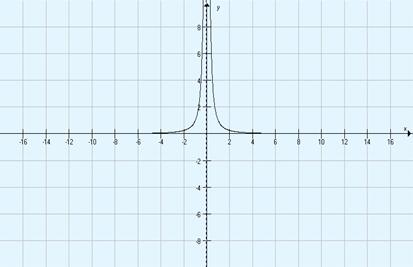
Tudi tu se graf funkcije asimptotsko bliža osema x in y. Za x < 0 funkcija narašča, za x > 0 pa pada. Namesto, da rečemo funkcija f(x) = x –2 ima v točki x = 0 vertikalno asimptoto, rečemo, da je 0 pol te funkcije.
Inverzna funkcija
Inverzno funkcijo dobimo, če spremenljivki x in y zamenjamo.
y = f(x) in x = f(y) sta inverzni funkciji. Dobljena grafa ležita simetrično glede na premico y = x
Na grafu funkcije se inverzija pozna takole:
Točki T1( x, y) in T2( y, x) ležita simetrično glede na simetralo y = x.
Graf inverzne funkcije dobimo tako da graf za f prezrcalimo, čez simetralo y = x.
Zgled: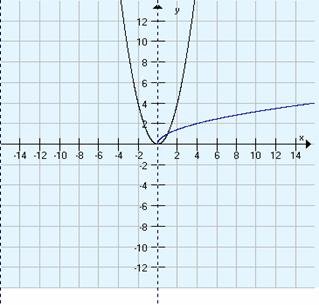
y = x2 in x = y2 . Načrtali bomo torej
funkciji y = x2 in y = 
.Ker kvadratnih korenov negativnih števil ni na realni osi
bo dovolj, če preslikamo le vrednosti funkcije y = x2 , kjer je x >
0.
f(x) = x2
in f(x) =
Definicijsko območje funkcije [ 0, ¥ ) je in tudi zaloga vrednosti je tudi [ 0, ¥ ).
Funkcija je naraščajoča.
Pojem zveznosti funkcije
Geometrično pomeni, da je funkcija zvezna v intervalu, da ni krivulja, ki funkcijo predočuje, nikjer pretrgana. Funkcija y = x je za vsako vrednost x zvezna. Funkcija
y =
je za x = 0 nezvezna.
Načrtanih je še nekaj funkcij: oglej si
njihovo naraščanje, padanje,sodost in lihost.
