Naloge z napako

1. V trikotniku \(\triangle ABC\) je stranica \(b\) za 20% krajša od stranice \(a\), stranica \(c\) pa je dvakrat daljša od stranice \(a\), Izračunaj stranice tega trikotnika, če veš, da obseg trikotnika meri \(57~\mathrm{cm}\).
   
   Uradna rešitev:   \(a=15~\mathrm{cm},~ b=12~\mathrm{cm},~ c=30~\mathrm{cm}\)
   Napaka:
   Trikotnik s takimi stranicami ne obstaja, ker je stranica \(c\) tako dolga, da ostalih dveh stranic ne moremo sestaviti skupaj.
   To pomeni, da ni izpolnjena trikotniška neenakost \(c\lt a+b\).
   
   Pri danem besedilu naloge se pravilni odgovor glasi:
   Naloga nima rešitve – tak trikotnik ne obstaja.
2. Dolžine stranic v \(n\)-kotniku sestavljajo končno geometrijsko zaporedje s količnikom \(k=3\). Najkrajša stranica meri \(5~\mathrm{cm}\), obseg tega \(n\)-kotnika pa meri \(1820~\mathrm{cm}\). Določi število \(n\) in izračunaj dolžino najdaljše stranice.
   
   Uradna rešitev:   \(n= 6\) (to je šestkotnik),  \(a_6=1215~\mathrm{cm}\)
   Napaka:
   Če izračunamo vrednosti vseh členov ustreznega geometrijskega zaporedja (5, 15, 45, 135, 405, 1215), hitro vidimo, da bi morala biti najdaljša stranica dosti daljša kot vse ostale stranice skupaj. Podobno kot v prejšnji nalogi lika s takšnimi stranicami ne moremo sestaviti.
   
   To je posledica količnika \(k=3\). Stranice večkotnika nikoli ne morejo sestavljati geometrijskega zaporedja s količnikom \(k\geqslant 2\), saj bi bila najdaljša stranica v tem primeru predolga.
   (Mimogrede: tudi \(k\leqslant\frac{1}{2}\) ni v redu.)
   
   Pri danem besedilu naloge se pravilni odgovor glasi:
   Naloga nima rešitve – tak večkotnik ne obstaja.
3. Izračunaj največji skupni delitelj in najmanjši skupni večkratnik števil  \(a=n^2+n\)  in  \(b=n^2-n\).
   
   Uradna rešitev:   \(D=n,~ v=n(n+1)(n-1)\)
   Napaka:
   Prva napaka je pomanjkljivo izražanje.
   V besedilu naloge ne piše, v okviru katere množice je treba računati. Privzemimo, da gre za deljivost v množici celih števil \(\mathbb{Z}\).
   
   Poglejmo še drugo (hujšo) napako.
   Z razcepom dobimo \(a=n(n+1)\) in \(b=n(n-1)\). Očitno je \(n\) skupni delitelj, vendar pa to ni nujno največji skupni delitelj. Če je spremenljivka \(n\) liho število, sta faktorja \(n+1\) in \(n-1\) sodi števili in imata skupni delitelj 2.
   
   Pravilni odgovor je torej daljši in ima dve varianti:
   Če je \(n\) sodo število, velja:  \(D=n,~ v=n(n+1)(n-1)\);
   če je \(n\) liho število, potem pa velja:  \(D=2n,~ v=\frac{1}{2}n(n+1)(n-1)\).
4. Dokaži, da za vsak \(x\in\mathbb{R}\) velja:   \(\displaystyle\frac{x-\frac{1}{x}}{1-\frac{1}{x}}-x = 1\)
   
   Uradna rešitev:   Enakost res velja za za vsak \(x\in\mathbb{R}\).
   Napaka:
   Preoblikujmo izraz na levi strani:

   \(\displaystyle\frac{x-\frac{1}{x}}{1-\frac{1}{x}}-x \) \(\displaystyle =\frac{~\frac{x^2-1}{x}~}{\frac{x-1}{x}}-x = \)

   \(\displaystyle =\frac{x^2-1}{x-1}-x \) \(\displaystyle =\frac{(x-1)(x+1)}{x-1}-x = \)

   \(=(x+1)-x \) \(=1\)

   Tako vidimo, da je vrednost danega izraza res vedno enaka 1.
   Vedno?
   Pravzaprav ne: če poskusimo v prvotni izraz vstaviti \(x=0\) ali \(x=1\), hitro vidimo, da vrednost izraza ni enaka 1, pač pa je nedefinirana zaradi deljenja z 0.
   
   Napaka je torej v besedilu naloge.
   Namesto „Dokaži, da za vsak \(x\in\mathbb{R}\) velja”, bi moralo pisati:
   Dokaži, da enakost velja za vsak \(x\in\mathbb{R}\), za katerega je izraz na levi definiran.
   Ali pa morda bolj konkretno:
   Dokaži, da enakost velja za vsak \(x\in\mathbb{R}\setminus\{0,~1\}\).
5. Dokaži, da ima dana enačba za vsak \(m\in\mathbb{R}\) dve različni realni rešitvi:   \(\displaystyle x^2-3x=\frac{2x^2-18}{m+2}\)
   
   Uradna rešitev:   Enačba ima rešitvi \(x_1=3\) in \(x_2=\frac{6}{m}\).
   Napaka:
   Poskusimo rešiti enačbo. Najprej odpravimo ulomek in uredimo člene:
       \(mx^2-(3m+6)x+18=0\)
   
   Izračunamo diskriminanto \(D=(3m-6)^2\) in rešitvi:
       \(x_1=3,~ x_2=\frac{6}{m}\)
   
   Na prvi pogled se zdi, da ima enačba res vedno dve rešitvi. Podrobnejši pregled pa nam pokaže nekaj izjem:

   • Če je \(m=-2\), enačba sploh ne obstaja (ni smiselna), saj v imenovalcu desne strani enačbe nastopa 0. Desna stran enačbe torej ni definirana.
   • Če je \(m=2\), je diskriminanta kvadratne enačbe enaka 0, zato ima enačba eno samo rešitev. Izračunani vrednosti \(x_1\) in \(x_2\) predstavljata isto rešitev, saj velja: \(x_2=\frac{6}{2}=3=x_1\).
   • Če je \(m=0\), pa dana enačba sploh ni kvadratna enačba. V tem primeru je enačba linearna \((3x=9)\) in ima eno samo rešitev \((x=3)\).

   Besedilo naloge bi se moralo glasiti:
   Dokaži, da ima dana enačba za vsak \(m\in\mathbb{R}\setminus\{-2,~ 0,~ 2\}\) dve različni realni rešitvi.
6. Poišči realno število \(x\), za katero velja:   \(\sqrt{x^2-5x}=\sqrt{5x-9}\)
   
   Uradna rešitev:   \(x=9\)
   Napaka:
   Poskusimo rešiti enačbo. Najprej odpravimo oba korena in uredimo člene:
       \(x^2-10x+9=0\)
   
   Ta enačba ima dve realni rešitvi:
       \(x_1=9,~ x_2=1\)
   
   Zdaj naredimo preizkus:

   • Za \(x_1=9\) dobimo na obeh straneh enačbe isto vrednost \(\sqrt{36}=6\). Preizkus velja in število \(x_1=9\) je rešitev dane enačbe.
   • Za \(x_2=1\) dobimo na obeh straneh enačbe isto vrednost \(\sqrt{-4}=2i\). Preizkus tudi v tem primeru velja in tudi število \(x_2=1\) je rešitev dane enačbe.

   Problem pri tej nalogi je vprašanje, če je prav, da v drugem preizkusu uporabimo kompleksna števila. V besedilu naloge piše, da mora biti \(x\) realno število, nič pa ne piše o preizkusu. Če se strogo držimo besedila, je \(x_2=1\) tudi rešitev dane enačbe.
   
   Vendar pa je tako tolmačenje zelo enostransko in ozkogledo.
   Resnični problem je vprašanje, ali naslednji dve navodili pomenita isto:
    – V množici \(\mathbb{R}\) reši enačbo…
    – Poišči realno število \(x\), za katero velja…
   
   Navodilo „V množici \(\mathbb{R}\) reši enačbo” pomeni, da morajo vsi računi (pri reševanju in pri preizkusu enačbe) potekati v množici \(\mathbb{R}\).
   Drugo navodilo govori samo o realnosti števila \(x\). To navodilo ni dovolj natančno. Problem naloge torej ni v uradni rešitvi, pač pa v uradnem besedilu, ki ni dovolj natančno.
   
   Sklep: Napaka se skriva v besedilu naloge. Besedilo bi se moralo glasiti:
   V množici \(\mathbb{R}\) reši dano enačbo.
   (In uradna rešitev je potem pravilna: \(x=9\).)
7. Pravilna pokončna prizma ima za osnovno ploskev večkotnik z obsegom \(128~\mathrm{cm}\) in s ploščino \(1230~\mathrm{cm}^2\). Višina te prizme meri \(20~\mathrm{cm}\). Izračunaj prostornino in površino te prizme.
   
   Uradna rešitev:   \(V=24\,600~\mathrm{cm}^3,~ P=5\,020~\mathrm{cm}^2\)
   Napaka:
   Poskusimo ugotoviti število stranic (\(n\)) osnovne ploskve.
   
   Iz obsega lahko določimo, koliko meri stranica \(a\) za različne vrednosti števila \(n=3,4,5,6,\ldots\)
   S tako dobljeno stranico \(a\) lahko potem izračunamo ploščino osnovne ploskve (\(S\)) in dobimo naslednje rezultate:
      \(\begin{array}{c|c|c} ~n~ & a & S \cr\hline 3 & 42.7 & 788.3 \cr 4 & 32.0 & 1024.0 \cr 5 & 25.6 & 1127.5 \cr 6 & 21.3 & 1182.4 \cr 7 & 18.3 & 1215.1 \cr 8 & 16.0 & 1236.1 \cr 9 & 14.2 & 1250.4 \end{array}\)
   Kot vidimo, ploščine sestavljajo rastoče zaporedje, vendar pa v tem zaporedju ne nastopa ploščina \(1230~\mathrm{cm}^2\). Osnovna ploskev torej ni niti sedemkotnik niti osemkotnik, pač pa bi morala biti „nekaj vmes” – kar seveda ni možno.
   
   Pri danem besedilu naloge se pravilni odgovor glasi:
   Naloga nima rešitve – taka prizma ne obstaja.
8. Pokončna piramida ima za osnovno ploskev romb z diagonalama \(e=24~\mathrm{cm},~ f=10~\mathrm{cm}\). Višina te piramide meri \(v=17~\mathrm{cm}\). Izračunaj prostornino in površino te piramide.
   
   Uradna rešitev:   \(V=680~\mathrm{cm}^3,~ P=578~\mathrm{cm}^2\)
   Napaka:
   Problem pri tej nalogi je definicija pojma „pokončna piramida”.
   V starejših učbenikih in priročnikih je pokončna piramida definirana kot piramida, ki ima vse stranske robove enako dolge. Piramida, ki ima za osnovno ploskev romb, po tej definiciji sploh ne more biti pokončna, saj ima vedno dva daljša in dva krajša stranska robova.
   Če upoštevamo to definicijo, potem se pravilni odgovor glasi:
   Naloga nima rešitve – pokončna piramida s tako osnovno ploskvijo ne obstaja.
   
   Dejansko pa je zgoraj opisana definicija problematična. Zato avtorji novejših učbenikov definicijo pokončne piramide pogosto kar izpustijo in se pretvarjajo, da pokončnost ni nekaj, kar bi nas pri piramidah zanimalo.
   
   Ali obstaja boljša definicija pokončnosti? Fizikalno in po zdravi pameti bi bila ustrezna naslednja definicija: Piramida je pokončna, če leži spodnje krajišče višine v težišču osnovne ploskve.
   Če bi veljala ta definicija, potem bi bila uradna rešitev pravilna.
   Žal te definicije ne najdemo v matematični literaturi.
9. Dana je funkcija \(f(x)=2\sin\frac{x}{2}\).
   

   (a)   V spodnji koordinatni sistem nariši graf te funkcije.

   (b)   Izračunaj kot, ki ga oklepata graf funkcije in abscisna os.

   
   Uradna rešitev:   (b)  \(\varphi=45^\circ\)
   Napaka:
   Napaka pri tej nalogi je nepravilno narisan koordinatni sistem.
   
   Rezultat \(\varphi=45^\circ\) je izračunan pravilno. Če pa graf narišemo v dani koordinatni sistem, narisani kot ne meri \(45^\circ\). Namesto tega vidimo na sliki precej večji kot (približno \(57.5^\circ\)):
   
   
   
   Žal avtorji matematičnih nalog vse prepogosto pozabljajo, da veliko postopkov in formul velja samo v koordinatnem sistemu, ki ima na obeh koordinatnih oseh enako velike enote (glej: Standardni in nestandardni koordinatni sistem).
   
   Popravimo torej enote. Če so enote na obeh oseh enake, mora biti \(\pi\doteq3.14\) enot. V takem koordinatnem sistemu je kot med grafom in vodoravno osjo res \(45^\circ\):
   
   
   
   
10. Dana je funkcija \(\displaystyle f(x)=\frac{x-2}{x-1}\). Pokaži, da funkcija \(f\) narašča za vsak \(x\ne1\).
    
    Uradna rešitev:   Odvod je enak \(f'(x)=\frac{1}{(x-1)^2}\) in je pozitiven za vsak \(x\ne1\).
    Napaka:
    Napaka pri tej nalogi je nerazumevanje definicije naraščanja.
    
    Marsikdo misli, da funkcija narašča tam, kjer je odvod pozitiven.
    Dejansko je naraščanje povezano s pozitivnim odvodom, vendar pa je za pravilni odgovor treba upoštevati tudi definicijo naraščanja.
    
    Definicija:
    Funkcija \(f\) na množici \(\mathcal{M}\) narašča, če za poljubni števili \(x_1, x_2 \in \mathcal{M}\) velja:
        \(x_1\lt x_2 \Longrightarrow f(x_1)\lt f(x_2) \)
    
    Z drugimi besedami: funkcija narašča, če ima pri večjem \(x\) tudi večjo funkcijsko vrednost \(f(x)\). In to mora veljati na celotni množici \(\mathcal{M}\).
    
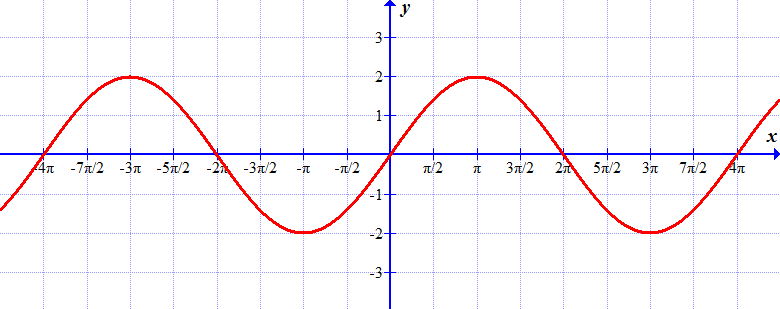
    Poglejmo si graf dane funkcije:
    
    
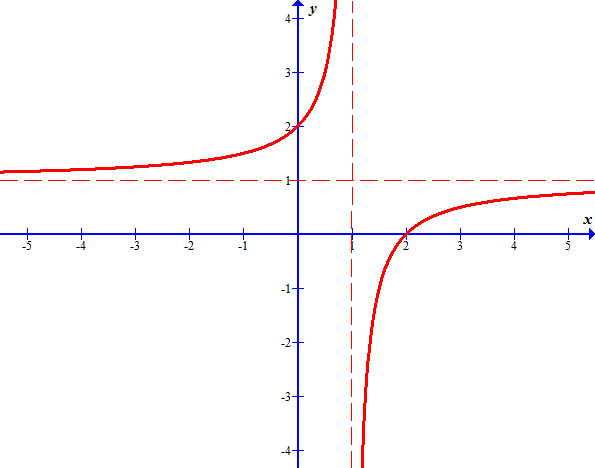
    Kot hitro vidimo, za množico \(\mathcal{M}=\{x\in\mathbb{R};~ x\ne1\}\) definicijski pogoj ne velja. Če izberemo (npr.) \(x_1=-1,~ x_2=2\), potem je pri večjem \(x\) funkcijska vrednost manjša. Torej funkcija ne narašča na celotni množici \(\mathcal{M}\).
    Funkcija pa vsekakor narašča na intervalu levo od pola. Prav tako narašča tudi na intervalu desno od pola. Pozorni moramo biti samo na dejstvo, da funkcija ne narašča na sestavljeni množici.
    
    Popravimo besedilo naloge:
    Določi intervale naraščanja dane funkcije.
    Pravilni odgovor se potem glasi:
    Dana funkcija narašča na intervalu \((-\infty,1)\), pa tudi na intervalu \((1,\infty)\).
    (Opomba: nikakor pa ne na množici \(\mathcal{M}=(-\infty,1)\cup(1,\infty)\)).

 Domov