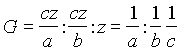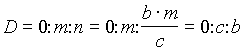
Težiščnice se sekajo v skupni točki

java applet or image

Točke D, E in F naj bodo po vrsti razpolovišča stranic BC=a, AC=b in AB=c. Označimo trilinearne koordinate točke D z 0 : m : n. Ker sta ploščini trikotnikov ABD ter CAD enaki, velja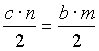 . Od tod sledi 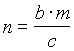. Torej je:

Analogno dobimo tudi: E = c : 0 : a ter F = b : a : 0 .

Trilinearne koordinate oglišč A, B in C so A = va : 0 : 0 = 1 : 0 : 0 ; B = 0 : 1 : 0 ; C = 0 : 0 : 1 .

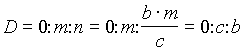
Enačba premice skozi A in D (to je nosilke težiščnice na stranico BC=a) je: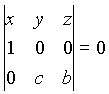 oziroma by - cz = 0

Podobno dobimo enačbo nosilke težiščnice na stranico AC=b (premica skozi B in E): ax - cz = 0 ,

nosilka težiščnice na stranico AB=c (premica skozi C in F) pa: cx - by = 0 . Te tri premice potekajo skozi skupno točko, saj zadoščajo pogoju konkurenčnosti (tri premice skozi skupno točko):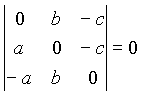

Sedaj lahko (na drug način) poiščemo še trilinearne koordinate težišča, ki smo jih že izpeljali . Rešitev sistema treh enačb težiščnic:

by - cz = 0; ax - cz = 0; ax - by = 0 je 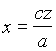, 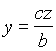. Torej je:

NAZAJ (Težišče)

Na začetno stran