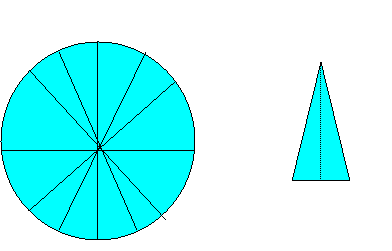
Na naslednji sliki je krogu narisanih nekaj polmerov.S tem si ga razdelil na več delov. Vsak tak del, ki ga omejujeta dva polmera in pripadajoči lok, imenujemo krožni izsek.
Vsakemu krožnemu izseku pripada lok l in središčni kot a.
krožni
izsek
Če na tak način razdeliš krog na zelo mnogo izsekov, so pripadajoči središčni koti zelo majhi in dolžina pripadajočih lokov prav tako zelo majhna, tako da se zelo malo razlikujejo od tetiv. Če je število teh izsekov zelo veliko, se skoraj ne razlikujejo od trikotnikov. Ploščino vsakega od njih lahko izračunaš po obrazcu za ploščino trikotnika.
S =
Napravil si sicer majhno napako, ki pa ostane poljubno majhna, če število izsekov bolj in bolj večaš.
Če ploščine vseh izsekov seštejemo, dobiš ploščino kroga:
S =
Vsota vseh lokov v oklepaju
je obseg kroga ali 2 .
p
.r.
l
|
l |
|
l |
|
l |
|
l |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
l |
|
r |
|
S = l . r/2 |
Torej je ploščina kroga:
Okrajšaj! 
Če upoštevaš, da je
je:
Ploščina kroga je:
ali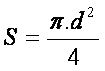 
- ploščina kroga