Realna števila

Nove množice števil uvajamo zato, da bi omogočili nove računske operacije. Tako smo uvedli cela števila zato, da smo omogočili odštevanje, racionalna števila pa zato, da smo omogočili deljenje.
Zaradi podobnega razloga uvedemo tudi realna števila.
Rešiti želimo enačbo: xⁿ = a (n ∈

, a ∈

⁺ ali tudi a ∈

⁺)
Rešitev te enačbe lahko izračunamo s korenjenjem, vendar rezultat ni vedno racionalno število. Da lahko zares korenimo, moramo uvesti množico realnih števil.

Realna števila so vsa števila, ki jih lahko zapišemo z neskončnim decimalnim zapisom.
Delijo se na racionalna in iracionalna števila:
Racionalna števila imajo periodičen (ponavljajoč) decimalni zapis, poleg tega pa jih lahko zapišemo tudi z ulomki.
Iracionalna števila imajo neperiodičen decimalni zapis (nobena skupina decimalk se ne ponavlja) in jih ne moremo zapisati z ulomki.

Množico realnih števil označimo:

Uporabljamo tudi oznaki:

⁺ = množica vseh pozitivnih realnih števil

⁻ = množica vseh negativnih realnih števil

Torej velja:

⁻ ∪ {0} ∪

⁺

Racionalna števila so podmnožica realnih, torej:

⊂

Računski zakoni

Za seštevanje in množenje v množici realnih števil veljajo naslednji zakoni oziroma aksiomi (za ∀a, b, c ∈

a + b = b + a	komutativnostni zakon (za seštevanje)
a + (b + c) = (a + b) + c	asociativnostni zakon (za seštevanje)
a + 0 = a	zakon o nevtralnem elementu (za seštevanje)
a + (−a) = 0	zakon o inverznem (nasprotnem) elementu (za seštevanje)
a b = b a	komutativnostni zakon (za množenje)
a (b c) = (a b) c	asociativnostni zakon (za množenje)
a 1 = a	zakon o nevtralnem elementu (za množenje)
a a⁻¹ = 1 (za a ≠ 0)	zakon o inverznem (obratnem) elementu (za množenje)
a (b + c) = a b + a c	distributivnostni zakon (za seštevanje in množenje)

V zgoraj zapisanih zakonih odštevanje in deljenje ne nastopata, ker odštevanje pomeni prištevanje nasprotne vrednosti (torej: a − b = a + (−b)), deljenje pa pomeni množenje z obratno vrednostjo (torej: a : b = a b⁻¹).

Računanje z realnimi števili

Realna števila imajo neskončen decimalni zapis. S tako zapisnimi števili je v praksi težko računati, zato uporabljamo naslednji dve praktični obliki zapisa:

Točno ali analitično računanje
Če želimo, da bi bil rezultat popolnoma točen, pustimo nekatere funkcije neizračunane (npr. korenjenje), za določena števila pa uporabljamo posebne oznake (npr. π).
Primeri realnih števil v točni obliki:
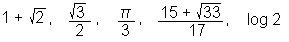
Približno ali numerično računanje
Če ne potrebujemo točnega rezultata, se lahko zadovoljimo s približkom - to pomeni, da realno število zaokrožimo. Pri tem zapišemo samo nekaj decimalnih mest, nadaljna mesta pa izpustimo. Če je prva izpuščena števka večja ali enaka 5, zadnjo še upoštevano števko povečamo za 1.
Pri zaokrožanju uporabljamo dva načina poimenovanja:
Zaokrožanje na n decimalk (decimalke so števke za decimalno vejico)
Zgled: število 12,3456789 zaokrožimo:
- na 0 decimalk:     12
- na 1 decimalko: 12,3
- na 2 decimalki:    12,35
- na 3 decimalke: 12,346
- na 4 decimalke: 12,3457
- na 5 decimalk:     12,34568

Zaokrožanje na n mest. Za mesta v zapisu števila štejemo števke pred decimalno vejico in za njo, vendar pa ne upoštevamo ničel na začetku (pred prvo od nič različno števko).
Zgledi: naslednja števila zaokrožimo na štiri mesta:
   12,34567 ≈ 12,35
   0,654321 ≈ 0,6543
   2573,333 ≈ 2573
   0,055221 ≈ 0,05522
   1578785   ≈ 1,579 ∙ 10⁶

Geometrijska ponazoritev realnih števil

Števila geometrijsko ponazorimo s točkami na številski osi. Naravna in cela števila ponazorimo s posameznimi nepovezanimi točkami. Racionalna števila pokrivajo številsko os bolj na gosto - med poljubnima dvema racionalnima številoma leži še vsaj eno racionalno število (npr. aritmetična sredina obeh danih števil). Vendar pa tudi racionalna števila ne pokrivajo vseh točk številske osi. Točke, ki ostanejo nepokrite, ustrezajo iracionalnim številom.
Realna števila popolnoma prekrivajo številsko os, tako da velja:
Vsakemu realnemu številu ustreza točno ena točka na številski osi in vsaki točki na številski osi ustreza točno eno realno število.
Drugače povedano: Preslikava, ki preslika realna števila v točke na številski osi, je povratno enolična (tj. bijektivna). Zato pravimo številski osi tudi realna os.

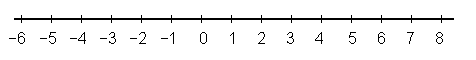
Številska os

Intervali

Interval je množica realnih števil, ki ležijo med dvema danima številoma. Glede na to, ali sta dani števili vključeni v to množico ali ne, ločimo različne vrste intervalov:

Zaprti interval vsebuje tudi obe krajišči, označimo ga [a, b], torej:
[a, b] = {x ∈

; a ≤ x ≤ b}

Odprti interval ne vsebuje krajišč, označimo ga (a, b), torej:
(a, b) = {x ∈

; a < x < b}

Polodprti interval vsebuje samo eno od krajišč, označimo ga z oglatim oklepajem pri tistem krajišču, ki ga interval vsebuje, torej:
[a, b) = {x ∈

; a ≤ x < b}
(a, b] = {x ∈

; a < x ≤ b}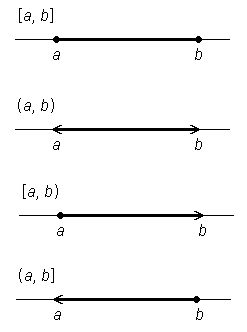

Oznake intervalov posplošimo tudi na primere, ko se eno od krajišč (ali celo obe) odmakne v neskončnost. Takim intervalom pravimo neskončni intervali. Ločimo več primerov:

[a,

) = {x ∈

; a ≤ x}

(a, neskončno

) = {x ∈

; a < x}

(− neskončno

, b] = {x ∈

; x ≤ b}

(− neskončno

, b) = {x ∈

; x < b}

(− neskončno

) =

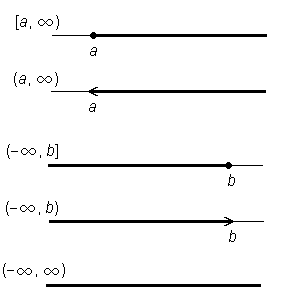
Urejenost realnih števil

Za urejenost realnih števil (po velikosti) veljajo naslednji zakoni:

Zakon trihotomije: za poljubni realni števili a in b velja točno ena od naslednjih treh možnosti:
ali je a < b ali je a > b ali pa je a = b
Zakon tranzitivnosti:
(a < b ∧ b < c) ⇒ a < c
Če neenačbi prištejemo na obeh straneh isto število, se neenakost ohrani:
a < b ⇒ a + c < b + c
Če neenačbo pomnožimo na obeh straneh z istim pozitivnim številom, se neenakost ohrani:
(a < b ∧ c > 0) ⇒ a c < b c
Če neenačbo pomnožimo na obeh straneh z istim negativnim številom, se neenačaj obrne:
(a < b ∧ c < 0) ⇒ a c > b c

Absolutna vrednost realnega števila

Absolutna vrednost realnega števila x je razdalja med točko, ki predstavlja število x, in točko, ki predstavlja število 0 na realni osi.
Oznaka: |x|

Če je število x pozitivno ali enako 0, je absolutna vrednost enaka številu samemu. Če je število x negativno, pa je absolutna vrednost enaka nasprotni vrednosti števila x.
Torej:

Lastnosti absolutne vrednosti:
|x y| = |x| |y| (absolutna vrednost produkta je enaka kot produkt absolutnih vrednosti)
|x/y|

(absolutna vrednost količnika je enaka kot količnik absolutnih vrednosti)

(Opozorilo: Za vsoto in razliko pa podoben zakon ne velja.)