Risanje trikotnik – konstrukcijske naloge

Na tej strani so predstavljei neke vrste recepti za risanje oziroma konstruiranje trikotnikov glede na dane podatke. Večino konstrukcijskih nalog za trikotnike lahko rešite s pomočjo enega od navedenih postopkov (seveda morate ustrezno prilagoditi podatke).

Za ogled datotek morate namestiti brezplačni program GeoGebra.

a) SKLADNOSTNI IZREKI

Osnovne naloge so povezane s tako imenovanimi skladnostnimi izreki, s pomočjo katerih lahko konstruiramo trikotnike, če imamo podane različne podatke o stranicah oziroma pripadajočih kotih.

a1. Načelo SSS (načelo stranica-stranica-stranica)

a2. Načelo SKS (načelo stranica-kot-stranica)

a3. Načelo KSK (načelo kot-stranica-kot)

a4. Načelo SsK (načelo večja stranica-manjša stranica-kot)

Več o skladnostnih izrekih in primere nalog si lahko ogledate na spletni strani HMTL: trikotnikSkladnost.html.

b) ZNAMENITE TOČKE

Trikotnik ima tudi nekaj znamenitih točk, s pomočjo katerih lahko rešimo nekatere geometrijske naloge. Več o znamenitih točkah trikotnika si lahko ogledate na spletni strani HMTL: trikotnikZnamTck.html.

b1. Višinska točka: Presečišče nosilk višin na stranice trikotnika.

b2. Središče trikotniku očrtane krožnice: Presečišče simetral stranic trikotnika.

b3. Središče trikotniku včrtane krožnice: Presečišče simetral kotov trikotnika.

b4. Težišče trikotnika: Presečišče težiščnic na stranice trikotnika.

c) POSEBNE VRSTE TRIKOTNIKOV

Prav tako imamo posebne vrste trikotnikov s posebnimi lastnostmi, ki prinesejo nekaj zanimivih nalog in s tem načinov reševanja. Včasih zadostuje že en sam podatek. Več o vrstah trikotnikov si lahko ogledate na spletni strani HMTL: trikotnikVrste.html.

c1. Enakokraki trikotnik

c2. Enakostranični trikotnik

c3. Pravokotni trikotnik

b1. Višinska točka

Dani podatki:

c = 7 cm

α = 45°

v_c = 4 cm

0. Najprej narišemo skico trikotnika (ne pozabite vrisati v_c), znane količine obkrožimo.

1. Narišemo osnovnico c.

2. Najprej bomo narisali vzporednico, ki je od nosilke c oddaljena za razdaljo v_c, saj se nekje na njej nahaja točka C.

Na nosilki stranice c izberemo poljubno točko P in skoznjo narišemo pravokotnico.
Nato na pravokotnici odmerimo dolžino višine v_c (daljica v_c'). Dobimo točko R, skozi katero narišemo pravokotnico – s tem dobimo želeno vzporednico k nosilki c.

3. V točki A z geotrikotnikom odmerimo kot α in narišemo poltrak.

4. V presečišču vzporednice in kraka kota α dobimo oglišče C.

5. Dorišemo stranici trikotnika ∆ABC.

GeoGebra: trikotnikKonstrNal1vc.ggb

b2. Središče trikotniku očrtane krožnice

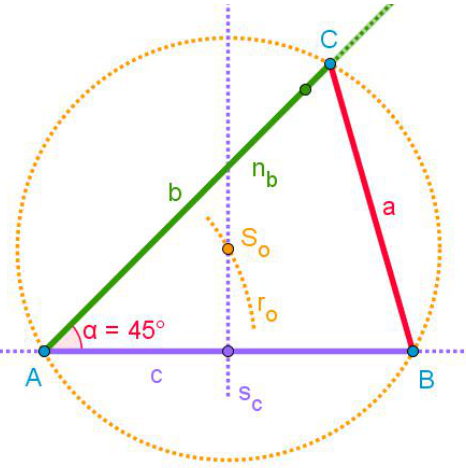
Dani podatki:

c = 7 cm

α = 45°

r_o = 4 cm

0. Najprej narišemo skico trikotnika (ne pozabite vrisati očrtanega kroga s polmerom r_o), znane količine obkrožimo.

1. Narišemo osnovnico c.

2. V točki A odmerimo kot α in narišemo nosilko n_b stranice b.

3. Narišemo simetralo s_c na osnovnico c (tj. pravokotnica na razpolovišče stranice c).

4. Iz točke A odmerimo lok r_o in v presečišču s simetralo s_c dobimo središče očrtane krožnice S_o.

5. Iz središča S_o očrtamo trikotniku očrtano krožnico s polmerom r_o.

6. V presečišču očrtane krožnice in nosilke stranice n_b dobimo oglišče C.

7. Dorišemo stranici trikotnika ∆ABC.

GeoGebra: trikotnikKonstrNal2ro.ggb

b3. Središče trikotniku včrtane krožnice

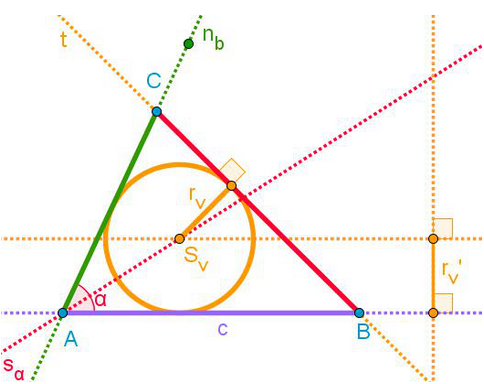
Dani podatki:

c = 8 cm

α = 65°

r_v = 2 cm

0. Najprej narišemo skico trikotnika (ne pozabite vrisati včrtanega kroga s polmerom r_v), znane količine obkrožimo.

1. Narišemo osnovnico c.

2. V točki A odmerimo kot α in narišemo nosilko n_bstranice b .

3. Narišemo simetralo s_α kota α, saj bo središče S_v včrtane krožnice ležalo nekje na tej simetrali.

4. Ker je polmer r_vvčrtane krožnice pravokoten na vse stranice ΔABC, narišemo vzporednico, ki je od nosilke c oddaljena za r_v.

5. V presečišču vporednice in simetrale s_α dobimo središče S_v včrtane krožnice.

6. Krožnico narišemo (polmer je seveda r_v).

6. Če narišemo tangento t na včrtano krožnico tako, da je pravokotna na polmer r_v in iti gre hkrati skozi točko B, dobimo v presečišču z nosilko n_boglišče C (pomagamo si z geotrikotnikom).

7. Dorišemo stranici trikotnika ∆ABC.

GeoGebra: trikotnikKonstrNal3rv.ggb

b4. Težišče trikotnika

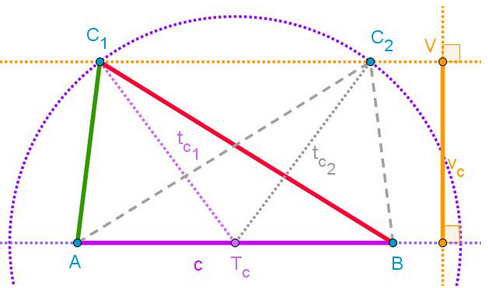
Dani podatki:

c = 7 cm

v_c = 4 cm

t_c = 5 cm

0. Najprej narišemo skico trikotnika (ne pozabite vrisati v_c in t_c), znane količine obkrožimo.

1. Narišemo osnovnico c.

2. Narisali bomo pas višine v_c. Na nosilki osnovnice c narišemo pravokotnico na to premico.

3. S šestilom odmerimo v_c in nanesemo razdaljo na pravokotnico (točka V).

4. Skozi dobljeno točko V narišemo vzporednico k nosilki daljice c.

5. Narisati moramo težiščnico t_c na osnovnico c, s čimer bomo dobili oglišče C. Najprej razpolovimo daljico c in dobimo točko T_c(najlaže s pomočjo simetrale stranice).

6. S šestilom odmerimo t_c in iz točke T_c in narišemo krožni lok.

7. V presečišču z vzporednico dobimo točko C. Ker sta dve taki možnosti, ima naloga dve rešitvi, C₁ in C₂, torej narišemo dva trikotnika.

GeoGebra: trikotnikKonstrNal4tc.ggb

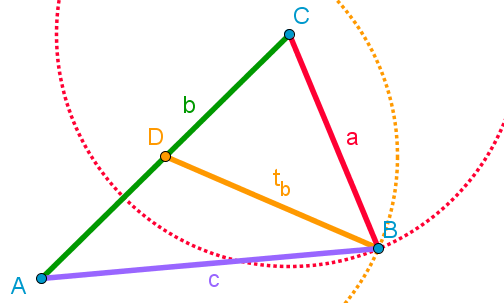
Dani podatki:

a = 4 cm

b = 6 cm

t_b = 4 cm

0. Najprej narišemo skico trikotnika (ne pozabite vrisati t_c), znane količine obkrožimo.

1. Narišemo stranico b.

2. Iz točke C narišemo krožni lok polmera stranice a (nekje na tem loku se bo nahajalo oglišče B).

3. Določimo razpolovišče D stranice b.

4. Iz točke D narišemo krožni lok polmera t_b.

5. V presečišču obeh lokov dobimo točko B.

6. Dorišemo stranici trikotnika ∆ABC.

GeoGebra: trikotnikKonstrNal4tcB.ggb

c1. Enakokraki trikotnik

Dani podatki:

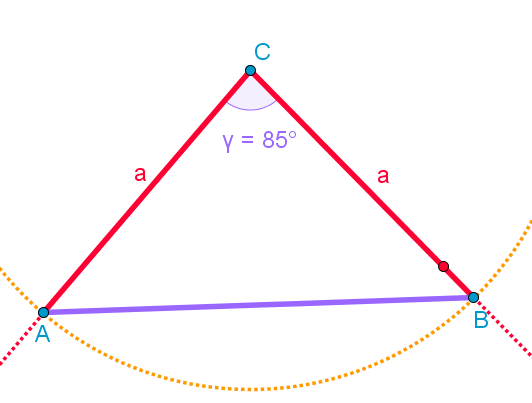
Enakokraki trikotnik

a = 5,5 cm

γ = 85°

0. Najprej narišemo skico trikotnika (ne pozabite dorisati, da sta kraka enaka, da sta kota ob osnovnici c enaka), znane količine obkrožimo.

1. Narišemo točko C in narišemo poljuben poltrak.

2. Glede na poltrak in točko C narišemo kot .

3. S šestilom odmerimo dolžino stranice a in narišemo krožni lok, ki seka narisana poltraka.

4. V presečišču poltrakov in krožnice dobimo točki A in B.

5. Dorišemo stranice trikotnika ∆ABC.

GeoGebra: trikotnikKonstrNal5enkrakA.ggb

Dani podatki:

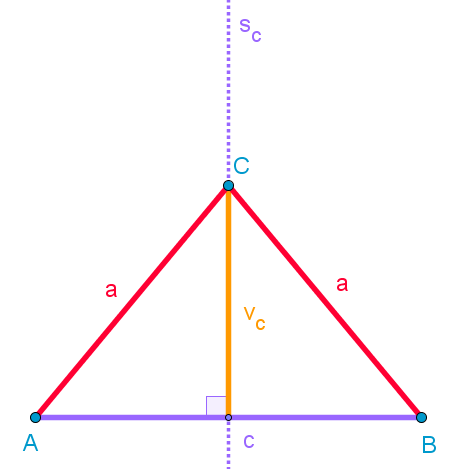
Enakokraki trikotnik

c = 5 cm

v_c= 3 cm

0. Najprej narišemo skico trikotnika (ne pozabite dorisati, da sta kraka enaka, da sta kota ob osnovnici c enaka), znane količine obkrožimo.

1. Narišemo stranico c.

2. Narišemo simetralo stranice sc.

3. Na simetrali sc odmerimo višino vc in dobimo oglišče C.

4. Dorišemo stranici trikotnika ∆ABC.

GeoGebra: trikotnikKonstrNal5enkrakB.ggb

c2. Enakostranični trikotnik

Dani podatki:

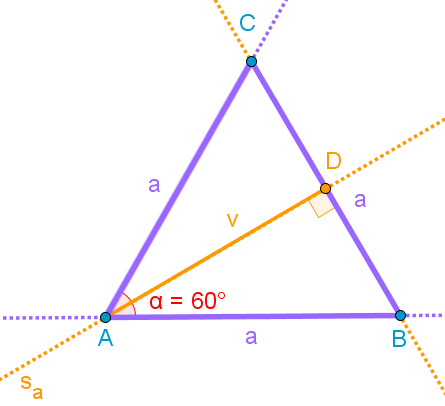
Enakostranični trikotnik

v = 4 cm

0. Najprej narišemo skico enakostraničnega trikotnika (ne pozabite vse stranice označiti z a in označiti kot 60°).

1. Narišemo nosilko bodoče stranice in nekje izberemo točko A.

2. V točki A narišemo kot 60°.

3. Narišemo simetralo kota s_a.

4. Na simetrali s_aodmerimo višino v in dobimo točko D.

5. V točki D narišemo pravokotnico na simetralo s_a.

Opomba: nalogo bi še laže rešili, če bi narisali pas, ki ga oriše višina v.

4. V presečišču simetrale s_ain krakov kota 60° dobimo točki B in C.

5. Dorišemo stranice trikotnika ∆ABC.

GeoGebra: trikotnikKonstrNal5enkstrA.ggb

Dani podatki:

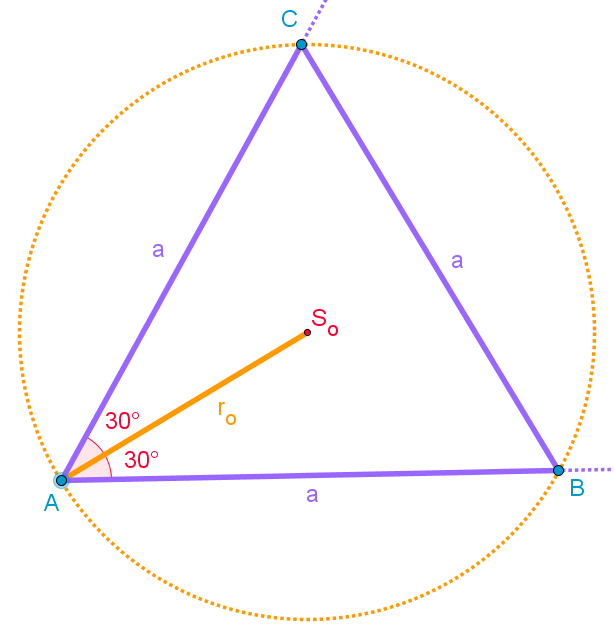
Enakostranični trikotnik

r_O = 4,5 cm (polmer očrtane krožnice)

0. Najprej narišemo skico enakostraničnega trikotnika (ne pozabite vse stranice označiti z a in označiti kot 60°, približno vrišemo tudi središče očrtane krožnice).

1. Narišemo krožnico s polmerom r_O in središčem S_O.

2. Na krožnici izberemo poljubno točko A in narišemo polmer r_O.

3. Glede na polmer r_Onarišemo kot 30° z vrhom v točki A (polovica kota 60°).

4. Narišemo še kot -30° z vrhom v točki A (druga polovica kota 60°).

5. Kjer se kraka kotov sekata s krožnico, dobimo točki B in C.

6. Dorišemo stranice trikotnika ∆ABC.

GeoGebra: trikotnikKonstrNal5enkstrB.ggb