ZNAMENITE TOČKE TRIKOTNIKA
Trikotnik
ima naslednje znamenite točke:
1.
Višinska točka:
Presečišče nosilk višin na stranice trikotnika.
2.
Središče trikotniku
očrtane krožnice: Presečišče simetral
stranic trikotnika.
3.
Središče trikotniku
včrtane krožnice: Presečišče simetral
kotov trikotnika.
4.
Težišče trikotnika:
Presečišče težiščnic na stranice
trikotnika.
5.
Eulerjeva premica:
Na tej premici ležijo višinska točka, središče trikotniku očrtane
krožnice ter težišče in središče
krožnice devetih točk (vse, razen
središče včratne krožnice).
Nekaj
tipov nalog, ki jih lahko rešimo s pomočjo znamenitih točk
trikotnika, si lahko ogledate na spletni strani HMTL:
trikotnikKonstrNal.html
Za
ogled datotek morate namestiti brezplačni program GeoGebra.
1.
Višinska točka
|
Višina je daljica, ki poteka
med ogliščem trikotnika in nosilko nasproti ležeče stranice in je
nanjo pravokotna (npr. med ogliščem C in pravokotnico na nosilko
stranice c je vc).
Trikotnik ima tri višine, va
, vb
in vc .
Nosilke višin trikotnika se
sekajo v eni točki, ki jo imenujemo višinska točka in jo označimo
z V.
GeoGebra:
trikotnikZnamTckVisinTck.ggb
|

|
2.
Središče trikotniku očrtane krožnice
|
Središče So
trikotniku očrtane krožnice dobimo v presečišču simetral stranic
trikotnika.
Krožnica gre skozi vsa tri
oglišča trikotnika. Polmer očrtane krožnice označimo z ro
in je hkrati razdalja med oglišči in središčem So.
GeoGebra:
simetralaDaljiceTOcrtanR.ggb
|

|
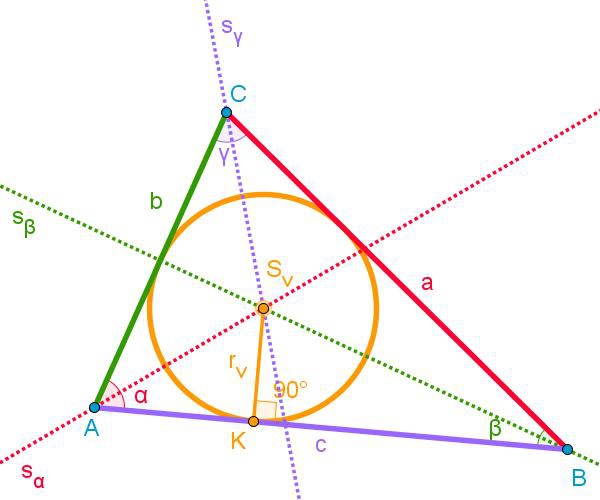
3.
Središče trikotniku včrtane krožnice
|
Središče Sv
trikotniku včrtane krožnice dobimo v presečišču simetral kotov
trikotnika.
Krožnica se v natančno eni
točki dotika vsake od stranic (tangenta), razdalja od središča Sv
do te točke pa je ravno polmer včrtane krožnice rv.
GeoGebra:
simetralaKotaTVcrtanR.ggb
|
|
4.
Težišče trikotnika
|
Težiščnica je daljica, ki
povezuje razpolovišče stranice trikotnika z nasproti ležečim
ogliščem.
Težiščnica tc
je tako daljica, ki povezuje razpolovišče daljice c z ogliščem C.
Podobno težišnici ta
in tb .
Opomba:
Tudi pri risanju središča očrtane krožnice poteka simetrala
stranice skozi razpolovišče te stranice.
GeoGebra:
trikotnikZnamTckTezisce.ggb
|

|
5.
Eulerjeva premica (dodatek)
Krožnica
devetih točk
|
Če v trikotniku ΔABC
označimo razpolovišča stranic z A1,
B1,
C1,
z V višinsko točko in s točkami A2,
B2
in C2
nožišča višin trikotnika, z A3,
B3
in C3
pa razpolovišča daljic med oglišči ΔABC
in višinsko točko V, potem vse točke ležijo na skupni krožnici.
To krožnico imenujemo krožica
devetih točk oziroma Feuerbachova krožnica.
GeoGebra:
trikotnikZnamTckKroznica9tck.ggb
|

|




