This
site is under construction.
Ioptlib
This page
provides some information about the Ioptlib (Investigative Optimization
Library), whose experimental version release is planned for
2008
(see comment on availability).
IOptLib is a free open source library.
|
|
About
the library
Ioptlib (a shortcut for Investigative Optimization Library) is
an open optimization library designed to sustain development and
testing of algorithms for solving practical optimization problems. A
priority goal is to develop algorithms suited to problems with
computationally expensive and possibly noisy evaluation of the response
(i.e. objective and constraint) functions. The library is intended to
provide modular building blocks for constructing such algorithms,
standardized templates for interfacing tools obtained form other
libraries, and testing environment where different performance aspects
of algorithms can be readily extensively tested during and after the
development stage. Currently most of the efforts are devoted to
algorithms based on successive solution of approximated problems
obtained by local sampling and approximation of the response functions.
Such algorithms have complex designs and involve solution of many
sub-problems such as non-linear or quadratic programming problems,
matrix algebra, optimal sampling strategies, etc. The intention is
therefore to gradually accumulate efficient routines for solving these
problems, which will lead to broader serviceability of the library. Any
attempt was made to keep open the possibility of starting development
of new algorithms or attaching to the existent functionality at any
level. The basic library is therefore intended to be distributed as
free open source under certain conditions. A couple of algorithms will
be available under different negotiable terms since this is necessary
to provide the funding for library development, however their building
blocks together with a set of quite useful algorithms will be provided
with the basic set that is more open what concerns availability.
The original motivation for the library was obtained in
optimization of forming processes where evaluation of objective and
constraint functions typically involves complex numerical simulation
with hundreds of thousands of degrees of freedom, very non-linear and
path dependent materials, multi-physics and multi-scale phenomena etc.
As result, not only the calculation of the objective and constraint
functions takes very long times even on the fastest computers or
parallel architectures, but these functions often contain substantial
amount of numerical noise. These conditions impose a substantial turn
in how algorithm performance is viewed. On one hand the most important
measure of algorithm efficiency becomes the number of function
evaluations it takes for calculating optimum up to a given accuracy.
The CPU time spent by the algorithm becomes somehow less important
because function evaluations will normally require incomparably more
computational time. Because running optimization procedures will often
be just on the limit of affordable, the goal will not always be to find
an optimal solution up to a specified accuracy, but rather to achieve
significant improvement within affordable computational time.
The targeted scope of the library is beyond the area of its
original motivation. It is intended to provide a pool of algorithms for
different problems and facilities for extending this pool. Beside that,
interaction with other libraries and use of the library in existing or
future software is accounted for as much as possible. A lot of stress
is put on defining standard data types and function prototypes used for
different purposes, such as evaluation of response functions and their
derivatives or for storing results of such evaluation and their use in
building approximations. These standards are defined in such a way that
routines for similar tasks from other libraries can be easily
incorporated in the system, and functions that are consistent with
library standards can be easily exported in standard forms required in
other software environments. Wrapping functions and data converters are
provided for some common cases, and the way how one can create own
tools for this is being documented in manuals. The standards are
designed in such a way that they are suitable for any environment, in
particular to allow recursive calls and work in multi-threaded
environment.
The library comes with a set of basic utilities that are
extensively used in implementation of basic building blocks and
algorithms. This includes e.g. basic matrix and vector operations and
generic implementation of data containers such as stacks. These
utilities are well documented in source code while overview is given in
documentation.
Many of elementary utilities make use of other free libraries.
Contribution of people who designed these libraries and made them
available is gratefully acknowledged.
Availability
The library will be available in 2008, however the exact
release date is not known yet. Until
then I would like to write some additional documentation and implement
some
routines which will make the library useful for other users. I intend
to release an experimental version first, which is mainly intended for
those who have an interest in contributing to the library or
cooperating at decisions about library design. After a given period,
the official version will be released. In the official versions, I will
attempt to enforce backward compatibility as much as possible for the
functionality that is intended for average users, while the
experimental version may be subject to changes in function names and
organization.
One of the users of the library will hopefully be C3M and the
library will be
at some stage included in the optimization software Inverse.
The library will be publically available without limitations
(including the source) under BSD license
in order to promote the exchange
of ideas between researchers working on similar problems in
optimization. Some commercial algorithms will not be freely available,
but I will do my best to make them easily available for research
purposes in exchange for quotation, exchange of results, or
contributions to the library.
Documentation
IOptLib
User's Manual. This manual
is mainly intended for users of the library, however the extent of
information is sufficient that it cna be advantageously used by
developers.
Simplex algorithms for nonlinear constraint
optimization problems. This documents containd description
of a set of modified Nelder-Mead simplex algorithms that can be used
for constraint nonlinear optimization. These algorithms can
beadvantageously used for optimization when gradients of the
objective and constraint functions are not available and where these
functions are not smooth. All the described algorithms are
implemented in IOptLib.
Igor's documentation.
Collection of useful documents by Igor Grešovnik.
Example: optimization by using
successive approximations of response
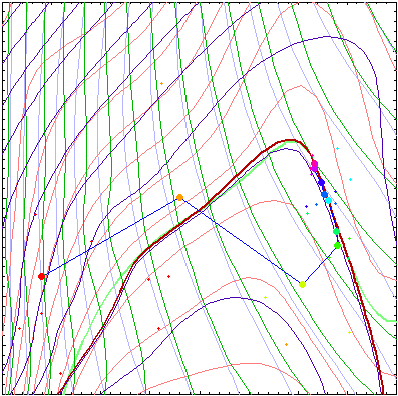
This figure represents convergence of an algorithm based
on successive approximation of the response functions. Contours of
actual objective and constraint function are shown in pale colors while
contours of approximated functions are plotted in stronger
colors. Zero constrsint contours (actual and approximated) are plotted
with thicker lines. Small points are the samplig points where the
response functions (loaded with some level of noise) were calculated,
and larger points are the solutions of the approximated problems.
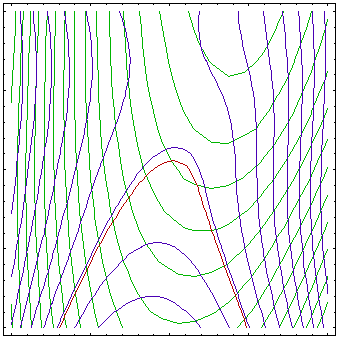
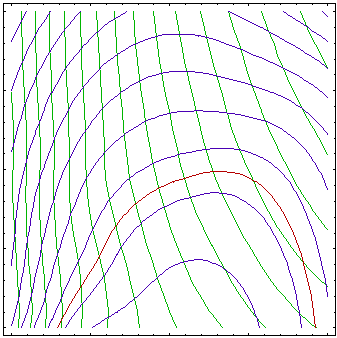
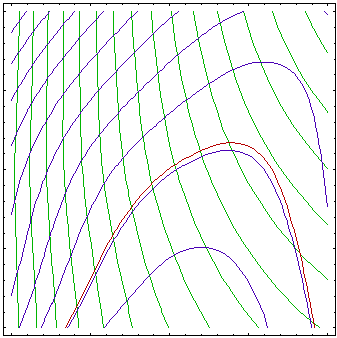
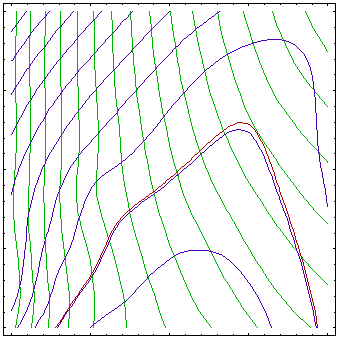
The figure above shows approximations of the objective (green
contours) and constraint functions (blue contours, brown 0 contour)
after 1, 3, 6 and 10 iterations of an algorithm based on successive
approximations. First, the approximations are very rough, with better
approximation around the initial point. Over iterations, center of the
approximated region moves towards optimum (see Figure above) and
approximation gets better around the optimum while region far from
optimum is not of interest and is not well approximated.
Updated in September 2007
|
Note: This site is under
construction.
Number of accesses: 
If you don't see the access counter properly then please follow this link!