Ducat nalog z grafi

1. Na sliki je graf linearne funkcije. Zapiši enačbo te funkcije.
   
   Rešitev:    \(f(x)=-\frac{1}{2}x+2\)
2. Na sliki je graf kvadratne funkcije. Zapiši enačbo te funkcije v splošni obliki.
   
   Rešitev:    \(f(x)=\frac{1}{4}x^2-x-3\)
3. Graf eksponentne funkcije \(f(x)=a^x\) poteka skozi točko \(A(2,3)\).
   

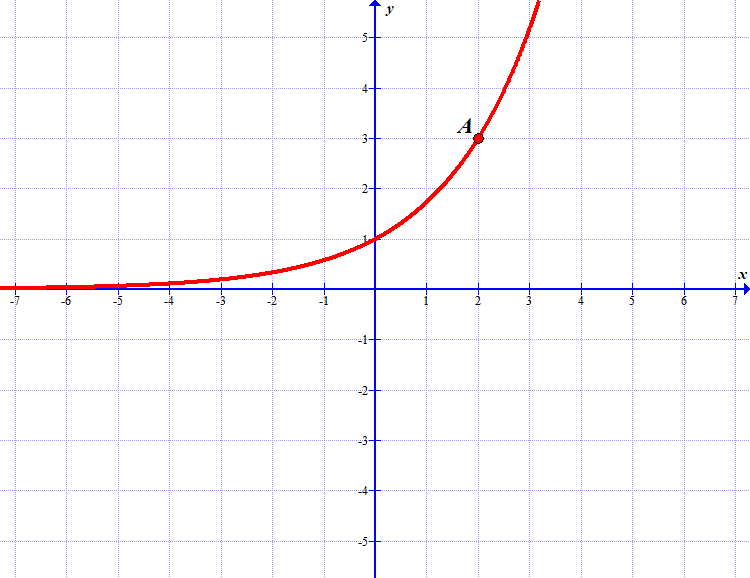
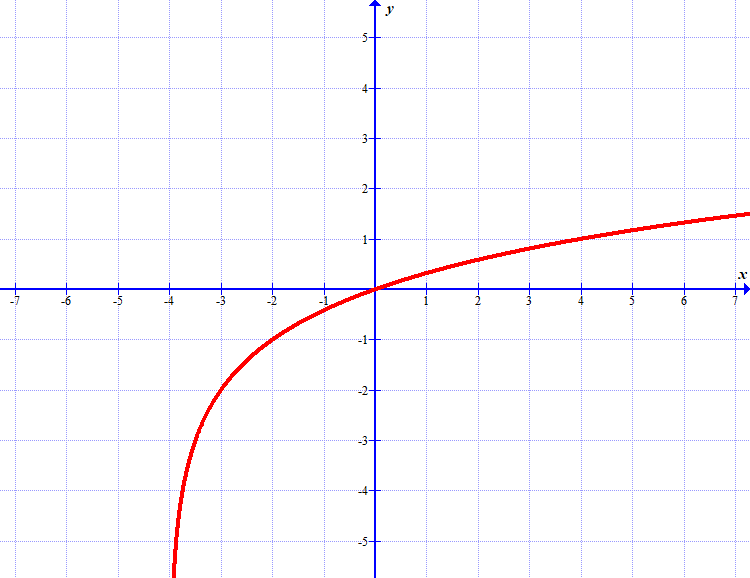
   (a)   Določi osnovo \(a\).

   (b)   Nariši graf funkcije \(g(x)=2-f(x)\) in zapiši zalogo vrednosti te funkcije.

   
   Rešitev:    (a)  \(a=\sqrt{3}\),     (b)  \(\mathcal{Z}_g=(-\infty,2)\)
4. Na sliki je graf funkcije z enačbo \(f(x)=\log_2(x+A)+B\). Določi realna parametra \(A\) in \(B\) ter zapiši enačbo te funkcije. Zapiši tudi definicijsko območje funkcije.
   
   Rešitev:    \(f(x)=\log_2 (x+4)-2\), definicijsko območje: \(\mathcal{D}_f=(-4,\infty)\)
5. Na sliki je graf funkcije, ki jo je možno zapisati v obliki \(f(x)=A\sin Bx+C\). Določi pozitivne parametre \(A,~B\) in \(C\) ter zapiši enačbo te funkcije.
   
   Rešitev:    \(f(x)=2\sin 3x+1\)
6. Na sliki je graf funkcije \(f(x)=\sin(ax+b)\). Določi vrednosti realnih parametrov \(a\) in \(b\). (Opomba: Možnih je več rešitev. Zapiši \(a\gt0\) in \(0\lt b\lt 2\pi\)).
   
   Rešitev:    \(a=2,~ b=\frac{5\pi}{3}\)
7. Polinom četrte stopnje ima realne koeficiente. Njegov graf prikazuje spodnja slika. Zapiši enačbo tega polinoma v ničelni in v splošni obliki.
   
   Rešitev:    Ničelna oblika: \(p(x)=\frac{1}{9}(x-1)^3(x+3)\), splošna oblika: \(p(x)=\frac{1}{9}x^4-\frac{2}{3}x^2+\frac{8}{9}x-\frac{1}{3}\)
8. Podan je polinom \(p(x)=\frac{3}{2}x^3-10x^2+ax+b\). Določi realna koeficienta \(a\) in \(b\), če poznaš graf tega polinoma:
   
   Rešitev:    \(a=\frac{39}{2}=19.5,~~ b=-9\)
9. Na sliki je graf funkcije z enačbo \({\displaystyle f(x)=\frac{Ax+B}{x+C}}\). Določi realne parametre \(A,~B\) in \(C\) ter zapiši enačbo te funkcije. Določi tudi enačbi obeh asimptot.
   
   Rešitev:    \(f(x)=\frac{2x-3}{x-1}\), asimptoti: \(x=1\) in \(y=2\)
10. Na spodnji sliki je graf racionalne funkcije, ki ima enačbo oblike \({\displaystyle f(x)=\frac{x^2+ax+b}{x^2+cx+d}}\). Izračunaj vrednosti neznanih koeficientov \(a,~ b,~ c\) in \(d\).
    
    Rešitev:    \(a=-2,~ b=0,~ c=0,~ d=-1\)
11. Na sliki je graf funkcije \(y=f(x)\).
    

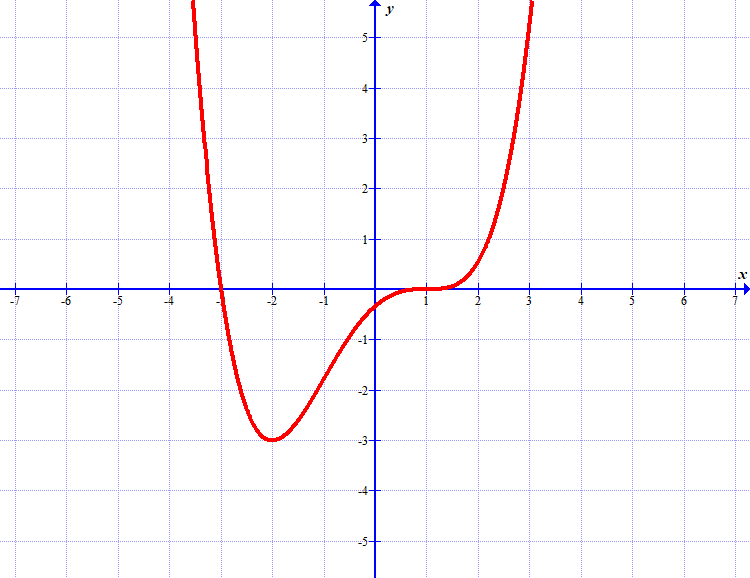
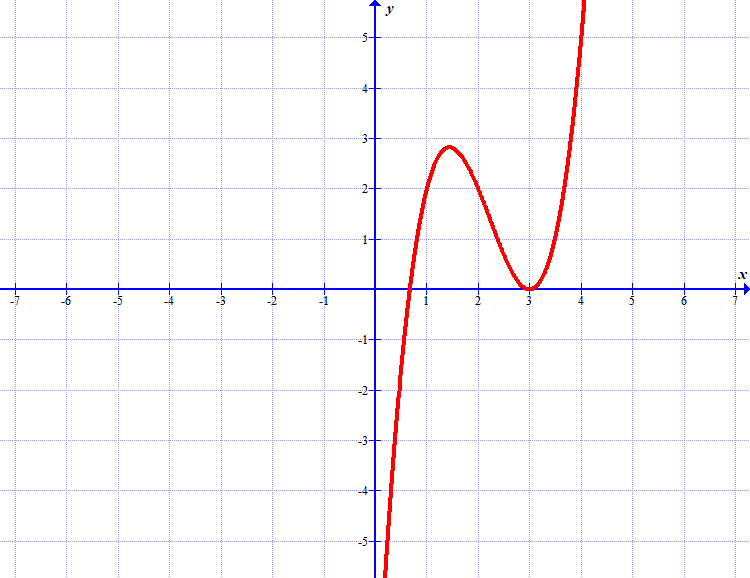
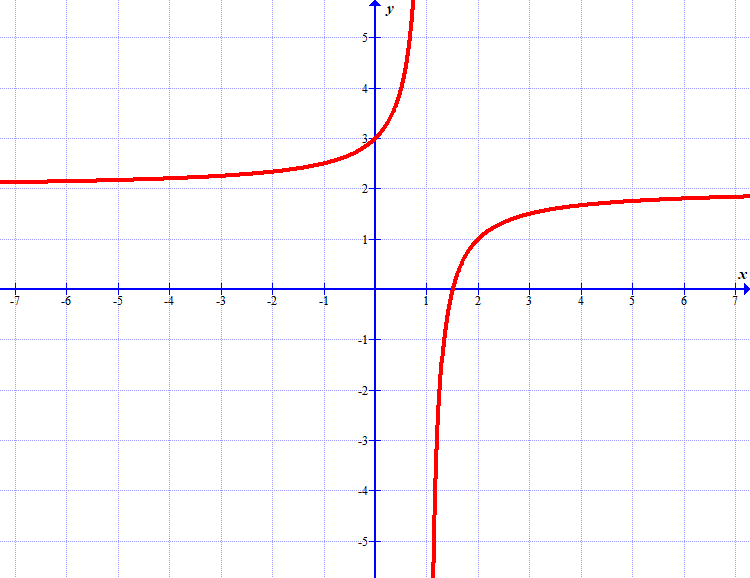
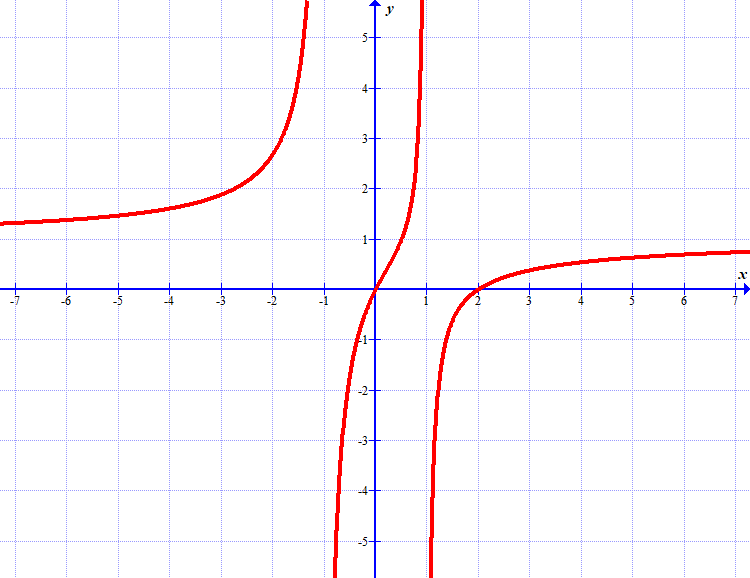
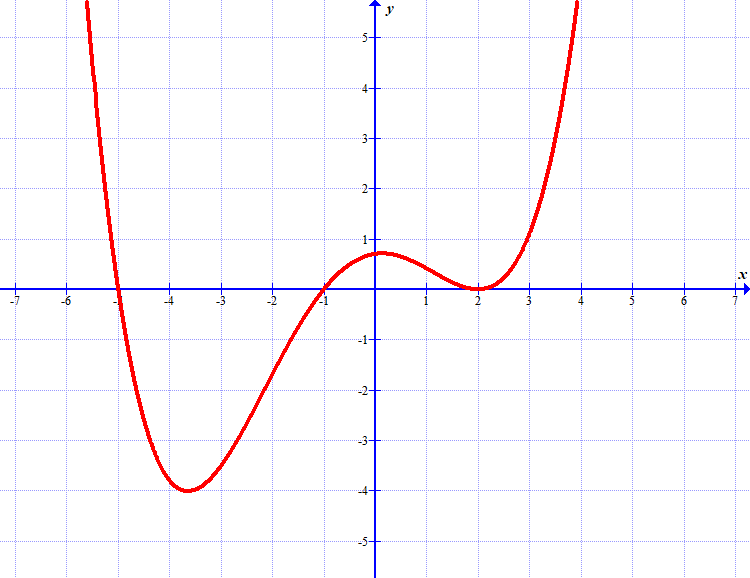
    (a)   Ugotovi, za katere \(x\) je odvod te funkcije negativen.

    (b)   Ugotovi, za katere \(x\) je odvod te funkcije pozitiven.

    
    Rešitev:    (a)  Odvod je negativen za \(x\in(-3,1)\),     (b)  odvod je pozitiven za \(x\in(-\infty,-3)\cup(1,\infty)\)
12. Dana je funkcija \(f\). Na spodnji sliki je graf odvoda te funkcije: \(y=f'(x)\).
    

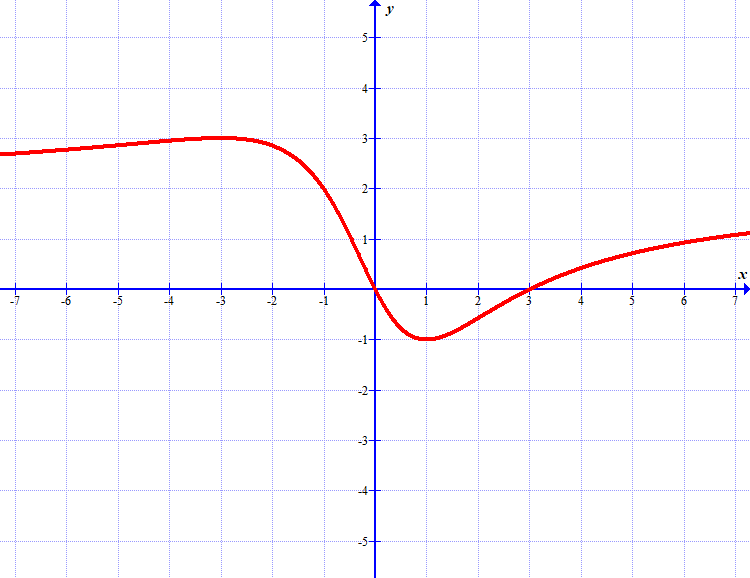
    (a)   Ugotovi, pri katerem \(x\) ima funkcija \(f\) maksimum.

    (b)   Ugotovi, pri katerem \(x\) ima funkcija \(f\) minimum.

    (c)   Ugotovi, pri katerem \(x\) ima funkcija \(f\) vodoravni prevoj.

    
    Rešitev:    (a)  Maksimum: \(x=-5\),     (b)  minimum: \(x=-1\),     (c)  vodoravni prevoj: \(x=2\)

 Domov