Trigonometrijske funkcije

Grafi trigonometrijskih funkcij

1. Nariši graf funkcije:
   

   (a)    \(y=3\sin x+2\)

   (b)    \(y=\sin(x-\frac{\pi}{3})\)

   (c)    \(y=2+\cos 3x\)

   (d)    \(y=1-2\sin\frac{x}{2}\)

   (e)    \(y=\cos(\frac{x}{2}-\frac{\pi}{4})\)

   (f)    \(y=\tan2x\)

2. Nariši graf funkcije:
   

   (a)    \(y=|2\sin2x|\)

   (b)    \(y=|\cot x|\)

   (c)    \(y=\sin(|x|+\frac{\pi}{6})\)

   (d)    \(y=\left|\sin(|x|+\frac{\pi}{6})\right|\)

   (e)    \(y=1-|\tan x|\)

3. Nariši graf funkcije:  \(y=\log_2(2\cos x)\)
   Namig:    Najprej nariši \(y_1=2 \cos x\) in nato logaritmiraj \(y\) koordinato vsake točke.
4. Nariši graf funkcije:  \(y=\cos x + \cos 2x\)
   Namig:    Najprej nariši \(y_1=\cos x\) in \(y_2=\cos 2x\), nato seštej \(y\) koordinati točk, ki pripadata dololčeni vrednosti \(x\).
5. Nariši graf in zapiši ničle, maksimume in minimume naslednje funkcije:
   

   (a)    \(f(x)=3\sin \frac{x}{2}\)

   (b)    \(f(x)=2\cos(2x-\frac{\pi}{3})\)

   Rešitev:    (a)  Ničle: \(x=2k\pi\),   max.: \(T(\pi+4k\pi,3)\),   min.: \(T(-\pi+4k\pi,-3)\);   \((k\in\mathbb{Z})\),     (b)  Ničle: \(x=\frac{5\pi}{12}+\frac{k\pi}{2}\),   max.: \(T(\frac{\pi}{6}+k\pi,2)\),   min.: \(T(\frac{2\pi}{3}+k\pi,-2)\);   \((k\in\mathbb{Z})\)
6. Zapiši definicijsko območje in zalogo vrednosti za funkcijo:
   

   (a)    \(f(x)=3-2\cos4x\)

   (b)    \(f(x)=\tan(\frac{\pi}{4}-x)\)

   (c)    \(f(x)=\left| \tan \frac{x}{2} \right|\)

   Rešitev:    (a)  \(\mathcal{D}_f=\mathbb{R},~ \mathcal{Z}_f=[1,5]\),     (b)  \(\mathcal{D}_f=\mathbb{R}\setminus\{-\frac{\pi}{4}+k\pi;~k\in\mathbb{Z}\},~ \mathcal{Z}_f=\mathbb{R}\),     (c)  \(\mathcal{D}_f=\mathbb{R}\setminus\{\pi+2k\pi;~k\in\mathbb{Z}\},~ \mathcal{Z}_f=\mathbb{R}_0^{+}\)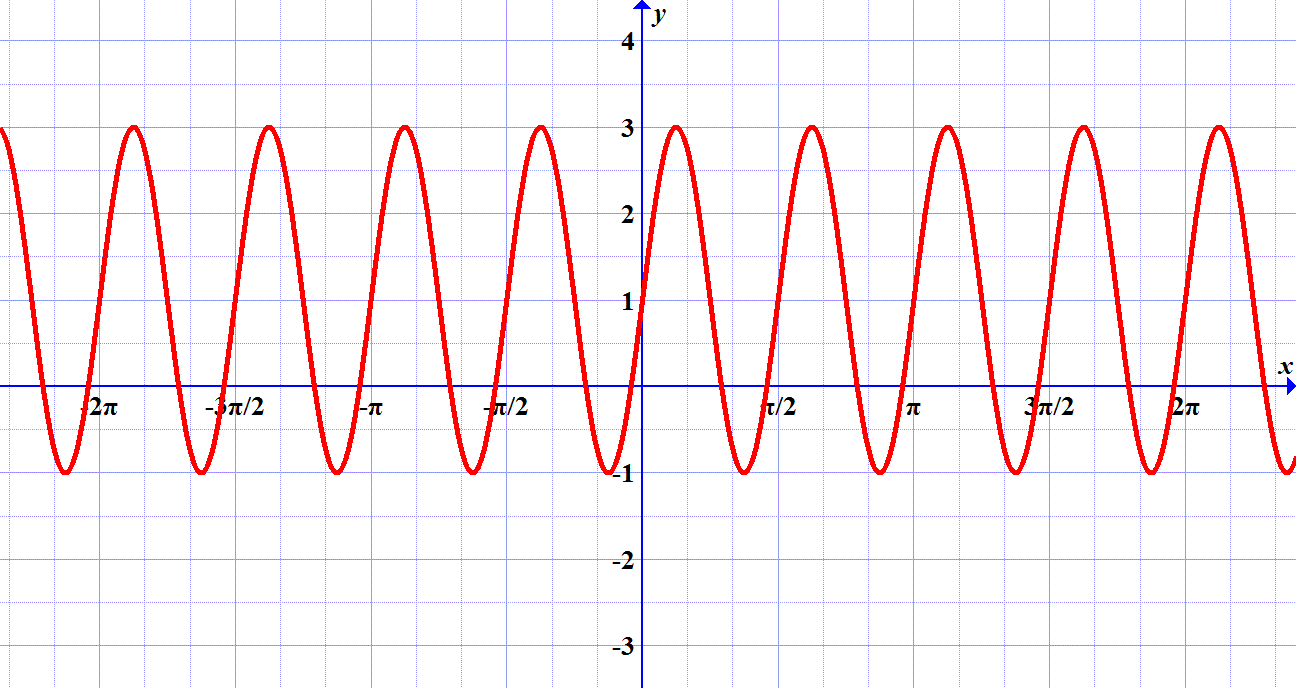
7. Na spodnji sliki je narisan graf funkcije \(f\). Zapiši enačbo te funkcije v obliki \(f(x)=A \sin Bx +C\).
   

   

   Rešitev:    \(f(x)=2 \sin 4x +1\).

Trigonometrijske enačbe

8. Reši enačbo:
   

   (a)    \(\sin2x=\frac{1}{2}\)

   (b)    \(\tan(x+\frac{\pi}{6})=\sqrt{3}\)

   (c)    \(1+\sqrt{2}\cos(x+\frac{\pi}{4})=0\)

   Rešitev:    (a)  \(x_1=\frac{\pi}{12}+k\pi,~ x_2=\frac{5\pi}{12}+k\pi;~ k\in\mathbb{Z}\),     (b)  \(x=\frac{\pi}{6}+k\pi;~ k\in\mathbb{Z}\),     (c)  \(x_1=\frac{\pi}{2}+2k\pi,~ x_2=-\pi+2k\pi;~ k\in\mathbb{Z}\)
9. Reši enačbo:
   

   (a)    \(2\cos^2 x-9\cos x+4=0\)

   (b)    \(\sin^2 x=\sin x+2\)

   (c)    \(2\sin^2 x-5=7\cos x\)

   Rešitev:    (a)  \(x=\pm\frac{\pi}{3}+2k\pi;~ k\in\mathbb{Z}\),     (b)  \(x=-\frac{\pi}{2}+2k\pi;~ k\in\mathbb{Z}\),     (c)  \(x=\pm\frac{2\pi}{3}+2k\pi;~ k\in\mathbb{Z}\)
10. Reši enačbo:
    

    (a)    \(\cos^2 x+\cos x=0\)

    (b)    \(\sin2x-\sin x=0\)

    (c)    \(\sin^3 x-4\sin^2 x+3\sin x=0\)

    Rešitev:    (a)  \(x_1=\frac{\pi}{2}+k\pi,~ x_2=\pi+2k\pi;~ k\in\mathbb{Z}\),     (b)  \(x_1=k\pi,~ x_2=\pm\frac{\pi}{3}+2k\pi;~ k\in\mathbb{Z}\),     (c)  \(x_1=k\pi,~ x_2=\frac{\pi}{2}+2k\pi;~ k\in\mathbb{Z}\)
11. Reši enačbo:
    

    (a)    \(\sin x+\sqrt{3}\cos x=0\)

    (b)    \(\sin^2 x-6\sin x\cos x+5\cos^2 x=0\)

    (c)    \(2\sin^2 x-\sin2x-2\cos^2 x=1\)

    Rešitev:    (a)  \(x=-\frac{\pi}{3}+k\pi;~ k\in\mathbb{Z}\),     (b)  \(x_1=\frac{\pi}{4}+k\pi,~ x_2=\arctan 5+k\pi;~ k\in\mathbb{Z}\),     (c)  \(x_1=-\frac{\pi}{4}+k\pi,~ x_2=\arctan 3+k\pi;~ k\in\mathbb{Z}\)
12. Reši enačbo:
    

    (a)    \(\sin5x-\sin x=0\)

    (b)    \(\cos3x=\cos(x+\frac{\pi}{3})\)

    (c)    \(\sin x=\cos(x-\frac{\pi}{4})\)

    Rešitev:    (a)  \(x_1=\frac{k\pi}{2},~ x_2=\frac{\pi}{6}+\frac{k\pi}{3};~ k\in\mathbb{Z}\),     (b)  \(x_1=-\frac{\pi}{12}+\frac{k\pi}{2},~ x_2=\frac{\pi}{6}+k\pi;~ k\in\mathbb{Z}\),     (c)  \(x=\frac{3\pi}{8}-k\pi;~ k\in\mathbb{Z}\)
13. Reši enačbo:
    

    (a)    \(\sin2x=2\cos^2 x\)

    (b)    \({\displaystyle\Big(\cos x+\frac{1}{\cos x}\Big)^{-1}=\frac{2}{5}}\)

    (c)    \({\displaystyle 5\cot x-2\sin x = \frac{1}{\sin x}}\)

    (d)    \({\displaystyle \tan x+\frac{\tan x}{\cos x}=2\tan x \cos x}\)

    (e)    \(\sin 5x \cos 3x=\sin 4x \cos 2x\)

    (f)    \({\displaystyle \cot x+\frac{1}{\sin x}=0}\)

    Rešitev:    (a)  \(x_1=\frac{\pi}{2}+k\pi,~ x_2=\frac{\pi}{4}+k\pi;~ k\in\mathbb{Z}\),     (b)  \(x=\pm\frac{\pi}{3}+2k\pi;~ k\in\mathbb{Z}\),     (c)  \(x=\pm\frac{\pi}{3}+2k\pi;~ k\in\mathbb{Z}\),     (d)  \(x_1=k\pi,~ x_2=\pm\frac{2\pi}{3}+2k\pi;~ k\in\mathbb{Z}\),     (e)  \(x_1=k\pi,~ x_2=\frac{\pi}{14}+\frac{k\pi}{7};~ k\in\mathbb{Z}\),     (f)  Enačba nima rešitve (\(x=\pi+2k\pi\) odpade pri preizkusu).

Kot med premicama

14. Izračunaj naklonski kot premice (rezultat zapiši v stopinjah in minutah):
    

    (a)    \(y=5x+1\)

    (b)    \(5x+3y=7\)

    (c)    \(x-5=0\)

    Rešitev:    (a)  \(\alpha\doteq78^\circ41'\),     (b)  \(\alpha\doteq-59^\circ2'\) ali tudi \(\alpha\doteq120^\circ58'\),     (c)  \(\alpha=90^\circ\)
15. Premica \(p\) ima enačbo: \(\frac{\textstyle x}{\textstyle 8}-\frac{\textstyle y}{\textstyle 6}=1\). Izračunaj kot \(\alpha\), ki ga premica oklepa z vodoravno osjo, in kot \(\beta\), ki ga ta premica oklepa z navpično osjo. Kota zapiši v stopinjah in minutah.
    Rešitev:    \(\alpha\doteq36^\circ52',~ \beta\doteq53^\circ8'\)
16. Izračunaj ostri kot med premicama \(p\) in \(q\) (rezultat zapiši v stopinjah in minutah):
    

    (a)    \(p\!:~ y=4x+1\),    \(q\!:~ y=\frac{\textstyle 1}{\textstyle 3}x-2\)

    (b)    \(p\!:~ 4x-6y=3\),    \(q\!:~ 9x+6y=4\)

    (c)    \(p\!:~ 5x-2y=0\),    \(q\!:~ 5x-10=0\)

    Rešitev:    (a)  \(\varphi\doteq57^\circ32'\),     (b)  \(\varphi=90^\circ\),     (c)  \(\varphi\doteq21^\circ48'\)
17. Dani sta točki \(A(-2,5)\) in \(B(6,7)\). Premica \(p\) poteka skozi točki \(A\) in \(B\), premica \(q\) pa poteka skozi točko \(A\) in skozi izhodišče koordinatnega sistema. Izračunaj, koliko meri ostri kot, ki ga oklepata premici \(p\) in \(q\). Kot zapiši v stopinjah in minutah.
    Rešitev:    \(\varphi\doteq82^\circ14'\)
18. Dana je premica \(p\!:~ 2x-4y+1=0\). Zapiši enačbo premice \(q\), ki oklepa kot \(90^\circ\) s premico \(p\) in poteka skozi točko \(T(5,-7)\).
    Rešitev:    \(q\!:~ y=-2x+3\)
19. Dana je premica \(p\!:~ y=\frac{\textstyle 3}{\textstyle 5}x+2\). Premica \(q\) oklepa kot \(45^\circ\) s premico \(p\) in poteka skozi točko \(T(0,2)\). Zapiši enačbo premice \(q\) (navedi vse možne rešitve).
    Rešitev:    Dve rešitvi: \(q_1\!:~ y=4x+2,~~ q_2\!:~ y=-\frac{1}{4}x+2\)
20. Premica \(p\) ima enačbo: \(\frac{\textstyle x}{\textstyle 3}-\frac{\textstyle y}{\textstyle \sqrt{3}}=1\). Zapiši enačbi premic \(q_1\) in \(q_2\), ki potekata skozi koordinatno izhodišče in oklepata s premico \(p\) kot \(30^\circ\).
    Rešitev:    \(q_1\!:~ y=\sqrt{3}x,~~ q_2\!:~ y=0\)

 Domov