-
Izračunaj teme in ničli ter nariši graf kvadratne funkcije:
(a) \(f(x)=x^2-2x-3\)
(b) \(f(x)=-x^2+3x+4\)
(c) \(f(x)=2x^2-4\)
(d) \(f(x)=\frac{1}{2}x^2-2x+2\)
Rešitev:
(a) \(T(1,-4),~ x_1=-1,~ x_2=3\),
(b) \(T(\frac{3}{2},\frac{25}{4}),~ x_1=-1,~ x_2=4\),
(c) \(T(0,-4),~ x_1=-\sqrt{2},~ x_2=\sqrt{2}\),
(d) \(T(2,0),~ x_{1,2}=2\)
Grafe funkcij lahko preveriš s programom Graph.
-
Izračunaj teme in ničli ter nariši graf kvadratne funkcije:
(a) \(f(x)=(2+x)(2-x)\)
(b) \(f(x)=2x(x+3)\)
(c) \(f(x)=\frac{1}{2}x(x-4)+4\)
Rešitev:
(a) \(T(0,4),~ x_1=-2,~ x_2=2\),
(b) \(T(-\frac{3}{2},-\frac{9}{2}),~ x_1=0,~ x_2=-3\),
(c) \(T(2,2)\), funkcija nima realnih ničel (v kompleksnem pa ima ničli: \(x_1=2-2i,~ x_2=2+2i\))
-
Dana je kvadratna funkcija \(f(x)=(2x-4)(x-4)-6\). Zapiši enačbo te funkcije v vseh treh značilnih oblikah in nariši graf.
Rešitev:
Splošna oblika: \(f(x)=2x^2-12x+10\), temenska oblika: \(f(x)=2(x-3)^2-8\), ničelna oblika: \(f(x)=2(x-1)(x-5)\).
-
Izračunaj vse (tudi nerealne) ničle danih funkcij. Rezultati naj bodo točni.
(a) \(f(x)=\frac{1}{2}x^2-3x+2\)
(b) \(f(x)=x^2\sqrt{2}-2x\sqrt{3}\)
(c) \(f(x)=2x^2-3x+\frac{13}{8}\)
Rešitev:
(a) \(x_1=3-\sqrt{5},~ x_2=3+\sqrt{5}\),
(b) \(x_1=0,~ x_2=\sqrt{6}\),
(c) \(x_1=\frac{3}{4}-\frac{1}{2}i,~ x_2=\frac{3}{4}+\frac{1}{2}i\)
-
Graf kvadratne funkcije poteka skozi točke \(A(1,-2),~ B(2,-1)\) in \(C(3,4)\).
Zapiši enačbo te kvadratne funkcije v splošni obliki.
Rešitev:
\(f(x)=2x^2-5x+1\)
-
Kvadratna funkcija ima teme v točki \(T(4,6)\). Graf te funkcije seka simetralo lihih kvadrantov v dveh točkah:
ena od njiju je točka \(A(2,2)\). Zapiši enačbo te kvadratne funkcije v splošni obliki in nariši graf.
Rešitev:
\(f(x)=-x^2+8x-10\)
-
Graf kvadratne funkcije seka abscisno os pri \(x_1=2\) in \(x_2=4\), ordinatno os pa pri \(y=-4\).
Zapiši enačbo te kvadratne funkcije v splošni obliki in nariši graf.
Rešitev:
\(f(x)=-\frac{1}{2}x^2+3x-4\)
-
Kvadratna funkcija ima ničli \(x_1=2-\sqrt{2}\) in \(x_2=2+\sqrt{2}\). Graf te funkcije poteka skozi točko \(A(3,-2)\)
Zapiši enačbo te kvadratne funkcije v temenski obliki in nariši graf.
Rešitev:
\(f(x)=2(x-2)^2-4\)
-
Kvadratna funkcija ima teme \(T(3,-1)\) in ničli \(x_1=3-i\) in \(x_2=3+i\).
Zapiši enačbo te kvadratne funkcije v splošni obliki in nariši graf.
Rešitev:
\(f(x)=-x^2+6x-10\)
-
Zapiši v splošni obliki enačbo kvadratne funkcije, katere graf je na spodnji sliki.
Rešitev:
\(f(x)=\frac{1}{4}x^2-\frac{1}{2}x-2\)
-
Kvadratna funkcija ima enačbo \(f(x)=2x^2+mx-3\).
Določi realni parameter \(m\) tako,
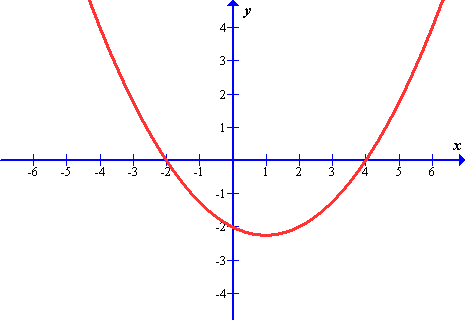
(a) da bo graf potekal skozi točko \(A(3,6)\),
(b) da bo \(x=-3\) ničla te funkcije.
Rešitev:
(a) \(m=-3\),
(b) \(m=5\)
-
Dana je kvadratna funkcija \(f(x)=x^2-mx+m+3\).
Določi \(m\in\mathrm{I\!R}\) tako, da bo teme te funkcije ležalo:
(a) na ordinatni osi,
(b) na abscisni osi.
Rešitev:
(a)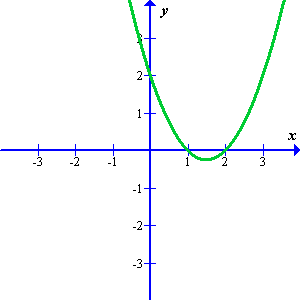 \(m=0\),
(b) \(m_1=-2,~ m_2=6\)
-
Dana je družina kvadratnih funkcij \(f(x)=\frac{1}{4}x^2-mx+m^2+m-2\).
Ugotovi, katera funkcija iz te družine ima teme na premici z enačbo \(y=2x-11\).
Zapiši parameter \(m\) in enačbo ustrezne funkcije.
Rešitev:
\(m=3,~~ f(x)=\frac{1}{4}x^2-3x+10\)
-
V koordinatnem sistemu (desno) je narisan graf funkcije \(f(x)=x^2-3x+2\).
Če ta graf prezrcalimo čez koordinatno izhodišče, dobimo graf funkcije \(g\).
Nariši graf funkcije \(g\) v isti koordinatni sistem in zapiši enačbo funkcije \(g\) v splošni obliki.
Rešitev:
\(g(x)=-x^2-3x-2\)
-
Reši naslednje enačbe (v \(\mathbb{C}\)). Zapiši točne vrednosti rešitev.
(a) \(2x^2-10x-28=0\)
(b) \(4x^2-9x+2=0\)
(c) \(9x^2+12x+4=0\)
(d) \(x^2-6x+13=0\)
Rešitev:
(a) \(x_1=-2,~ x_2=7\),
(b) \(x_1=\frac{1}{4},~ x_2=2\),
(c) \(x=-\frac{2}{3}\),
(d) \(x_1=3-2i,~ x_2=3+2i\)
-
Reši enačbe:
(a) \(2x(x-2)^2 = x^2 + 4x\)
(b) \((x+4)^3 - x(x-1)(x+1) = 35(x+2)\)
(c) \((x+1)^3=x^3+10x-1\)
(d) \((x-1)^3+(x-2)^3=11x-9\)
Rešitev:
(a) \(x_1=\frac{1}{2},~ x_2=4,~ x_3=0\),
(b) \(x_1=-\frac{3}{2},~ x_2=\frac{1}{3}\),
(c) \(x_1=2,~ x_2=\frac{1}{3}\),
(d) \(x_1=4,~ x_2=\frac{1}{2},~ x_3=0\)
-
Reši enačbe:
(a) \(x^4-19x^2+48=0\)
(b) \((x^2-7x+10)^2-2(x^2-7x+10)-8=0\)
(c) \({\displaystyle 2\cdot\Big(\frac{2}{x-3}\Big)^2-3\cdot\Big(\frac{2}{x-3}\Big)+1=0}\)
Namig:
Pomagaj si z uvedbo nove neznanke.
Rešitev:
(a) \(x_1=4,~ x_2=-4,~ x_3=\sqrt{3},~ x_4=-\sqrt{3}\),
(b) \(x_1=1,~ x_2=3,~ x_3=4,~ x_4=6\),
(c) \(x_1=5,~ x_2=7\)
-
Reši enačbe:
(a) \(1+\sqrt{4x+8}=x\)
(b) \({\displaystyle \frac{1+\sqrt{x+21}}{x-2}-3=0}\)
(c) \({\displaystyle \frac{3-\sqrt{x+4}}{x-5}=-2}\)
Rešitev:
(a) \(x=7\),
(b) \(x=4\),
(c) enačba ni rešljiva.
-
Reši enačbo \(\sqrt{2x+15}+\sqrt{x+7}=5\)
Rešitev:
\(x=-3\)
-
Produkt dveh števil je enak 448. Izračunaj ti dve števili, če veš, da je prvo število za 2 večje od polovice drugega.
Rešitev:
To sta števili 16 in 28 ali pa števili –14 in –32.
-
Pravokotnik ima obseg \(94~\mathrm{cm}\), diagonala tega pravokotnika pa meri \(37~\mathrm{cm}\). Izračunaj, koliko
merita stranici pravokotnika.
Rešitev:
Stranici merita \(12~\mathrm{cm}\) in \(35~\mathrm{cm}\) (ali \(a=12~\mathrm{cm},~ b=35~\mathrm{cm}\) ali pa
\(a=35~\mathrm{cm},~ b=12~\mathrm{cm}\)).
-
V pravokotnem trikotniku je kateta \(b\) za \(1~\mathrm{cm}\) daljša od katete \(a\), hipotenuza \(c\) pa je za
\(8~\mathrm{cm}\) daljša od katete \(b\). Izračunaj, koliko merijo stranice tega trikotnika.
Rešitev:
Stranice merijo: \(a=20~\mathrm{cm},~ b=21~\mathrm{cm},~ c=29~\mathrm{cm}\).
-
Dan je vektor \(\stackrel{\rightharpoonup}{a}=(m,m+3,3m)\). Določi pozitivno število \(m\) tako, da bo veljalo
\(|\stackrel{\rightharpoonup}{a}|=21\).
Rešitev:
\(m=6\)
-
Kvader z višino \(17~\mathrm{cm}\) ima za osnovno ploskev kvadrat. Površina tega kvadra meri \(1222~\mathrm{cm}^2\).
Izračunaj prostornino tega kvadra.
Rešitev:
\(V=2873~\mathrm{cm}^3\)
-
Če število \(m\in\mathrm{I\!R}^{+}\) korenimo in dobljeni rezultat prištejemo številu \(m\), dobimo 3540. Izračunaj \(m\).
Rešitev:
\(m=3481\)
-
Dana je enačba \(2x^2-5x+2m-7=0\). Določi \(m\in\mathrm{I\!R}\) tako, da bo ena od rešitev te enačbe \(x_1=1\). Izračunaj, koliko je
v tem primeru druga rešitev.
Rešitev:
\(m=5,~ x_2=\frac{3}{2}\)
-
Dana je enačba \(4x^2-20x+8m=7\). Določi \(m\in\mathrm{I\!R}\) tako, da bo imela ta enačba točno eno rešitev.
To rešitev tudi izračunaj.
Rešitev:
\(m=4,~ x=\frac{5}{2}\)
-
Dana je enačba \(mx^2+(2m+4)x+m+5=0\). Določi \(m\in\mathrm{I\!R}\) tako, da bo imela ta enačba točno eno rešitev.
To rešitev tudi izračunaj.
Rešitev:
Lahko je \(m=4,~ x=-\frac{3}{2}\), lahko pa tudi \(m=0,~ x=-\frac{5}{4}\).
-
Dana je kvadratna funkcija \(f(x)=x^2-x-3\). Izračunaj, v katerih točkah graf te funkcije seka premico z enačbo:
(a) \(y=3x+2\)
(b) \(y=3x-7\)
(c) \(y=3x-11\)
Rešitev:
(a) \(P_1(5,17),~ P_2(-1,-1)\),
(b) \(P(2,-1)\),
(c) graf ne seka premice.
-
Izračunaj, v katerih točkah se sekata grafa funkcij \(f(x)=x^2+3x-4\) in \(g(x)=-x^2+2x+2\).
Rešitev:
\(P_1(-2,-6),~ P_2(\frac{3}{2},\frac{11}{4})\)
-
Izračunaj presečišče grafov funkcij \(f(x)=\sqrt{3x+1}\) in \(g(x)=x-3\).
Rešitev:
\(P(8,5)\)
-
Izračunaj, v kateri točki graf funkcije \(f(x)=\sqrt{x-2}\) seka premico
\({\displaystyle \frac{x}{3}-\frac{y}{2}=1}\).
Rešitev:
\(P(6,2)\)
-
Dana je funkcija \(f(x)=2-\sqrt{9-8x}\). Izračunaj, v katerih točkah graf funkcije seka simetralo lihih kvadrantov.
Rešitev:
\(P_1(1,1),~ P_2(-5,-5)\)
-
Dani sta funkciji \(f(x)=x^2-4x+m+1\) in \(g(x)=2x-4\). Določi realni parameter \(m\) tako, da bosta imela grafa teh dveh
funkcij točno eno presečišče. Zapiši tudi koordinati tega presečišča.
Rešitev:
\(m=4,~ P(3,2)\)
-
Dana je enačba \(8x^2-12x+1=0\). Izračunaj vrednost izraza \(x_1^2+x_2^2\), če sta \(x_1\) in \(x_2\) rešitvi te enačbe.
Namig:
Uporabiš lahko Viètovi pravili za vsoto in produkt rešitev enačbe.
Rešitev:
\(x_1^2+x_2^2=2\)
-
Kvadratna funkcija \(f(x)=x^2-4x+20\) ima v \(\mathbb{C}\) dve ničli: \(x_1\) in \(x_2\).
Izračunaj vrednost izraza \((x_1^{-1}+x_2^{-1})^{-1}\).
Namig:
Uporabiš lahko Viètovi pravili za vsoto in produkt ničel funkcije.
Rešitev:
\((x_1^{-1}+x_2^{-1})^{-1}=5\)
-
Reši neenačbe:
(a) \(x^2-7x+10 \leqslant 0\)
(b) \(2x^2 \gt 6x\)
(c) \(2x-\frac{1}{3} \geqslant 3x^2\)
(d) \((2x+3)x \lt -4\)
Rešitev:
(a) \(x\in[2,5]\),
(b) \(x\in(-\infty,0)\cup(3,\infty)\),
(c) \(x=\frac{1}{3}\),
(d) neenačba nima rešitve.
-
Dana je neenačba: \(x^2-6x+m\leqslant 0\).
Določi realni parameter \(m\) tako,
(a) da bo imela neenačba eno samo rešitev,
(b) da bo množica rešitev te neenačbe interval širine 4.
Rešitev:
(a) \(m=9\),
(b) \(m=5\)
