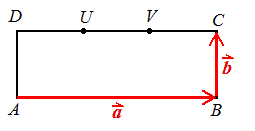Vektorji v ravnini

Linearne kombinacije vektorjev

1. V pravokotniku \(ABCD\) točki \(U\) in \(V\) delita stranico \(DC\) na tri skladne dele.\(\newcommand{\vekt}[1]{{\stackrel{\rightharpoonup}{{#1\,}}}}\) V tem pravokotniku sta podana vektorja \(\vekt{a}=\vekt{AB}\) in \(\vekt{b}=\vekt{BC}\). Izrazi naslednje vektorje kot linearne kombinacije vektorjev \(\vekt{a}\) in \(\vekt{b}\):
   

   (a)    \(\vekt{AC}\)

   (b)    \(\vekt{AU}\)

   (c)    \(\vekt{VU}\)

   (d)    \(\vekt{VA}\)

   Rešitev:    (a)  \(\vekt{AC}=\vekt{a}+\vekt{b}\),     (b)  \(\vekt{AU}=\frac{1}{3}\!\vekt{a}+\vekt{b}\),     (c)  \(\vekt{VU}=-\frac{1}{3}\!\vekt{a}\),     (d)  \(\vekt{VA}=-\frac{2}{3}\!\vekt{a}-\vekt{b}\)
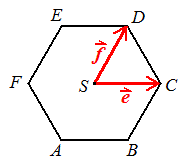2. Podan je pravilni šestkotnik \(ABCDEF\). Središče tega šestkotnika je točka \(S\). V tem šestkotniku sta podana vektorja \(\vekt{e}=\vekt{SC}\) in \(\vekt{f}=\vekt{SD}\). Izrazi naslednje vektorje z vektorjema \(\vekt{e}\) in \(\vekt{f}\):
   

   (a)    \(\vekt{AC}\)

   (b)    \(\vekt{CD}\)

   (c)    \(\vekt{EC}\)

   (d)    \(\vekt{DA}\)

   (e)    \(\vekt{EA}\)

   Rešitev:    (a)  \(\vekt{AC}=\vekt{e}+\vekt{f}\),     (b)  \(\vekt{CD}=-\!\vekt{e}+\vekt{f}\),     (c)  \(\vekt{EC}=2\vekt{e}-\vekt{f}\),     (d)  \(\vekt{DA}=-2\!\vekt{f}\),     (e)  \(\vekt{EA}=\vekt{e}-2\!\vekt{f}\)
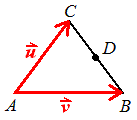3. V trikotniku \(\triangle ABC\) sta podana vektorja \(\vekt{u}=\vekt{AC}\) in \(\vekt{v}=\vekt{AB}\). Točka \(D\) je razpolovišče stranice \(BC\). Zapiši naslednje vektorje v bazi \(\vekt{u}, \vekt{v}\):
   

   (a)    \(\vekt{CB}\)

   (b)    \(\vekt{BD}\)

   (c)    \(\vekt{AD}\)

   Rešitev:    (a)  \(\vekt{CB}=-\!\vekt{u}+\vekt{v}\),     (b)  \(\vekt{BD}=\frac{1}{2}\!\vekt{u}-\frac{1}{2}\!\vekt{v}\),     (c)  \(\vekt{AD}=\frac{1}{2}\!\vekt{u}+\frac{1}{2}\!\vekt{v}\)
4. Vektorje na sliki zapiši s koordinatami:
   
   Rešitev:    \(\vekt{a}=(5,3)\),     \(\vekt{b}=(2,5)\),     \(\vekt{c}=(2,-2)\),     \(\vekt{d}=(4,-1)\),     \(\vekt{e}=(0,-4)\)
5. V koordinatnem sistemu so podane točke \(A(-2,3),~ B(5,-1)\) in \(C(4,5)\). Zapiši s koordinatami vektorje \(\vekt{AB},~ \vekt{BC}\) in \(\vekt{CA}\). Nato izračunaj vsoto \(\vekt{AB}+\vekt{BC}+\vekt{CA}\).
   Rešitev:    \(\vekt{AB}=(7,-4)\),     \(\vekt{BC}=(-1,6)\),     \(\vekt{CA}=(-6,-2)\),     \(\vekt{AB}+\vekt{BC}+\vekt{CA}=\vekt{0}=(0,0)\)
6. Točki \(A(2,-3)\) in \(B(-6,9)\) sta krajišči daljice \(AB\). Zapiši koordinati točke \(T\), ki leži na tej daljici in jo deli v razmerju \(|AT|:|TB|=1:3\).
   Rešitev:    \(T(0,0)\)
7. Dani sta točki \(A(7,0)\) in \(B(-5,2)\). Zapiši koordinate točk \(E\) in \(F\), ki delita daljico \(AB\) na tri skladne dele.
   Rešitev:    \(E(3,\frac{2}{3}),~ F(-1,\frac{4}{3})\)
8. Točka \(R(3,8)\) leži na daljici \(AB\) in jo deli v razmerju \(|AR|:|RB|=2:3\). Eno krajišče daljice ima koordinati \(A(-7,2)\). Izračunaj koordinati krajišča \(B\).
   Rešitev:    \(B(18,17)\)
9. Točka \(U\) leži na daljici \(AB\) in jo deli v razmerju \(|AU|:|UB|=2:3\), točka \(R\) pa je razpolovišče daljice \(AB\). Izračunaj koordinati točke \(R\), če poznaš točki \(U(15,9)\) in \(B(33,-3)\).
   Rešitev:    \(R(18,7)\)
10. Podane so koordinate treh oglišč paralelograma \(ABCD\):    \(A(0,-1),~ C(12,9)\) in \(D(2,7)\). Izračunaj koordinati oglišča \(B\).
    Rešitev:    \(B(10,1)\)
11. V paralelogramu \(ABCD\) poznamo oglišči \(A(-2,0)\) in \(D(0,6)\). Razpolovišče stranice \(BC\) je v točki \(F(8,5)\). Izračunaj koordinate oglišč \(B\) in \(C\).
    Rešitev:    \(B(7,2),~ C(9,8)\)
12. Štirikotnik \(ABCD\) ima oglišča \(A(-2,-1),~ B(7,5),~ C(3,7)\) in \(D(-3,3)\). Zapiši vektorja \(\vekt{AB}\) in \(\vekt{DC}\) ter ugotovi, kakšne vrste štirikotnik je to (paralelogram, trapez, deltoid …).
    Rešitev:    \(\vekt{AB}=(9,6),~ \vekt{DC}=(6,4)\). Ker je \(\vekt{AB}=\frac{3}{2}\vekt{DC}\), sta stranici \(AB\) in \(DC\) vzporedni in različno dolgi. To pomeni, da je ta štirikotnik trapez.
13. Trikotnik ima oglišča \(A(-1,6),~ B(9,8)\) in \(C(7,-5)\). Razpolovišče stranice \(AB\) označimo \(R\), težišče trikotnika pa \(T\). Zapiši točki \(R\) in \(T\) s koordinatami.
    Rešitev:    \(R(4,7),~ T(5,3)\)
14. Trikotnik \(\triangle ABC\) ima oglišči \(A(-2,3)\) in \(B(10,-7)\), težišče trikotnika pa je v točki \(T(6,1)\). Zapiši koordinati razpolovišča stranice \(AB\). Nato zapiši s koordinatama še tretje oglišče \(C\).
    Rešitev:    \(R(4,-2),~ C(10,7)\)
15. Podani so vektorji \(\vekt{a}=(8,15),~ \vekt{b}=(2,10),~ \vekt{c}=\vekt{a}+2\!\vekt{b}\).
    

    (a)   Izračunaj dolžino vektorja \(\vekt{a}\).

    (b)   Zapiši koordinati vektorja \(\vekt{c}\).

    (c)   Izračunaj dolžino vektorja \(\vekt{c}\).

    Rešitev:    (a)  \(|\vekt{a}|=17\),     (b)  \(\vekt{c}=(12,35)\),     (c)  \(|\vekt{c}|=37\)
16. V standardni ortonormirani bazi sta podana vektorja \(\vekt{a}=15\vekt{\imath}+30\vekt{\jmath},~ \vekt{b}=27\vekt{\imath}+25\vekt{\jmath}\).
    

    (a)   Izračunaj:   \(|\vekt{a}-\vekt{b}|\)

    (b)   Izračunaj:   \(|\,3\vekt{a}-2\!\vekt{b}|\)

    Rešitev:    (a)  \(|\vekt{a}-\vekt{b}|=13\),     (b)  \(|\,3\vekt{a}-2\!\vekt{b}|=41\)
17. Računsko preveri, ali sta vektorja odvisna (kolinearna) ali ne:
    

    (a)    \(\vekt{a}=(5,-2)\) in \(\vekt{b}=(15,-6)\)

    (b)    \(\vekt{e}=(8,-6)\) in \(\vekt{f}=(12,-4)\)

    (c)    \(\vekt{g}=(12,-16)\) in \(\vekt{h}=(-9,12)\)

    Rešitev:    (a)  Sta odvisna, saj je \(\vekt{b}=3\vekt{a}\).     (b)  Nista odvisna.     (c)  Sta odvisna, saj je \(\vekt{h}=-\frac{3}{4}\!\vekt{g}\).
18. Dan je vektor \(\vekt{a}=(-7,24)\). Zapiši (s koordinatama) vektor \(\vekt{b}\), ki ima enako smer in orientacijo kot vektor \(\vekt{a}\), njegova dolžina pa je 100.
    Rešitev:    \(\vekt{b}=(-28,96)\)
19. Dan je vektor \(\vekt{a}=18\vekt{\imath}-24\vekt{\jmath}\). Zapiši vektor \(\vekt{b}\), ki ima enako smer in nasprotno orientacijo kot vektor \(\vekt{a}\), njegova dolžina pa je 1.
    Rešitev:    \(\vekt{b}=-\frac{3}{5}\vekt{\imath}+\frac{4}{5}\vekt{\jmath}=(-\frac{3}{5},\frac{4}{5})\)
20. Dan je vektor \(\vekt{a}=(15,20)\).
    

    (a)   Zapiši (v koordinatah) vektor \(\vekt{b}\), ki je vzporeden vektorju \(\vekt{a}\), enako orientiran kot \(\vekt{a}\), njegova dolžina pa je za 20% večja od dolžine vektorja \(\vekt{a}\).

    (b)   Zapiši (v koordinatah) vektor \(\vekt{c}\), ki je vzporeden vektorju \(\vekt{a}\), nasprotno orientiran kot \(\vekt{a}\), njegova dolžina pa je za 20 enot večja od dolžine vektorja \(\vekt{a}\).

    Rešitev:    (a)  \(\vekt{b}=(18,24)\),     (b)  \(\vekt{c}=(-27,-36)\)
21. Dani so vektorji \(\vekt{a}=(4,-6),~ \vekt{b}=(6,7)\) in \(\vekt{c}=(10,9)\). Zapiši vektor \(\vekt{c}\) kot linearno kombinacijo vektorjev \(\vekt{a}\) in \(\vekt{b}\).
    Rešitev:    \(\vekt{c}=\frac{1}{4}\!\vekt{a}+\frac{3}{2}\!\vekt{b}\)
22. Dana sta vektorja \(\vekt{a}=(3,4)\) in \(\vekt{b}=(5,6)\). Zapiši vektor \(\vekt{\imath}\) kot linearno kombinacijo vektorjev \(\vekt{a}\) in \(\vekt{b}\), če se da.
    Rešitev:    Se da:  \(\vekt{\imath}=-3\vekt{a}+2\!\vekt{b}\)
23. Podani so vektorji \(\vekt{a}=(3,2)\), \(\vekt{b}=(-1,4)\) in \(\vekt{c}=(11,-2)\).
    

    (a)   Zapiši vektor \(\vekt{c}\) kot linearno kombinacijo \(\vekt{a}\) in \(\vekt{b}\).

    (b)   Zapiši vektor \(\vekt{a}\) kot linearno kombinacijo \(\vekt{b}\) in \(\vekt{c}\).

    Rešitev:    (a)  \(\vekt{c}=3\vekt{a}-2\vekt{b}\),    (b)  \(\vekt{a}=\frac{2}{3}\vekt{b}+\frac{1}{3}\vekt{c}\)
24. Dana sta vektorja \(\vekt{a}=(6,-5)\) in \(\vekt{b}=(3,4)\).
    

    (a)   Ugotovi, ali vektorja \(\vekt{a}\) in \(\vekt{b}\) sestavljata bazo ravnine.

    (b)   Izrazi vektor \(\vekt{c}=(27,-55)\) kot linearno kombinacijo vektorjev \(\vekt{a}\) in \(\vekt{b}\), če se da.

    Rešitev:    (a)  Vektorja sta nekolinearna in različna od \(\vekt{0}\), torej sestavljata bazo ravnine.   (b)  Se da: \(\vekt{c}=7\vekt{a}-5\!\vekt{b}\)
25. Dana sta vektorja \(\vekt{a}=(2,-6)\) in \(\vekt{b}=(-3,9)\).
    

    (a)   Ugotovi, ali vektorja \(\vekt{a}\) in \(\vekt{b}\) sestavljata bazo ravnine.

    (b)   Izrazi vektor \(\vekt{c}=(2,9)\) kot linearno kombinacijo vektorjev \(\vekt{a}\) in \(\vekt{b}\), če se da.

    Rešitev:    (a)  Vektorja sta kolinearna, torej ne sestavljata baze ravnine.   (b)  Se ne da.
26. Izračunaj realni števili \(m\) in \(n\), če veš, da sta vektorja \(\vekt{a}\) in \(\vekt{b}\) neodvisna, med njima pa velja zveza:
    

        \(m\vekt{a}+2n\vekt{b}=\vekt{a}-n\vekt{a}+6\vekt{b}\)

    Rešitev:    \(m=-2,~ n=3\)
27. Vektorja \(\vekt{a}\) in \(\vekt{b}\) sta neodvisna, med njima pa velja zveza:
    

        \(m(\vekt{a}+\vekt{b})+(n-9)\vekt{a}=2n\vekt{b}\)

    Izračunaj realni števili \(m\) in \(n\).
    Rešitev:    \(m=6,~ n=3\)
28. V kvadratu \(ABCD\) točka \(T\) leži na stranici \(CD\) in jo deli v razmerju \(|DT|:|TC|=1:2\). Izračunaj, v kakšnem razmerju daljica \(AT\) deli diagonalo \(BD\).
    Rešitev:    \(|DU|:|UB|=1:3\)
29. Dan je paralelogram \(ABCD\). Točka \(E\) leži na stranici \(AB\) in jo deli v razmerju \(|AE|:|EB|=3:1\), točka \(H\) pa leži na stranici \(AD\) in jo deli v razmerju \(|AH|:|HD|=1:2\). Izračunaj, v kakšnem razmerju daljica \(HB\) deli daljico \(EC\).
    Rešitev:    \(|ET|:|TC|=1:12\)

Skalarni produkt, dolžina, kot

30. Dana sta vektorja \(\vekt{a}=(3,1)\) in \(\vekt{b}=(2,-1)\).
    

    (a)   Nariši ta dva vektorja.

    (b)   Izračunaj dolžini obeh vektorjev.

    (c)   Izračunaj skalarni produkt \(\vekt{a}\vekt{b}\).

    (d)   Izračunaj kot med vektorjema \(\vekt{a}\) in \(\vekt{b}\).

    Rešitev:    (a)  …   (b)  \(|\vekt{a}|=\sqrt{10},~~ |\vekt{b}|=\sqrt{5}\),    (c)  \(\vekt{a}\vekt{b}=5\),    (d)  \(\varphi=45^\circ\)
31. Trikotnik \(\triangle ABC\) ima oglišča \(A(-1,2),~ B(31,6)\) in \(C(11,23)\). Točka \(P\) leži na stranici \(AC\) in jo deli v razmerju \(|AP|:|PC|=1:2\), točka \(R\) pa je razpolovišče stranice \(AB\).
    

    (a)   Izračunaj koordinate točk \(P\) in \(R\).

    (b)   Izračunaj dolžino vektorja \(\vekt{PR}\).

    Rešitev:    (a)  \(P(3,9),~ R(15,4)\),    (b)  \(|\vekt{PR}|=13\)
32. Dani so vektorji \(\vekt{a}=(2,-9),~ \vekt{b}=(3,-2)\) in \(\vekt{c}=(6,5)\). Izračunaj kot med vektorjema \(\vekt{u}=\vekt{a}+6\!\vekt{b}\)  in  \(\vekt{v}=\vekt{b}+2\vekt{c}\). Rezultat zapiši v stopinjah in minutah.
    Rešitev:    \(\vekt{u}=(20,-21),~ \vekt{v}=(15,8);~ \varphi\doteq74^\circ28'\)
33. Dana sta vektorja \(\vekt{a}=(15,-20)\) in \(\vekt{b}=(24,m)\). Določi realni parameter \(m\) tako, da bosta vektorja
    

    (a)   pravokotna,

    (b)   enako dolga.

    Rešitev:    (a)  \(m=18\),    (b)  \(m_1=7,~ m_2=-7\)
34. Podane so točke \(A(5,8)\), \(B(17,26)\) in \(C(x,2)\). Določi neznano število \(x\) tako,
    

    (a)   da bosta vektorja \(\vekt{AB}\) in \(\vekt{AC}\) pravokotna,

    (b)   da bosta vektorja \(\vekt{AB}\) in \(\vekt{AC}\) vzporedna.

    Rešitev:    (a)  \(x=14\),    (b)  \(x=1\)
35. Trikotnik \(\triangle ABC\) ima oglišča v točkah \(A(7,1),~ B(13,3)\) in \(C(x,16)\). Računsko določi neznano koordinato \(x\) tako, da bo kot \(\alpha\) v tem trikotniku meril \(90^\circ\).
    Rešitev:    \(x=2\)
36. Trikotnik ima oglišča v točkah \(A(3,1),~ B(7,4)\) in \(C(4,8)\). Izračunaj velikosti vseh treh kotov in dolžine vseh treh stranic v tem trikotniku. Ugotovi, kakšne vrste trikotnik je to.
    Rešitev:    Koti: \(\alpha=\gamma=45^\circ,~ \beta=90^\circ\),  stranice: \(a=c=5,~ b=5\sqrt{2}\). To je enakokraki pravokotni trikotnik.
37. Trikotnik ima oglišča v točkah \(A(-3,3),~ B(20,-5)\) in \(C(8,4)\). Izračunaj, koliko meri največji kot v tem trikotniku. Rezultat zapiši v stopinjah in minutah.
    Rešitev:    Največji je kot \(\gamma\doteq137^\circ56'\).
38. Pravokotnik \(ABCD\) ima stranici \(a=20~\mathrm{cm},~ b=15~\mathrm{cm}\). Točka \(T\) leži na stranici \(a\) in jo deli v razmerju \(|AT|:|TB|=2:3\). Izračunaj kot med vektorjema \(\vekt{TC}\) in \(\vekt{TD}\). Kot zapiši v stopinjah in minutah.
    Rešitev:    \(\varphi\doteq66^\circ44'\)     (Namig: Vektorja zapiši s koordinatami.)
39. Točke \(A(1,3),~ B(5,4),~ C(10,1)\) in \(D(6,9)\) so oglišča nepravilnega štirikotnika \(ABCD\). Izračunaj največji notranji kot v tem štirikotniku. (Namig: Pomagaj si s sliko.)
    Rešitev:    To je konkavni štirikotnik, \(\beta=225^\circ\)
40. Poznamo tri od oglišč paralelograma \(ABCD\):   \(B(17,-1),~ C(15,8)\) in \(D(-7,6)\).
    

    (a)   Izračunaj kot \(\alpha\) v tem paralelogramu. Zapiši ga v stopinjah in minutah.

    (b)   Izračunaj dolžino daljše diagonale.

    Rešitev:    (a)  \(\alpha\doteq97^\circ20'\),    (b)  daljša je \(f=|BD|=25\)
41. Paralelogram \(ABCD\) ima podana tri oglišča:  \(A(-3,-5),~ B(5,-2)\) in \(C(7,17)\). Izračunaj, koliko meri ostri kot med diagonalama tega paralelograma.
    Rešitev:    \(\varphi=45^\circ\)
42. Dani so vektorji \(\vekt{a}=(x,19)\), \(\vekt{b}=(63,16)\) in \(\vekt{c}=(25,60)\). Določi realni parameter \(x\) tako, da bo kót med vektorjema \(\vekt{a}\) in \(\vekt{b}\) enak kot kót med vektorjema \(\vekt{a}\) in \(\vekt{c}\).
    Rešitev:    \(x=22\)
43. Dani so vektorji \(\vekt{a}=(\frac{3}{5},\frac{4}{5}),~ \vekt{b}=(-\frac{4}{5},\frac{3}{5})\) in \(\vekt{c}=(2,1)\).
    

    (a)   Dokaži, da vektorja \(\vekt{a}\) in \(\vekt{b}\) sestavljata ortonormirano bazo ravnine.

    (b)   Vektor \(\vekt{c}\) razvij po bazi \(\vekt{a},~\vekt{b}\).

    Rešitev:    (a)  Vektorja sta enotska \((|\vekt{a}|=|\vekt{b}|=1)\) in pravokotna \((\vekt{a}\cdot\vekt{b}=0)\), torej sestavljata ortonormirano bazo ravnine.    (b)  \(\vekt{c}=2\vekt{a}-\vekt{b}\)
44. Dan je vektor \(\vekt{a}=(4,1)\). Zapiši koordinati vektorja \(\vekt{b}\), ki ima enako dolžino kot vektor \(\vekt{a}\) in je na vektor \(\vekt{a}\) pravokoten.
    Rešitev:    Dve rešitvi: \(\vekt{b}=(1,-4)\) ali pa \((-1,4)\)
45. Dan je vektor \(\vekt{u}=(7,-4)\). Zapiši oba vektorja, ki imata enako dolžino kot vektor \(\vekt{u}\) in sta na vektor \(\vekt{u}\) pravokotna.
    Rešitev:    \(\vekt{v}=(4,7)\) ali pa \(\vekt{v}=(-4,-7)\)
46. Dan je vektor \(\vekt{e}=(6,8)\). Zapiši vektor \(\vekt{f}\), ki ima dolžino 25 in je pravokoten na vektor \(\vekt{e}\). Navedi obe možni rešitvi.
    Rešitev:    \(\vekt{f_1}=(20,-15),~~ \vekt{f_2}=(-20,15)\)
47. Točki \(A(5,2)\) in \(B(11,10)\) sta oglišči kvadrata \(ABCD\). Izračunaj koordinate oglišč \(C\) in \(D\).
    Rešitev:    Dve možnosti: \(C_1(3,16),~ D_1(-3,8);~~~ C_2(19,4),~ D_2(13,-4)\)
48. Točka \(A(1,3)\) je eno od oglišč kvadrata \(ABCD\). Točka \(S(6,5)\) je presečišče diagonal tega kvadrata. Izračunaj koordinate ostalih oglišč tega kvadrata. Privzemi, da je kvadrat pozitivno orientiran.
    Rešitev:    \(B(8,0),~ C(11,7),~ D(4,10)\)
49. Vektorja \(\vekt{a}\) in \(\vekt{b}\) sta dolga vsak po 2 enoti in oklepata kot \(60^\circ\). Izračunaj skalarni produkt vektorjev \(\vekt{u}=\vekt{a}+\vekt{b}\) in \(\vekt{v}=3\vekt{a}-\vekt{b}\).
    Rešitev:    \(\vekt{u}\vekt{v}=12\)
50. Vektorja \(\vekt{e}\) in \(\vekt{f}\) sta enako dolga. Izračunaj kot med vektorjema \(\vekt{a}=\vekt{e}+\vekt{f}\) in \(\vekt{b}=\vekt{e}-\vekt{f}\).
    Rešitev:    \(\varphi=90^\circ\)
51. Dolžina vektorja \(\vekt{a}\) meri 5 enot, dolžina vektorja \(\vekt{b}\) pa meri 8 enot. Vektorja oklepata kot \(120^\circ\). Izračunaj dolžino vektorja \(\vekt{c}=\vekt{a}+\vekt{b}\).
    Rešitev:    \(|\vekt{c}|=7\)
52. Vektor \(\vekt{a}\) ima dolžino 17, vektor \(\vekt{b}\) pa ima dolžino 16 enot. Kot med vektorjema \(\vekt{a}\) in \(\vekt{b}\) meri \(60^\circ\). Izračunaj dolžino vektorja \(\vekt{c}=\vekt{a}-5\vekt{b}\).
    Rešitev:    \(|\vekt{c}|=73\)
53. Vektorja \(\vekt{e}\) in \(\vekt{f}\) sta enotska in oklepata kot \(60^\circ\). Izračunaj dolžino vektorja \(\vekt{a}=7\vekt{e}+8\!\vekt{f}\).
    Rešitev:    \(|\vekt{a}|=13\)
54. Vektor \(\vekt{a}\) ima dolžino \(\sqrt{2}\) in oklepa kot \(45^\circ\) s pozitivnim delom abscisne osi. Izračunaj \(|\vekt{a}+\vekt{\imath}|\). Rezultat naj bo točen.
    Rešitev:    \(|\vekt{a}+\vekt{\imath}|=\sqrt{5}\)
55. Vektor \(\vekt{a}\) ima dolžino 7, vektor \(\vekt{b}\) pa 2 enoti. Vektorja oklepata kot \(60^\circ\).
    

    (a)   Izračunaj dolžino vektorja \(\vekt{c}=\vekt{a}+4\vekt{b}\).

    (b)   Izračunaj kot med vektorjema \(\vekt{a}\) in \(\vekt{c}\). Zapiši ga v stopinjah in minutah.

    Rešitev:    (a)  \(|\vekt{c}|=13\),    (b)  \(\varphi\doteq32^\circ12'\)

 Domov