| - FOTOGRAFIJA |
OŠ Bežigrad
Črtomirova ul.12
1000 Ljubljana
RAZISKOVALNA NALOGA

NALOGA S PODROČJA FIZIKE

AVTOR:
Ana Vičar
Ljubljana, 2007
 | - FOTOGRAFIJA |


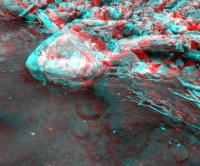
Osnova človeškega zaznavanja je vid, ki zaradi dveh očes temelji
na globinskem stereo dojemanju prostora. Osnovni fizikalni princip
globinskega, stereoskopskega ali 3D - tridimenzionalnega gledanja
je paralaksa. Z razvojem računalniške tehnologije in digitalne
fotografije, se nam je na široko odprl svet 3D fotografije.
V nalogi opisujem osnove, kako iz dveh ravninskih zamaknjenih
fotografij ustvarimo 3D sliko v naših možganih. Uporabila sem
digitalni fotoaparat, s katerim sem naredila pare zamaknjenih
slik zanimivih objektov, pokrajin, živali, ljudi. 3D učinek
sem dosegla s štirimi metodami:
* zlaganje obeh slik v rdeče - modrih odtenkih, anaglif tehnika
* zrcalno obračanje desne slike in gledanje zamaknjenih slik s pomočjo zrcala
* hitro računalniško animiranje obeh slik
* metodi sestavljanja dveh ločenih slik s prostimi očmi, paralelno
gledanje in metoda škiljenja
V nalogi je opisanih tudi nekaj drugih metod 3D zaznavanja ravninskih zamaknjenih slik. Rezultate sem podala v raziskovalni nalogi, predvsem pa na zgoščenki in internetni strani. Motivi so povzeti z vseh koncev Slovenije.
ZAKAJ SEM SE ODLOČILA ZA RAZISKOVALNO NALOGO O 3D FOTOGRAFIJI?
Kot otrok sem z veseljem prebirala bratove revije o dinozavrih, v katerih so bile tudi zelo zanimive 3D fotografije za gledanje s 3D očali. Na internetu se kakšen pojav, objekt, večkrat prikaže v 3D tehniki, obiskala pa sem tudi nekaj 3D filmskih predstav. Ko smo v družini končno kupili digitalni fotoaparat, smo prvo 3D fotografijo posneli v turškem antičnem mestu Efez. Na sliki je teater (s 3D očali glej sliko spodaj). Ker so me testni rezultati 3D fotografij pozitivno presenetili, in ko sem spoznala, da jih lahko izdelam tudi sama, sem se odločila za to raziskovalno nalogo. Odločitev je bila toliko lažja, ker smo na internetu našli nekaj brezplačnih programov za zlaganje 3D posnetkov. V nalogi sem razrešila tudi dilemo, ali je mogoča solidna prostorska fotografija zgolj z enim fotoaparatom. Kako je potekala izdelava raziskovalne naloge, boste izvedeli v nadaljevanju.
FOTOGRAFIJA JE KLASIČEN DVODIMENZIONALNI OBJEKT, NAJPOGOSTEJE NA PAPIRJU. KAKO PA JE S FOTOGRAFIJO MOŽNO PONAZORITI TRIDIMENZIONALNOST?
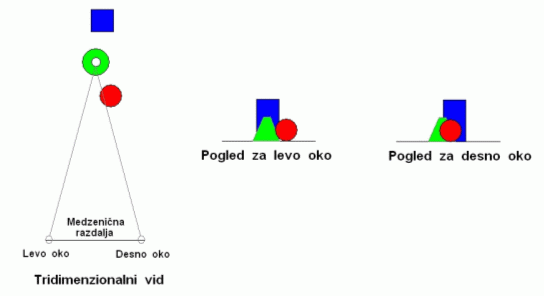
Za našo orientacijo v prostoru je potrebno znati oceniti razdaljo do posameznega predmeta v okolici. Ko predmet zagledamo, možgani-naš superračunalnik, z lahkoto izračunajo oz. določijo razdaljo od oči do predmeta. Ravno zato lahko v prvem poskusu z roko primemo nitko, naredimo ravno prav visok korak, znamo vreči kamen v tarčo. Če hočemo oceniti razdaljo do nekega predmeta, ga moramo torej opazovati z očmi. In kako vemo, kako daleč je predmet? Ker sta naši očesi razmaknjeni, vidimo z vsakim nekoliko drugačno sliko, pod drugačnim kotom. Ta pojav poznamo tudi pod imenom paralaksa. Če pogled izostrimo na določenem predmetu, zenici tvorita določen kot. Iz razdalje med zenicama in kota, pod katerim oko vidi ta predmet, lahko z malce trigonometrije izračunamo, kako daleč je opazovani predmet. In prav to trigonometrično operacijo izvedejo naši možgani.

Navidezni premik prsta glede na oddaljeno ozadje, če ga posebej pogledamo z levim in desnim očesom, imenujemo paralaksa, kot b pa je paralaktični kot prsta.
Odločilni pomen pri ocenjevanju razdalj v prostoru ima dejstvo,
da z vsakim očesom vidimo drugačno sliko. Če želimo imeti
fotografski posnetek, ki bo ponazarjal tridimenzionalnost,
moramo torej imeti dva posnetka: enega za levo in enega za
desno oko. Primer opazovanja treh predmetov v prostoru, pri
katerem je pogled izostren na srednji (prerezani stožec),
lahko vidite na skici.
Če smo v naravi sposobni določiti razdaljo med nami in v vrsto postavljenimi predmeti, tega pri tridimenzionalnem posnetku ne bo moč narediti. Posnetek je namreč narejen samo za določeno globinsko razdaljo. Zato se s pogledom ne moremo sprehajati po globini slike. Prave tridimenzionalosti zato ni mogoče narediti. Poznamo več vrst 3D fotografij. Na voljo pa je kar nekaj zvijač, kako narediti kolikor toliko verno ponazoritev tridimenzionlnosti. Za vsako od zvijač je treba posebej pripraviti fotografije, ponekod dve, ponekod pa na poseben način pripravljeno eno samo. V nadaljnjem besedilu je opisanih nekaj postopkov, nekateri so zahtevni, tudi sama vseh nisem uspela realizirati (navzkrižno gledanje slik in vzorcev mi dela težave), a prav je, da jih omenimo. Sama sem se ukvarjala predvsem z anaglifnim postopkom (izdelava 3D slik za 3D očala), metodo animacije zamaknjenih slik in metodo gledanja ene slike v zrcalu, druge pa s prostim očesom.
Navzkrižno gledanje je za mnoge najenostavnejša tehnika, a vsem ta tehnika ne uspe.

Za vajo sta nad sliko narisana dva kvadratka. Pogledate ju navzkrižno tako, da boste videli 3 kvadratke. Nikar preveč ne škilite in ne napenjajte oči, zadostuje čisto rahel navzkrižni pogled. Skoncentrirajte se na srednjega in ko bo razločno viden, boste videli sliko tridimenzionalno. Če vidite 4 kvadratke, združite srednja dva v enega in korigirajte pogled tako, da bo srednji kvadratek izostren. Poglejte na spodnjo sliko (v pomoč sta vam kvadratka) in če vidite izbočeno piramido, ki se razteza proti vam, ste pravilno izostrili pogled. Z malo vaje bo gledanje 3D slik pravi užitek. Glejte naravnost in ne preblizu.

Za gledanje stereo slik je postopek isti. Sliko navzkrižno poglejte tako, da vidite 3 slike. Osredotočite se na srednjo in uživajte.



Obstaja še ena zanimiva 3D metoda zlaganja slik. Recimo desno sliko horizontalno zrcalimo in jo rahlo odmaknemo od leve. V eni roki držimo dovolj majhno (dimenzija okrog 5x10 cm) zrcalo. Zrcalo namestimo med očesi, tik ob levem ali desnem delu nosa. Eno sliko opazujemo neposredno, drugo pa v zrcalu. Sedaj zrcalno sliko(zgornji primer), če je desna zrcaljena, z zrcalom premaknemo tako (zrcalo rahlo obračamo), da se ujame z drugo nezrcalno sliko (v našem primeru z levo sliko), ki jo opazujemo neposredno z drugim očesom (v našem primeru z levim očesom). Ko se sliki ujemata, zaznamo fantastičen prostorski (3D) učinek.
V tem odstavku bomo opisali eno od metod prikaza navidezne tridimenzionalnosti, imenovano anagliptični posnetek (anaglyph), ki ga lahko naredimo tudi sami.



Uporaba anagliptičnega postopka je najbolj razširjena različica izdelave prostorskih fotografskih posnetkov oz. 3D fotografij. Uporablja se za izdelavo 3D - posnetkov in 3D filmov.
Z dvema fotoaparatoma na medočesni razdalji posnemamo človeški globinski vid. Bistvo postopka je izdelava dveh različnih slik, ki naj bi pomenili dva različna pogleda na sliko oziroma simulirala pogled z dvema očesoma. En pogled je obarvan z rdečim odtenkom in pomeni pogled z levim očesom, posnetek za desno oko je narejen z modro ali modrozeleno barvo. Tako obdelana posnetka se nato združita v eno samo sliko, kjer sta malenkostno zamaknjena in ju lahko opazujemo na zaslonu ali barvno natisnemo na papir. Medsebojna lega obeh posnetkov bo določila »središče globinske ostrine«; to je tisto področje v prostoru, pred in za katerim so objekti, ki jih želimo videti, kot da bi bili v prostoru. Ko tako pripravljen posnetek natisnemo, tega področja ni več možno spremeniti. Še več, pri »slabo« izbranem motivu so lahko deli posnetka, ki so zunaj »središča« globinske ostrine, moteči, kajti rdeča in modra slika sta lahko med seboj preveč zamaknjeni. Del posnetka, ki je namenjen »izostritvi« pogleda, je lahko natisnjen v črno-beli ali barvni tehniki.

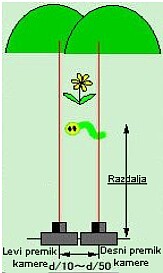
Slika zgoraj prikazuje razmik med fotoaparatoma glede na oddaljenost predmeta.
Premik fotoaparata med fotografiranjem je načeloma enak medočesni razdalji,
vendar je ta premik lahko tudi drugačen in je odvisen od oddaljenosti predmetov.
Če recimo od blizu slikamo rože za 3D predstavitev, bo ta premik manjši, vendar
v enakem razmerju glede na razdaljo, kot je to pri normalnem gledanju velikih
teles (v grobem velja, da je razdalja med očesoma/oddaljenost_3m = premik/oddaljenost_predmeta).
Premik je tudi odvisen od 3D učinka, ki ga želimo doseči – želimo si recimo,
da nam nek predmet (kip) navidezno izstopa iz 3D projekcije.
Obstaja dokaj dobra ocena zamika fotoaparata, baze D.
Zamik fotoaparata D je enak 30-tini ali 40-tini razdalje do najbližjega objekta, velja za
objektive gorišča f = 50 mm in klasični 35 mm-ski film. Če pa uporabljamo drugačni objektiv,
pa dobljeno številko ponožimo še s kvocientom med 50 mm in goriščem (v mm) objektiva našega fotoaparata:
D = (L/40)*(50/f[mm]). Primer - če uporabljamo objektiv gorišča f = 100 mm in bi radi
dobili 3D učinek za objekt oddaljen 40 m, velja: D = (40m/40)*(50/100) = 1m*0.5 = 0.5m = 50 cm.
Aparat bomo torej horizontalno zamaknili za pol metra.
Enačba za zamik [ D = (L/40)*(50/f[mm]) ] je moja (Anina enačba),
saj je ni nikjer zaslediti v tej obliki:
Anina enačba: D = (L/40)*(50/f[mm])
Večinoma je podano priporočilo, da je D kar razdalja do predmeta deljena s 40 ali 30,
a to velja samo za objektive 50 mm.
Kako pa korektno
določimo, izračunamo premik, bomo pokazali v nadaljevanju, v poglavju
"IZPELJAVA ENAČBE ZA IZRAČUN BAZE D".
Tako natisnjeno fotografijo (ali film v kinu) je treba gledati skozi za to namenjena očala, ki imajo na levi strani rdeč, na desni pa moder (oz modrozelen) filter. Ker sta rdeča in modra barva komplementarni, bo skozi rdeč filter opazovana modra barva oz. skozi moder filter opazovana rdeča barva videti črna. Tako bo vsako oko videlo »svoj« del posnetka.
KAKO DO 3D FOTOGRAFIJ?
Za izdelavo 3D-fotografij so namenjeni posebni fotoaparati, ki naredijo za eno 3D sliko dva posnetka, enega za pogled z levim in enega za pogled z desnim očesom. Takšni fotoaparati imajo bodisi dva objektiva ali pa sta to dva fotoaparata, združena v enega. Pri vseh takšnih fotoaparatih je bistveno to, da je razdalja med objektivi približno enaka razdalji med zenicama, to je približno 65 do 70 mm. Če je ta razdalja manjša ali večja, dobimo v splošnem slabše rezultate. Mnenja glede razdalje med objektivi se razhajajo, vse pa je seveda odvisno od gorišča in oddaljenosti objektov in ozadja. Za objektive goriščne razdalje 50 mm in predmete razdalje okrog 3 m na zelo oddaljenem ozadju je optimalen razmik med objektivoma res enak medočesni razdalji, 65 do 70 mm, kar pomeni paralaktični kot okrog 1.3 stopinje. Na filmu je to razlika okrog 1,2 mm v legi 3 m oddaljenih motivov glede na levi in desni fotoaparat. Pomembna je tudi maksimalna razdalja med posnetkoma na filmu na združeni 3D sliki, ponavadi je okrog 1.2 mm za film 35 mm. Še enostaven recept za slikanje z enim fotoaparatom kar iz roke, za normalen objektiv (50 - 60 mm) in nekaj metrov oddaljene objekte: Dobra tehnika je, da težo prenesete iz ene noge na drugo. Tako se boste premaknili ravno tistih 6 cm. Zadnja stavka sta povzeta iz: http://www.e-fotografija.com/artman/publish/article_790.shtml, Matjaž Humar.

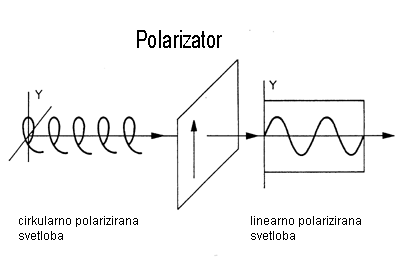
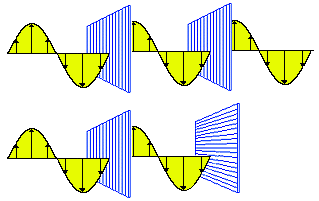
Digitalni fotoaparati omogočajo neskončno igranje s posnetki. Zato si lahko tudi sami omislimo izdelavo 3D-fotografij. Najprej naredimo posnetek za eno oko, nato fotoaparat prestavimo v desno za približno 60 do 70 mm in naredimo posnetek še za desno oko. Pri tem je nadvse pomembno, da fotoaparata ne zasučemo in ne spreminjamo nastavitev (npr. zuma, bliskovke, svetlobe …) ali premikamo po višini. Še najpreprosteje bi bilo, če bi imeli v L oblikovano vodilo iz plastike ali pločevine, na njem pa označeno »medzenično« razdaljo. Med fotografiranjem tega vodila ne smemo premikati! Nato je treba posnetke obdelati tako, da posnetku za levo oko dodamo rdeči ton (oz. odvzamemo modri ton), posnetku za desno oko pa dodamo modri ton (oz. odvzamemo rdeči ton). To bi lahko naredili s kakšnim programom za obdelavo slik. Nekateri programi znajo celo sami iz dveh posnetkov narediti anagliptično fotografijo. Na voljo so tudi galerije s številnimi anagliptičnimi posnetki. Na strani: http://www.stereoeye.jp/gallery/world/18/index_anae.html , so povezave na svetovno najbolj znane 3D stereo spletne galerije. Uporaba polarizatorjev. Sliki lahko ločimo tudi s polarizatorjema (zasukanima za 90 stopinj, recimo pred diaprojektorjema) in ju nato projecirani na platno gledamo skozi polarizacijska očala. Ta metoda se veliko uporablja, tudi v 3D kinih – v Ljubljani od leta 2005. Ta metoda je najboljša, ker se ohranijo barve in veliko svetlobe.



V Sloveniji obstaja tudi društvo za 3D fotografijo (Stereoskopsko društvo), vodi ga gospod Matija Vidmar, sin svetovno znanega in cenjenega slovenskega elektrotehnika in šahista dr. Milana Vidmarja. Društvo prireja imenitne projekcije v Cekinovem gradu – Ljubljana.
3D OČALA
Za gledanje anagliptičnih fotografij so potrebna rdeče-zelena (modrozelena) očala.

NA KAJ PAZITI PRI IZDELAVI POSNETKOV?
Ker je treba narediti dva posnetka z enim fotoaparatom, ni mogoče narediti posnetkov premikajočih se predmetov. Še več, če je na enem posnetku nekaj, česar na drugem sploh ni (npr. odstranjena vaza), bo to na posnetku moteče. Ne delajte 3D-posnetkov objektov, ki so zelo daleč (npr. gore), ker bosta posnetka praktično enaka. Če pa je slikani objekt zelo blizu (npr. pol metra), bosta ozadje in ospredje tega objekta preveč »raztresena«, kajti razdalja je primerljiva z medzenično razdaljo. Najbolje bo, če fotografirani objekt miruje. Naj bo nekaj objektov v ospredju in nekaj v ozadju. Objekt naj bo oddaljen kakšen meter – a kot bomo videli, so mogoča tudi drugačna razmerja.
Anaglif je lik, izdolben v plitkem reliefu. Ista beseda pomeni mirno sliko ali film, ki ga sestavljata dva rahlo različna pogleda na isti objekt, na posnetku prikazana tako, da sta natisnjena v dveh komplementarnih barvah. Običajno je en posnetek pobarvan z rdečim, drug z modrozelenim odtenkom. Če imamo očala, dobimo pri gledanju takšnega posnetka občutek prostornosti. Pojem »glyph« najdemo tudi pri besedah »hieroglif« (v kamen vrezana staroegipčanska pisava), »gliptika« (umetniški izdelki iz poldragih kamnov, kovine ali stekla z vrezano ali reliefno podobo), »gliptoteka« (zbirka kiparskih del)…

GEOMETRIJSKA OPTIKA IN FOTOAPARAT
Vemo, da je nepogrešljiv del fotoaparata objektiv, ki tvori
sliko na filmu ali CCD čipu. Zato nekaj besed o optiki, lečah,
nastanku slike, ne bo škodilo.
1. Enačba tanke zbiralne leče
Zbiralna (konveksna)
leča

Naj bo a > f.
Slika predmeta je obrnjena in realna, saj sliko lahko projeciramo na platno ali film, lahko pa jo tudi opazujemo skozi drugo lečo (lupo) in tako ustvarimo teleskop ali mikroskop.
Slika 1.1
Za izračun razmerja med velikostjo predmeta in slike, razdalje (a) predmeta od optične ravnine in razdalje (b) slike od predmeta zadostujeta dva žarka.
Žarek 1 potuje od konice predmeta k leči vzporedno z optično osjo.
Žarek 2 potuje od konice predmeta k leči skozi geometrijsko središče.
F -gorišče leče
f -goriščna razdalja leče
Poiščimo povezave med a, b, p, s in f s pomočjo podobnih trikotnikov (slika 1.1).
1.1) 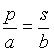 1.2)
1.2) 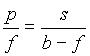
Če enačbi med sabo delimo in nekoliko preoblikujemo, dobimo enačbo 3, ki ji tudi pravimo enačba zbiralne leče (v našem primeru je a > f).
deljenje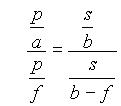 sledi
sledi
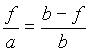 sledi
sledi 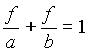
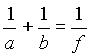
Če je razdalja (a) do predmeta zelo velika, potem približno velja: 1/a=0 ,kar pomeni, da slika nastane zelo blizu gorišča, brez velike napake velja: b=f
Kje torej nastane slika oddaljenega objekta v fotoaparatu ali teleskopu in zakaj?
3.1. Fotoaparat
Fotoaparat je optično-mehanični-elektronski sistem, ki predmete preslika na film ali elektronski polprevodniški senzor, CCD (Charge Coupled Device - naprava za zbiranje naboja, ki se sprosti ob vpadu svetlobe na polprevodnik) čip. Slika na filmu je obrnjena, realna in ponavadi pomanjšana. Fotoaparat je sestavljen iz objektiva (slika 3.1), kateri projecira odbito svetlobo ali svetlobo emitirano od realnih predmetov na film in časovnega mehanizma za proženje, ka
teri odmakne zaveso pred filmom, da se le ta osvetli.Objektiv je sistem leč z vgrajeno spremenljivo vhodno odprtino, ki odloča o zaslonki. Zaslonka je razmerje (kvocient) med goriščno razdaljo (f) in vhodno odprtino (D), velja: zaslonka=f/D (vrednosti so ponavadi od 2,8 do 22). Manjša je vrednost zaslonke, večji je premer vhodne odprtine D, več svetlobe pade na film, film je bolj osvetljen in obratno. Razmerje (kvocient) med vhodno odprtino (D) in goriščno razdaljo (f) je relativna odprtina: D/f. Relativna odprtina je tudi obratna vrednost zaslonke: 1/zaslonka=1/(f/D). Osvetlejnost filma je sorazmerna s kvadratom relativne odprtine (D/f)2=(1/(f/D))2.
Z vrtenjem objektiva ostrimo sliko, to je spreminjamo razdaljo b, ki je ponavadi le nekoliko večja od f, za zelo oddaljene predmete je razdalja b kar enaka f. Globinska ostrina se zelo poveča, če je vhodna odprtina zaprta (zaslonka 11 ali 16). V astronomiji potrebujemo odprtine velikih premerov, da ulovimo več prihajajoče svetlobe, ki je ponavadi šibka, ker so vesoljska telesa zelo daleč.Objektiv je, na kratko, zbiralna leča (sestavljena iz večih leč), kjer je a>f in veljajo zgornje enačbe.
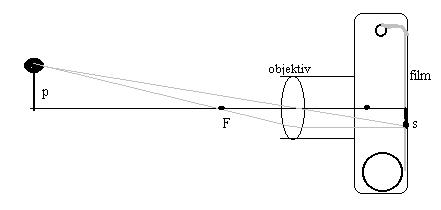
Slika 3.1
Zastavimo si nekaj vprašanj!
Na kateri razdalji tvori objektiv realno sliko?
Kako izračunamo velikost slike, ki jo tvori objektiv, če poznamo goriščno razdaljo objektiva in zorni kot zelo oddaljenega telesa, in če je zorni kot zelo majhen. Iz spodnje slike lahko razberemo, da je računanje velikosti slike, ki jo tvori objektiv, kar enako računanju loka na krogu. Razlaga! Če je lok na primer kar obseg kroga, potem velja: O=2p r=j r,j =kot, ki meri 2p radianov, to je 6,28radianov.
Torej je 2p radianov=360o, ali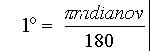 ;
;
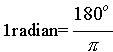 .
Ker je pri majhnih kotih tetiva skorajda enaka loku, je
naša trditev utemeljena, glej sliko 3.4.
.
Ker je pri majhnih kotih tetiva skorajda enaka loku, je
naša trditev utemeljena, glej sliko 3.4.
lok=jr
če j
<5o potem je tetiva približno enaka loku.Torej velja:
| S=j *f | -če zamenjamo lok s sliko (s) in r z goriščem (f) |
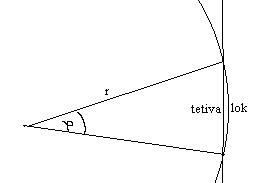

Slika 3.4
Primer:
Kot pod katerim vidimo Luno je j =30', goriščna razdalja objektiva (teleskopa) naj bo f=500mm. Kako velika slika nastane na filmu?
slune=j f
j pretvorimo v radiane (upoštevamo, da je 1o=60'): radianov
radianov
REZULTAT: s=4,4mm, kar je že solidna velikost.
Opomba: radianov ponavadi ne zapisujemo.


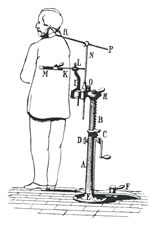
 Aristotel |
 Camera obscura |
 Leonardo da Vinci |
 Camera obscura |

 Joseph Nicephore Niepce |
 Joseph Nicephore Niepce - Pogrnjena miza, 1822 - prva fotografija |


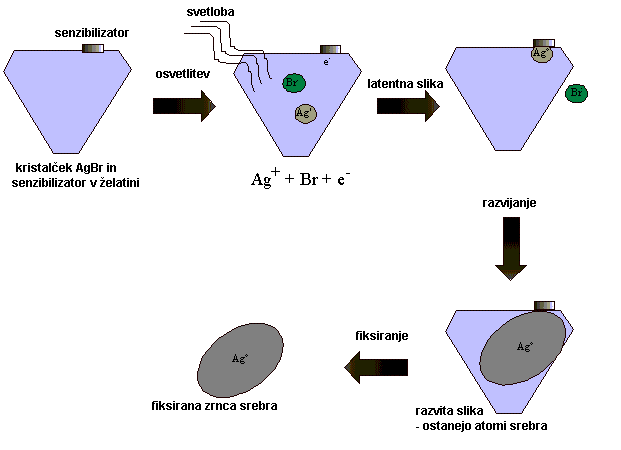
Ag+ + e- ® Ag0
Bron z razvijanjem odstranimo in nato s fiksirjem še senzibilizator.






|

|
 | 
|
 | 
|
|



 Dr. KAREL GROSSMAN (1864 - 1929) odvetnik, filmski amater, kulturni delavec… |
 Karel Grossman: Odhod od maše v Ljutomeru, Lotmerku (1905) |







 Julij Nardin (1877-1959) |
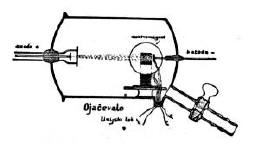 Nardinova vakuumska elektronka kot ojačevalnik po skici iz leta 1929 |
 Izumitelj Anton Codelli (1875-1954) |
 Codellijeva televizija po razpravi iz leta 1930 |


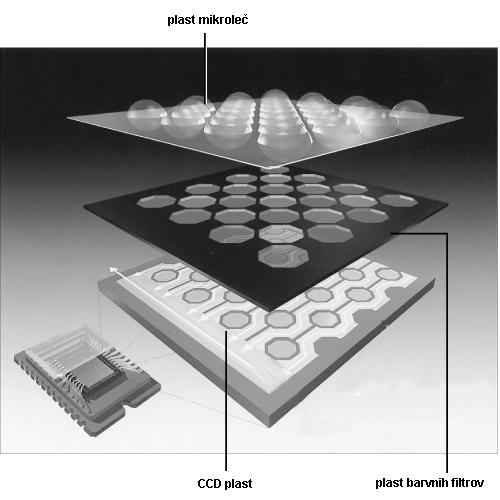
Fotodiode so razporejene
po CCD-ju ena poleg druge v ravno vrsto, vrste pa ena nad
drugo. Tako dobimo nekakšno matriko (m x n) elementov,
ki se običajno imenuje kar optična ločljivost
fotoaparata. Kakovostnejši fotoaparati imajo preko
milijon fotodiod, tisti malce slabši pa za polovico manj.
Zaradi narave razporeditve fotodiod je tudi rezultat v
obliki matrike. Slika za računalniško obdelavo, naj bo
fotografirana s klasičnim aparatom in nato skenirana ali
pa posneta z digitalno kamero ali fotoaparatom, je raster
sestavljen iz kvadratkov različnih barv in svetlosti. Ti
kvadratki so razporejeni po sliki tako kot fotodiode po
enoti CCD. Če ima ta slika dovolj kvadratkov (vemo že,
da imajo kakovostnejši CCD-ji preko milijon fotodiod) in
to sliko pogledamo iz
dovolj velike razdalje, naše oko sestavi vse te
kvadratke (pike, piksle, svetlobne elemente) v prepoznavno
, originalu podobno sliko. Tu
vidimo, zakaj je pomembno število fotodiod na enoti CCD.
Več kot jih je, več detajlov bo na posneti sliki in
bolj jo bomo lahko
povečali.


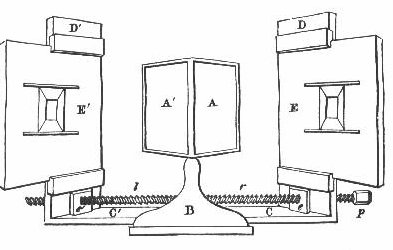

|
|

|









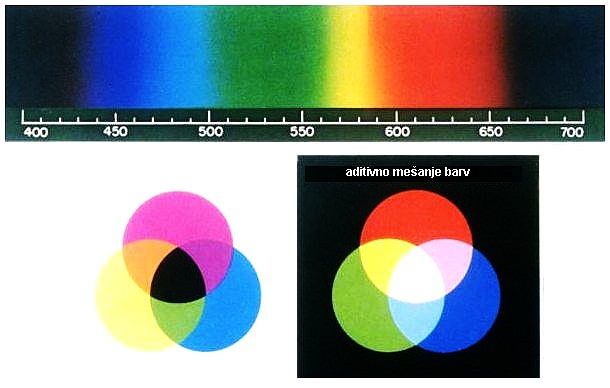
Kaj je svetloba in kako deluje oko?
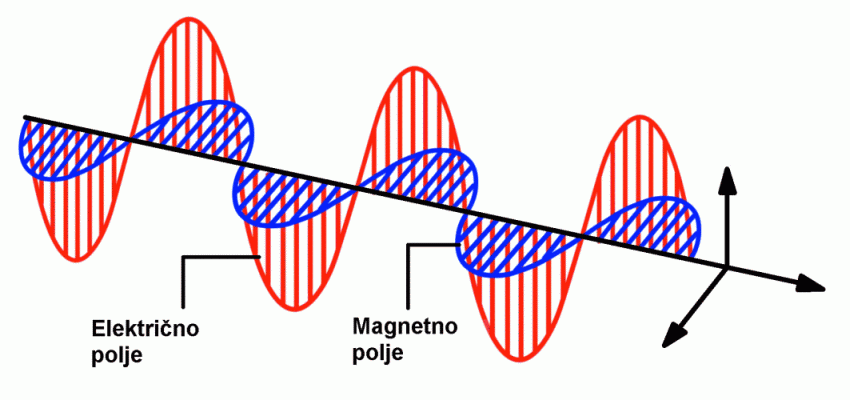
Elektromagnetno valovanje je valovanje električnega in magnetnega polja.
Električno in magnetno polje valujeta v smeri pravokotno eno na drugo in
vzdržujeta druga drugo. V prostoru se elektromagnetno valovanje širi s
hitrostjo c = l*n = 300.000 km/s v smeri pravokotni na smer električnega in
magnetnega polja. Elektromagnetno valovanje prenaša gibalno količino
in energijo, pri čemer je polovica te shranjena v električnem polju,
druga polovica pa v magnetnem polju.
 |
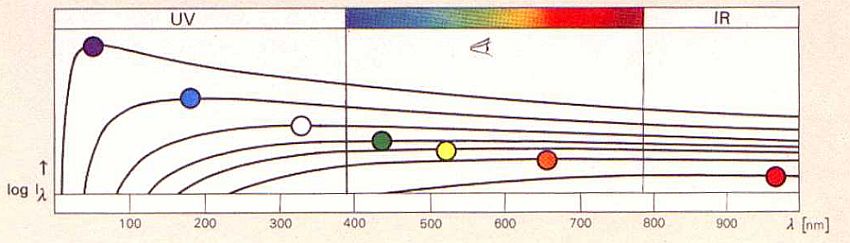 |

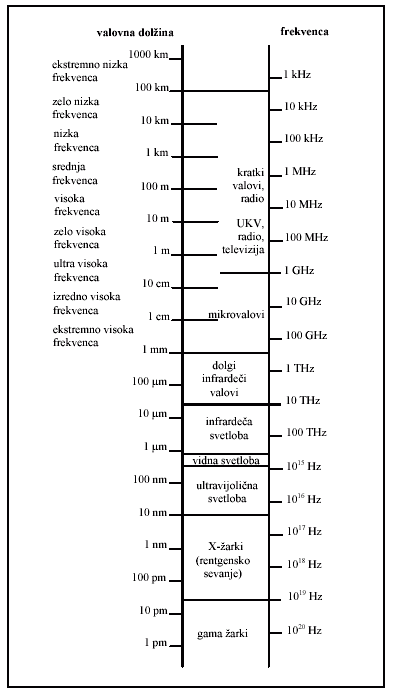
Elektromagnetno valovanje z valovnimi dolžinami med 380 nm in 740 nm zaznavamo kot svetlobo (nanometer [1 nm] = 10-9 m). Svetloba se širi v energijskih paketih, imenovanih kvanti ali fotoni, energija katerih je odvisna od frekvence n elektromagnetnega valovanja (Energija = hn , h je Planckova konstanta - h = 6.626 × 10-34 Js). Svetlobo – fotone - izsevajo pospešeni nabiti delci ali atomi, molekule, ko prehajajo z višjega energijskega stanja v nižje energijsko stanje.

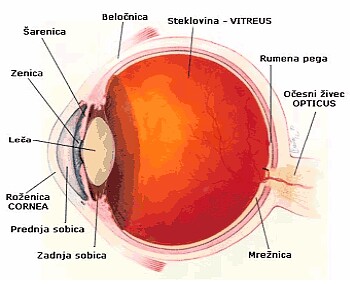
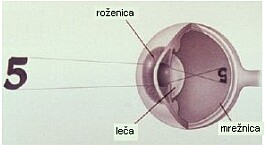
OKO
Čutilo, ki zaznava emitirane ali odbite fotone od predmetov,
tekočin, itn, je oko. Bistvena dela očesa sta leča in mrežnica.
Leča opravlja vlogo objektiva pri fotoaparatu, mrežnica pa filma
ali CCD čipa. Na mrežnici so fotoreceptorji (čepki - barvno
gledanje čez dan in palčke - črno, belo gledanje v mraku).
Fotoni povzročijo dražljaj, ki ga zaznajo receptorji, ta
pa potuje po očesnem živcu v možgane in ti tvorijo sliko.
Možgani sliko obrnejo pokonci, na mrežnici je namreč
zasukana za 180° – enako kot na filmu.
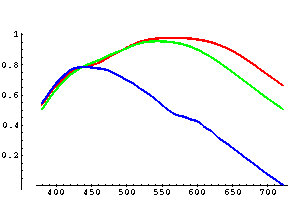
Paličic je v očesu okoli 10 milijonov, medtem ko je čepkov manj – 6 do 7 milijonov.
Loči jih tudi senzorični prag, saj lahko paličice zaznajo veliko manjšo količino
vpadne svetlobe kot čepki – zato ob majhnih svetlostih slabo zaznavamo barve.
Čepkov je največ na delu mrežnice, ki se imenuje rumena pega in se nahaja točno
nasproti očesne leče. Tukaj zaznavamo barve svetlobe najbolje, saj se sem preslika
točka, kamor smo usmerili pogled. Ob straneh rumene pege se koncentracija čepkov
zmanjšuje na račun koncentracije paličic. Pod rumeno pego se nahaja stičišče
vidnega živca in mrežnice – to je mesto, kjer čutnih celic ni in posledično
vpadne svetlobe tukaj
ne zaznamo.

IZPELJAVA ENAČBE ZA IZRAČUN BAZE D - RAZDALJE MED FOTOAPARATOMA
Enačba se glasi:
k * (Lmax * Lmin) / (Lmax - Lmin) Stereo_baza D = --------------------------------------- f
D – je stereo_baza, zamik aparata ali razdalja med objektivoma
k - je maksimalni zamik (maksimalna vrzel) leve in desne slike na
sestavljenem posnetku, filmu
f - je goriščna dolžina (razdalja) objektiva
Lmin - je razdalja do najbližjega objekta v motivu
Lmax - je razdalja do najoddaljenejšega objekta v motivu
- velja, če je razdalja Lmin precej večja od gorišča f !!!!!
Kako pa pridemo do enačbe?
Kot smo že povedali, je človeško oko, skupaj z možgani, z evolucijo prilagojeno za prostorsko gledanje s pomočjo paralakse. Izkaže se, da je maksimalen še neobremenjujoči paralaktični kot b okrog 1,3 stopinje, v radianih je to b = 1.3°*b/180° = 0,023. Seveda gledamo tudi bližje objekte, a to na daljše obdobje zahteva večji napor, čeprav je optimalna bližnja razdalja xo, na kateri vidimo največ podrobnosti, zgolj 25 cm. Oglejmo si, kolikšen zamik slik povzroči paralaksa 1,3° na filmu. Vse je odvisno od gorišča. Objektivi so ponavadi v osnovi goriščne razdalje f = 50 mm in prikazujejo sliko v taki obliki, kot jo vidimo ljudje s svojimi očmi (vidno polje človeškega očesa nekako 46 stopinj). Sliko zato tudi načeloma najmanj 'popačijo'. Razpon goriščne razdalje je od 45 – 60 mm, vendar je 50 mm najbolj standarden objektiv. Včasih so vse zrcalnorefleksne fotoaparate prodajali z objektivi 50 mm.
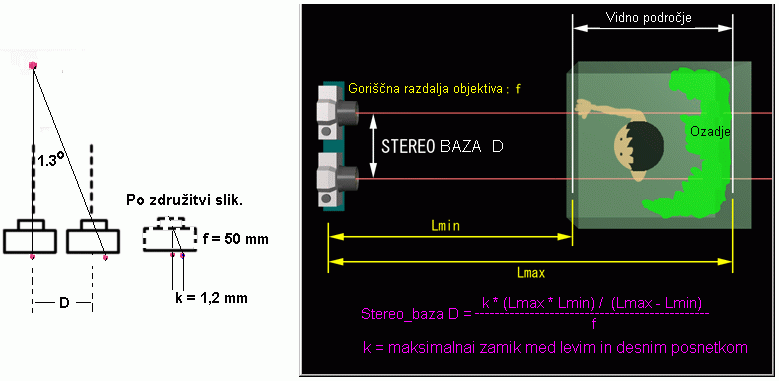
Kolikšen pa je torej zamik k obeh slik (maksimalna vrzel) pri goriščni razdalji objektiva f = 50 mm? Ker je paralaksa majhna in je Lmin preceje večja od f, velja kar zveza k = f* b = 50mm*0,023 = 1,2 mm.
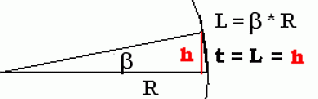
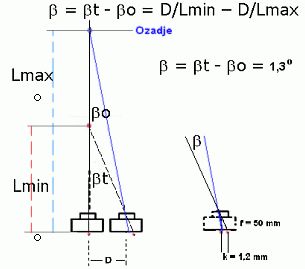
Če temu približku ne verjamemo, se lahko o njegovi veljavi prepričamo z merjenjem dolžine loka in tetive pri majhnih kotih, nekaj stopinj – izkaže se, da je v tem primeru razlika med dolžino tetive in loka minimalna. Vrnimo se k enačbi. Kaj pa se zgodi, če bi radi dobili 3D sliko za oddaljene objekte in uporabljamo daljše goriščne razdalje, ali pa je ozadje slikanega objekta, telesa, zelo blizu? Najprej odgovor na zadnji del vprašanja in preko njega bomo prišli do vseh odgovorov. Če je ozadje relativno blizu, bomo zamik D toliko povečali, da bo razlika kotov med zamikom telesa (bt = D/Lmin) in zamikom ozadja (bo = D/Lmax) spet enaka 1,3°, kar seveda ustreza našemu paru oči.
b = bt - bo = D/Lmin – D/Lmax = D*(Lmax - Lmin)/(Lmin*Lmax) = 1,3°
ker velja, da je k = f* b, bomo po vstavitvi zgornje enačbe za b dobili iskano rešitev:
k = f* D*(Lmax - Lmin)/(Lmin*Lmax)
k * (Lmax * Lmin) / (Lmax - Lmin) Stereo_baza D = --------------------------------------- f - velja, če je razdalja Lmin precej večja od gorišča f !!!!!
Seveda lahko zamik slik k iz 1,2 mm povečamo na večje vrednosti in
tako dobimo močnejši 3D učinek, a ne gre pretiravati, saj ima adaptacija oči,
škiljenje, svoje meje.
Iz povedanega sledi, da moramo paziti, kako blizu je najbližji motiv 3D slikanja,
saj se lahko zgodi, da bomo del slike videli 3D, bližnji objekti pa bodo preveč
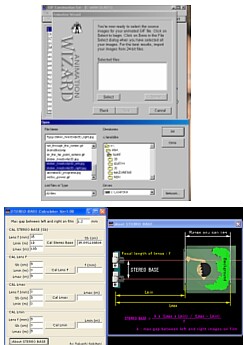
zamaknjeni. Masko za izračun baze D ali ostalih spremenljivk, sem vključila na
internetno stran, kot del naloge in kot pomoč vsem, ki bi se radi resno ukvarjali
s 3D fotografijo, naslov Stereo kalkulatorja je:
http://www2.arnes.si/~lkkpcj1/fotografija3d/stereo_baza1.html
Zgornja enačba velja, če je razdalja bližnjega predmeta,
Lmin, veliko večja od gorišča aparata f.
Za makro fotografije, kjer je Lmin že primerljiva z f,
recimo rožic, itn, pa bolje velja splošna, univerzalna zveza - približek.
Izpeljava je podobna zgornji (le razdaljo f nadomestimo z b iz enačbe za tanke leče
[1/a + 1/b = 1/f],
saj slika sedaj ne nastane v gorišču f, ampak na razdalji b, glej poglavje o tankih lečah).
1/b = 1/f -1/a
- sedaj velja, da je k = b* b,
po vstavitvi že znane enačbe za b
dobimo:
b = D/Lmin - D/Lmax = D*(Lmax - Lmin)/(Lmin*Lmax) - enako kot zgoraj,
dobimo naslednje povezave:
k * Lmax *(Lmin ) k * Lmax *(Lmin ) Stereo_baza_uni D = ------------------- = ----------------- *(1/f - 1/a) (Lmax - Lmin) * b (Lmax - Lmin) Kateri a izbrati (razdaljo ostrenja), izkaže se, da je zaradi globinske ostrine nabolje izbrati a, pri katerem je kot točke ostrenja (bos) enak polovici vsote kotov bližnjega telesa in ozadja: bos = (bt + bo)/2 - ker velja: bt = D/Lmin in bo = D/Lmax - kot točke ostrenja pa je: bos = D/a - če upoštevamo zgornje povezave, dobimo: D/a = (D/Lmin + D/Lmax)/2 1/a = (1/Lmin + 1/Lmax)/2 1/a = (Lmax+Lmin)/(Lmin*Lmax*2) - iz česar sledi: a = 2*Lmax*Lmin/(Lmax+Lmin) k * Lmax *(Lmin ) k * Lmax *(Lmin ) Stereo_baza_uni D = ----------------- *(1/f - 1/a) = ----------------- *(1/f - (Lmax+Lmin)/(Lmin*Lmax*2) ) (Lmax - Lmin) (Lmax - Lmin) - zgoraj smo izpeljali Bercovitz-evo enačbo za bazo D - za Lmax neskončno velja: Stereo_baza D = k*(Lmin/f - 0.5) - za Lmin veliko večje od f, pa velja že znana povezava spodaj: k * Lmax*Lmin Stereo_baza D = -------------------- (Lmax - Lmin) * f
Izračun za univerzalno zvezo, torej tudi za makro, je pod točko 3, vključen v Stereo kalkulator:
http://www2.arnes.si/~lkkpcj1/fotografija3d/stereo_baza1.html
Zakaj ni nujno, da je maksimalni zamik k na filmu zmeraj enak, torej 1,2 mm?
Problem je, ker so formati filmov in čipov različni, kar lahko pomeni prevelik
ali premajhen zamik slik pri povečavah na platnu. Kako določimo k? Pomembno je
razmerje stereo ločenosti (RSL), to je relativni zamik slik na projekcijskem
platnu, ekranu, izražen z razmerjem med dejanskim zamikom slik na platnu in
širino ekrana. Za k velja spodnja povezava.
k= širina filma (mm) * RSL
Recimo, če imamo 2 m široko platno, je potreben zamik slik na platnu, pri gledanju na razdalji dobrih treh metrov, nekje 70 mm (paralaksa 1,3°), RSL je torej 70mm/2000mm = 0.035 = k/Širina_filma. Maksimalna vrzel med slikama, zamik k je torej za 35 mm film enak 35(mm) * 0.035 = 1.2 mm. Za drugačne formate, ccd čipe, filme, pa moramo pri izračunu k-ja upoštevati njihove širine. Problem gledanja 3D slik je lahko tudi razdalja do ekrana, platna, sploh pri večjih dvoranah.
Uporabljala sem digitalni fotoaparat (OLYMPUS 6.0 MEGAPIXEL/ SP-500 UZ),
osebni računalnik, ogledalo, program za animiranje GIF CONSTRUCTION SET
(program je plod podjetja Alchemy Mindworks Inc. iz Kanade, je prosto
dosegljiv preko medmrežja) in brezplačni program za tvorjenje dvobarvnih
zamaknjenih slik ANAGLYPH MAKER (program je dosegljiv preko medmrežja na
strani:
http://www.stereoeye.jp/software/index_e.html
, avtor Japonec
Takashi Sekitani), 3D očala (kupljena preko medmrežja v ZDA) in samo medmrežje.
Na omenjenem naslovu se tudi dobi program 3D Slide Projector za 2 LCD
projektorja, z veliko ostalimi možnostmi. Digitalni fotoaparat sem v
glavnem v časovni stiski zamikala ročno, glede na oddaljenost objektov.
Zelo dober 3d program je tudi (dodatno omogoča rotacijo, itn)
StereoPhoto Maker iz:
http://stereo.jpn.org/eng/stphmkr/
Program ANAGLYPH MAKER je zelo enostaven. Izbereš si levo in desno sliko, barvno ali črno-belo opcijo zlaganja, barve in ozadje, izvedeš združevanje slik, nakar jih zamakneš glede na napake pri slikanju in shraniš – lahko kot anaglif za gledanje s 3D očali, ali kot ločeni korigirani sliki za škiljenje, zrcaljenje ali projekcijo preko polarizatorjev. Barva 3D fotografija ni zmeraj uporabna, sploh če v njej prevladujejo izraziti rdeči in zeleni odtenki. ANAGLYPH MAKER vam omogoča takojšnje testiranje različnih možnosti zlaganja, črno-belo, barvno, za različne filtre. Programu bi zelo koristile še možnosti rotacije slik, spreminjanja velikosti, izdelava gif animacij.

Program GIF CONSTRUCTION SET je namenjen izdelavi gif animacij, s katerim sem animirala nekaj parov slik – glej animacije na spletu. Hitra ponavljajoča izmenjava slik, čas lahko v programu nastavimo, nam da zelo učinkovit prostorski (3D) učinek.


Kaj vse sem fotografirala?
Fotografirala sem arhitekturo Ljubljane (arhitekturo Jožeta Plečnika, cerkve, ulice, spomenike,...), Hrastovlje (tabor, freske...), Koper (prstanišče, ladje, ulice, obalo...), dolino Soče (korita, trdnajvo Kluže...), Kog (naravo, živali, kmetijski stroji...), Bled (jezero z okolico), ljubljanski živalski vrt (živali), Ajdovski Gradec nad Vranjem pri Sevnici (ostanki naselbin staroselcev)... Vsaj polovica slik je posvečena slovenski kulturni dediščini, ki se nekako izgublja v uvoženi turbo kulturi in kulturni politiki.
Kako gledamo 3D fotografije?
Nadenemo si rdeče - zelena očala. Pogled upremo v fotografijo in za nekaj trenutkov počakamo, da se oči navadijo na globino slike. Še boljša globinska zaznava pa je takrat, kadar spremenimo položaj telesa rahlo v levo ali desno.
Sledijo rezultati - slike narejene v okviru raziskovalne naloge – zadnjih nekaj slik je iz drugih virov, ki so navedeni ob slikah.
REZULTATI - glej slike pod literaturo
Zelo veliko 3D slik izdela vesoljska agencija NASA, tudi na spletni strani APOD
(Astronomy Picture of the Day:
http://antwrp.gsfc.nasa.gov/apod/
) jih najdemo veliko,
kar samo kaže na sugestivno moč 3D predstavitev.




Z rezultati sem zelo zadovoljna. Predvsem me je veselilo, ker je večina ljudi, ki si je ogledala slike, bila presenečena nad izjemno slikovitostjo, ki jo nudi prostorska fotografija. Nekateri so izjavili, da je 3D fotografija navidezno še bolj globinsko preprečljiva kot sama realnost zaznana s prostima očesoma. Kakor se zdi postopek za izdelavo prostorske fotografije zelo preprost, pa vendar vzame ogromno časa, sploh če želimo doseči kvalitetne rezultate. Največji problem moje metode je bil, da nisem uporabljala dveh aparatov na skupnem stojalu, kar je običaj pri profesionalni 3D fotografiji. To so mi onemogočale predvsem finančne in časovne razmere. Zaradi tega sem zelo težko fotografirala živali in premikajoče se objekte. Pri 3D fotografiji, to so lastne ugotovitve, je zelo pomembna izbira motiva - Plečnikova arhitektura, torej tudi antična, se je izkazala kot izjemno primeren motiv za globinsko fotografijo (stebri, loki, amfiteatri). Pomebno je tudi, da motiv nima težišča na robovih, levo ali desno, da je centralno lociran. Pri motivih je zelo pomembno, da je poleg bližnjih predmetov ali objektov moč videti tudi zelo oddaljene objekte, na katerih se paralaksa tako rekoč ne zazna in služijo kot referenčna točka pri zlaganju slik - zelo oddaljeni točki se morata prekrivati, čeprav so mogoče tudi drugačne rešitve. Ima pa ročna metoda z enim fotoaparatom, ki ga zamikamo, veliko prednosti: zmeraj jo je možno uporabiti, slike so posnete na isti CCD senzor za zajemanje slik, optika je ista, je izjemno enostavna metoda. Največji pomankljivosti sta približna ocena zamika fotoaparata in rotacija, ki je posledica ročnega slikanja. Zanimivo je, da večina ljudi ne razume postopka 3D fotografije in misli, da je 3D fotografija zgolj posledica zamika ene slike. Tudi sama v šoli nisem spoznala logike, zakaj ljudje lahko svet zaznavamo globinsko. Škoda, da pri pouku ne obravnavamo te teme. Paralaksa se pri fiziki načeloma obravnava, pri tej snovi bi lahko povedali kaj več o globinskemu zaznavanju in 3D fotografiji. 3D fotografija mi je omogočila globlje razumevanje zaznavanja fizičnega sveta, ki pa močno vpliva tudi na duševnost, domišljijo in ustvarjalnost slehernega od nas. 3D fotografijo bi lahko izboljšala z uporabo profesionalne opreme, z dvema fotoaparatoma.
KAKO PA LJUDJE Z ENIM OČESOM ZAZNAJO PROSTORSKO GLOBINO?
Zaznajo jo s premikom glave in s tem sami povzročijo paralakso, to je enako moji metodi zamikanja enega fotoaparata. Torej tudi Kiklop vidi svet globinsko.
V nalogi sem pokazala, da je prostorska fotografija zgolj z enim fotoaparatom mogoča in z vajo tudi dovolj kvalitetna. Rezultate naloge si lahko ogledajo vsi radovedneži, hkrati pa jih lahko navdušijo, da se tudi sami spoprimejo s prostorsko fotografijo - ne bo jim žal. Rezultate moje naloge si lahko ogledate na moji spletni strani: http://www2.arnes.si/~lkkpcj1/fotografija3d/raz_nal3d.html Naloga mi je vzela veliko časa, a je bilo vredno, saj sem se ob delanju naloge zelo veliko naučila. V okviru razpoložljivega časa bom svet z veseljem še naprej slikala v 3D perspektivi. 3D fotografija bi lahko zelo kvalitetno popestrila mnoga področja našega življenja: turizem, šolstvo-izobraževanje, umetnost, arhitekturo, medicino, ...
Za konec pa še pismo gospoda Takashi Sekitanija, 3d mojstra iz Japonske:
»From: Takashi Sekitani sekitani @ stereoeye.jp
To: zorko.vicar @ guest.arnes.si
Subject: Re: Anaglyph Maker - wonderful tool
Date: Mon, 19 Mar 2007 23:09:53 +0900
Dear Zorko and Ana Vicar,
I am happy to hear that you enjoy my 3D website.
Research? I am interested in why you research 3D? :)
Anyway, Your JavaScript also works very well. Well done!
Thank you.
Best regards,
Takashi Sekitani
http://www.stereoeye.jp/
«
Avtorske pravice - komercialna uporaba gradiva je prepovedana, neprofitne predstavitve pa so dovoljene le z navedbo avtorice!
http://www.mojnet-si.net/Igre/3D_slike/3d-slike-valentinovo.html
http://www.mojnet-si.net/Igre/3D_slike/kako_gledamo_3d_slike.html
http://www.3dphoto.net/
http://www.3dphoto.net/world/europe/austriland/stefansdom.html
http://www.magiceye.com/enter.html
http://features.engadget.com/2004/08/24/how-to-tuesday-make-3-d-photos/
http://www.sungazer.net/3dsun.html
http://www.astro-nut.com/lunar-gibbous3D.html
http://www.callipygian.com/3D/holmes2ana.html
http://www.vision3d.com/3views.html
http://www.pulltime3d.com/
http://www.vision3d.com/optical/index.shtml#stereogram
http://www.mojmikro.si/?n=page&p=ufoto007
http://www.skytopia.com/project/illusion/illusion.html
http://mightyillusions.blogspot.com/2006/04/stereo-3d-animated-images.html
http://www.lohmueller.business.t-online.de/pov_anim/ani_3000d.htm
http://www2.arnes.si/~gljsentvid10/ocala1.html
http://antena.fe.uni-lj.si/~lso/gradivo/OOK/2p_ook.pdf
http://images.google.com/imgres?imgurl=http://herschel.jpl.nasa.gov/images/pellet_galaxy_anim.gif&imgrefurl=http://herschel.jpl.nasa.gov/farIRandSubmm.shtml&h=117&w=252&sz=69&hl=sl&start=10&tbnid=HNgbP2rooTXPOM:&tbnh=52&tbnw=111&prev=/images%3Fq%3Dexpanding%2Buniverse%2Banimation%26svnum%3D10%26hl%3Dsl%26lr%3D%26sa%3DN
http://antwrp.gsfc.nasa.gov/apod/
http://dogfeathers.com/java/hyprcube.html
http://www.stereoeye.jp/software/index_e.html
http://javor.pef.uni-lj.si/~or2006/Slapar_Klavdija/komplementarne_barve.htm
http://gimvic.org/predmeti/gradiva/oslikah/
--------------------------------------------------------
http://www.iol.ie/~geniet/3d/freeviewdeviation.htm#Stereo_base
http://home.vicnet.net.au/%7Evic3d/bases.html !!!!!!
http://home.vicnet.net.au/%7Evic3d/v3d.html
http://www.iol.ie/~geniet/3d/figure30.htm
http://www.herbig-3d.de/german/equ-norm_voll.htm#1
http://home.globalcrossing.net/%7Ezilch0/tools.htm
http://www.herbig-3d.de/german/variable_stereobasis.htm#g2 !!!
http://www.e-fotografija.com/artman/publish/printer_790.shtml
http://www.ed-mb.si/html/stereoskopija.html
|