


Uvod
Prispevek je bil prvotno namenjen predstavitvi
nekaterih dokaj preprostih tehnik snemanja
zvezdnih spektrov, oziroma mavričnih barv.
V mavrici (spektru) se skriva, poleg vizualne
lepote, neverjetno veliko informacij o sestavi
in življenju zvezd in ostalih vesoljskih objektov.
Čeprav so zvezde, glede na zemeljske dimenzije, zelo
daleč, so samo skromne pikice na nočnem
nebu, pa nam kljub temu preko, zaradi oddaljenosti, šibke svetlobe pošiljajo
neverjetne "osebne podatke", glej sliko pod
naslovom. Ob taki predstavitvi se zmeraj pojavi dilema,
kako globoko poseči v razlago pojavov.
Odločil sem se, da prispevek namenim navdušenim laikom,
in da ne bom prepričeval prepričanih,
zgolj z naštevanjem dejstev. Zato sem ubral dolgo,
ovinkasto in strokovno morebiti nevarno pot
poenostavljene razlage fenomenov, ki so lahko
za astronome in tudi za ostale bistveni pri dojemanju
dogajanja v svetu, ki ga živimo. Iz želje po
opisu pomembnih rezultatov spektrografskih vaj, ki jih
lahko praktično izvedejo na vsaki šoli, se bomo
po vrsti v grobem seznanili z valovanjem, Soncem,
uklonom, interferenco valovanja, ločljivostjo
teleskopov in ločljivostjo spektrografov na uklonsko
mrežico. Vmes pa bomo še sem in tja malo zašli
iz konteksta in komentirali to in ono, "nepotrebni"
komentarji bodo zapisani v sivem polju. Pot zna biti
občasno dolgočasna, a tu in tam se morebiti
dotika fenomenoloških temeljev našega dojemanja
in komuniciranja s svetom, del katerega smo s svojo radovednostjo
tudi mi sami. Kako pomemben del sveta in vesolja smo Ljudje?
Valovanje (1)
Valovanje ni samo vsem dobro znan pojav valov na in v vodi, ampak je valovanje tudi zvok,
elektromagnetni pojavi (radijski valovi, rentgenski žarki, gama žarki, svetloba …). Začuda
tudi delci, ki sestavljajo svet atomov in molekul, se obnašajo kot valovanje, odtod tudi
elektronski mikroskop in še bi lahko naštevali. Presenetljivo, tako rekoč vsa človeška
komunikacija in informacije kot take, temeljijo na pojavu valovanja
(govor, svetloba, radijski valovi …). Da se valovanja po izvoru in
tudi po obliki razlikujejo, bomo ponazorili z nekaj primeri. V splošnem
poznamo transverzalno in longitudinalno valovanje. Pri longitudinalnem
valovanju, recimo zvoku, nihajo delci (molekule zraka) vzdolž smeri
širjenja valovanja. V zraku se zato pojavijo zgoščenine in razredčine molekul,
kar pomeni tudi spremembo pritiska, kar zaznamo kot zvok. Pri napeti vzmeti lahko
en konec sunkovito vzdolžno podaljšamo ali skrajšamo in motnja, ki tako nastane,
se bo širila vzdolž vzmeti do drugega konca, če to delamo (nihamo) periodično,
dobimo spet longitudinalno valovanje. To je zdaj celo stoječe valovanje, kjer
brez težav opazimo razredčine in zgoščenine vzmetnih svitkov. Vzemite vsem dobro
znano igračko, vzmet iz trde raznobarvne plastike in poskusite, recimo z otrokom,
narediti nekaj vaj z napeto vzmetjo. Razdalja med dvema zgoščeninama ali razredčinama
je definirana kot valovna dolžina, označimo jo z grško črko lambda
(l).
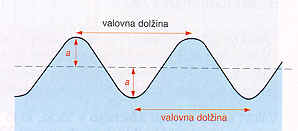
Pri transverzalnem mehaničnem valovanju pa, za razliko od longitudinalnega,
delci nihajo pravokotno na smer širjenja valovanja, recimo valovi na vodi,
strune na brenkalih itn. Spet si lahko pomagamo z napeto vzmetjo, ki jo
zdaj zanihamo prečno na dolžino. Brez težav opazimo, da vzmet valovi,
tako da nastajajo hribi in doline in razdalja med dvema hriboma ali
dolinama je kar valovna dolžina (l), glej sliko.


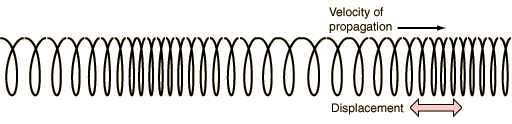


Zvok je tipičen primer transverzalnega valovanja. Kaj pa svetloba? Že zdaj je
potrebno poudariti, da je svetloba transverzalno valovanje, in da za razliko od
vseh ostalih valovanj (mehaničnih valovanj), za svoje širjenje ne potrebuje
nobenega sredstva. Za ponazoritev razlike si velja zapomniti, da zvok lahko
potuje samo po mediju, to je po snovi: plinu, kapljevini in trdni snovi; v
vakuumu ni moč širiti informacij neposredno z zvokom. Ker je večji del vesolja
napolnjen le z nekaj atomi na kubni meter, kar je vakuum, ki ga na Zemlji zlepa
ne dosežemo, vlada v vesolju zvočna tišina, ki pa jo zapolnjujejo mavrične barve
svetlobe. Eksperimenti kažejo, da je svetloba transverzalno valovanje električnega
in magnetnega polja, ki sta drug na drugega pravokotna. Magnetno in električno polje
ponazorimo s silnicami, glej sliko. Transverzalno valovanje lahko, za razliko od
longitudinalnega, polariziramo, kar pomeni, da recimo lahko struna ali pa električno
polje valovi samo v eni ravnini.
Single Slit Diffraction Intensity The Rayleigh Criterion -----------ločljivost http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
Single slit Circular aperture
Resolvance of GratingResolvance or "chromatic resolving power" for a device used to separate the wavelengths of light is defined as  The limit of resolution is determined by the Rayleigh criterion as applied to the diffraction maxima, i.e., two wavelengths are just resolved when the maximum of one lies at the first minimum of the other.
|
Index Grating concepts | |||||||
|
Go Back |
Examples of ResolvanceA standard benchmark for the resolvance of a grating or other spectroscopic instrument is the resolution of the sodium doublet. The two sodium "D-lines" are at 589.00 nm and 589.59 nm. Resolving them corresponds to resolvance  Another standard example is the resolution of the hydrogen and deuterium lines, often done with a Fabry-Perot Interferometer. The red lines of hydrogen and deuterium are at 656.3 nm and 656.1 nm, respectively. This requires a resolvance of 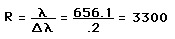 |
Index Grating concepts | ||
|
Go Back |
Resolvance of Grating
This gives the basic ideas, but the assumptions are shaky, so you might want a real derivation. |
Index Grating concepts | ||
|
Go Back |
Resolvance of Grating |
Index Grating concepts | ||
|
Go Back |















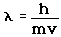
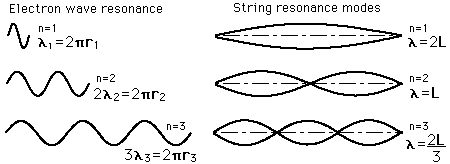
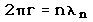
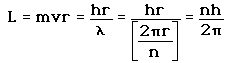
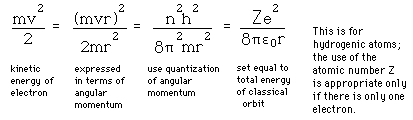
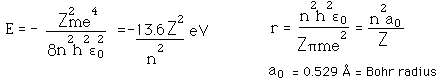



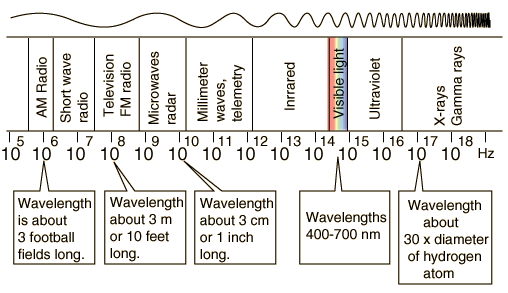
Svetloba, radijski signali, rentgenski žarki, gama žarki …, vsi ti fenomeni so pojavno elektromagnetni valovi, ki v vakuumu potujejo s hitrostjo c=300000km/s. To je tudi maksimalna možna hitrost sploh na Zemlji in v vesolju, vsaj v okviru današnjih meritev in tudi teorij. To pa pomeni, da je tudi širjenje informacij omejeno z limito 300000km/s. Glede na razdalje na Zemlji ta hitrost čisto zadostuje, kar lahko opazimo pri neposrednih televizijskih prenosih dogodkov in telefoniranju med celinami, kjer se zakasnitve dejansko ne opazijo. Vse kaj drugega bi bilo, če bi recimo nam najbližje večzvezdje Alfa Kentavra, oddaljeno 4,3 sv. let, imelo planetni sistem in na kakem izmed planetov razumna bitja in bi mi z njimi komunicirali. Čeprav je to poleg Sonca nam najbližja zvezda (v resnici večzvezdje) bi, ker je oddaljena 4,3 svetlobna leta, informacija potovala tja in nazaj skoraj 9 let. To pomeni, da če bi recimo v mali šoli pisali medzvezdno e-pošto prijatelju Kentaverčku, bi nam ta odgovor odposlal čez 4,3 leta in mi bi ga prejeli šele v osmem razredu. Elektromagnetno valovanje, del katerega je tudi svetloba, je sicer glede na dimenzije vesolja "počasno", a to ima tudi svojo prednost. Zakaj? Danes nam teleskop Hubble omogoča gledanje milijarde svetlobnih let daleč, torej tudi milijarde let nazaj v preteklost vesolja. Vidimo podobo objektov, predvsem galaksij, izpred milijard let, razkriva se nam "otroška" podoba vesolja. Lahko bi rekli, da imamo neposredni prenos iz preteklosti , "otroštva", kar s pridom izkoriščajo teoretiki za dopolnjevanje najbrž nikoli dokončnega modela in zgodovine vesolja. "Počasnost" in oddaljenost torej nimata samo slabih učinkov.
Še nekaj besed o valovni dolžini, frekvenci in hitrosti širjenja valovanja na primeru vzmeti. Kako dolga je valovna dolžina, je odvisno od časa nastajanja motnje in od hitrosti širjenja motnje. Nihajni čas ali perioda je čas to, ko vzmet pri longitudinalnem (vzdolžnem) vzbujanju potegnem recimo k sebi, nato popustimo, in jo spet potegnemo, da pride nazaj v prvotno lego. Pri transverzalnem (prečnem) vzbujanju pa je nihajni čas čas, ko recimo z roko vzmet dvignemo iz začetne lege navzgor, nato jo potisnemo navzdol in spet dvignemo v začetno lego. Ni si težko predstavljati, da v eni periodi ali nihajnem času, motnja naredi pot ene valovne dolžine. Hitrost (c) potovanja motnje je torej kar valovna dolžina (l) deljena s periodo, nihajnim časom to: c=l/to. Zadnji izraz bomo zapisali nekoliko drugače, in sicer bomo upoštevali pojem frekvence (oznaka n, izgovori se kot ni), ki nam pove, koliko motenj (nihajev) se je zgodilo v določenem času: n=št_nihajev/čas=en_nihaj/nihajni_čas=1/to. Enota za frekvenco je [1/s=Hz] ali Hertz. Hitrost bomo torej zapisali kot produkt valovne dolžine in frekvence: c=l(1/to)= ln. Ponovimo, hitrost (c), frekvenca (n) in valovna dolžina (l), so povezani med sabo v zvezo: c=ln. Zadnji izraz je izjemno pomemben in uporaben in velja za vsa valovanja.
Kako nastane elektromagnetno valovanje, oziroma svetloba?
(SL_4 Nastanek elektromagnetnega vala 22.22 v Principles of Physics, stran 512, ali Universe, stran 148)
Pojavov pri katerih nastane elektromagnetno valovanje je veliko, v principu pa je dovolj, da se zavedamo, da vsako pospešeno gibanje naelektrenih delcev povzroči, da ti delci oddajajo elektromagnetno valovanje. V vakuumu potujejo elektromagnetni valovi s hitrostjo c=300000km/s. Poglejmo nekatere primere nastanka e.m. valovanj. V radijskih oddajnikih oscilator harmonično (sinusno) pospešuje elektrone v anteni, ki seva elektromagnetno valovanje. Tudi termično gibanje nabitih delcev je zaradi trkov, molekularnih in atomskih sil pospešeno, tako da vsako telo, ki ima temperaturo višjo od nič kelvinov, oddaja elektromagnetno valovanje. Temperatura večja od nič kelvinov pomeni, da so atomski delci v gibanju, imajo kinetično energijo, oziroma da tisti, ki so vezani v snovi, nihajo. Ta fenomen je prvi pravilno izrazil Jožef Štefan z znamenitim zakonom o gostoti izsevanega energijskega toka (j) za črno telo: j=s*T4. s=5,669*10-8W/m2K4 je Štefanova konstanta, T temperatura v kelvinih, črno telo je definirano kot telo, ki absorbira elektromagneta valovanja vseh valovnih dolžin, hkrati pa jih lahko tudi emitira. Gibanje nabitih delcev skozi magnetno polje, ki pot delca, če hitrost ni vzporedna s poljem, ukrivi in s tem pospeši, tudi povzroči valovanje. Temu pojavu pravimo tudi sinhrotronsko sevanje. Na Zemlji generiramo tako sevanje v znanstvene potrebe v sinhrotronskih pospeševalnikih (pospeševalnik v Bazovici na meji s Slovenijo), na enak način pa tudi ukrivljamo curke elektronov v TV sprejemnikih. Kombinacij termičnih vplivov, vplivov elektromagnetnih polj in mnogih drugih dejavnikov je veliko in vsi ti pojavi se dogajajo tako v hladnem medzvezdnem prostoru, ki ga v glavnem napolnjuje vodik, v zvezdah, v jedrih galaksij ... Tudi na Zemlji smo naravnim virom elektromagnetnih valov dodali vrsto elektromagnetnih signalov, ki so produkt naše civilizacije (telekomunikacije, prenos visokih napetosti, industrijski, gospodinjski stroji in aparati, radarji, sateliti ...). Različnih virov elektromagnetnih valov je torej v vesolju in na Zemlji na pretek, samo zaznati jih je treba. Radijske valove detektiramo s paraboličnimi radijskimi teleskopi. Kako je s svetlobo? Del energije elektromagnetnih valov z valovnimi dolžinami med 400 nm in 700 nm zazna človeško oko kot svetlobo. Po domače, to je valovanje, ki človeku razsvetljuje življenje podnevi in tudi valovanje, ki ga zaznamo kot podobo nočnega zvezdnega neba. Zvezda Sonce je za nas najpomembnejša, saj nam Sončna svetloba poleg sveta v barvah daje neprimerno več. V "barvah", ki nam jih Sonce pošilja, Zemlja prejme 99% energije, brez katere naš planet ne bi bil obljuden, bil bi (oziroma najbrž bo, ko bo Sonce čez milijarde let ugasnilo) izjemno mrzla pusta krogla v temi vesolja. Zemlja prejme tudi do j=1400 J/sm2, to je 1400 J energije v eni sekundi na kvadratni meter. Joul (J) je enota za energijo, delo in toploto. Za lažjo predstavo, približno en Joul dela dovedemo jabolku, če ga poberemo s tal. Prejeta moč (1400W) na kvadratni meter v grobem ustreza moči električne grelne plošče, manjšega elektromotorja, moči plesalca pri dviganju soplesalke ... Potrebno je opozoriti, da vso oddano električno delo hidroelektrarn in termoelektrarn izvira iz energije Sončnih žarkov, ki omogočajo kroženje vode in rast živalskih in rastlinskih oblik življenja.
Ker so atomski delci ključni pri nastanku svetlobe, ponovimo zgradbo atoma? Najbrž se še vsi spomnimo, da je atomsko jedro zelo majhno, velikostni red 10-15m, sestavljeno iz protonov in ponavadi tudi iz nevtralnih nevtronov. Protonom smo dodelili, zaradi narave obnašanja, pozitiven naboj. Okrog jedra se nahajajo elektroni v tako imenovanih elektronskih oblakih. Število elektronov je enako kot število protonov v jedru. Elektronom smo, spet zaradi obnašanja, dodelili negativen naboj, protoni in elektroni se privlačijo, kar daje atomu stabilnost. Masa protona je mp=1,672*10-27kg, masa elektrona me=9,109*10-31kg, kar pomeni, da je elektron pravi palček, saj njegova masa znaša le 0,04% mase protona. Vsa masa atoma je torej v jedru, medtem ko pa velikost "paradoksno" določa elektronski oblak, saj je premer atoma 10-10m, kar je 100000 krat več od velikosti jedra. Iz povedanega sledi, da je naš materialni svet takorekoč prazen, si predstavljate, kako bi izgledal model atoma, če bi jedro atoma povečali na velikost okrogle lizike. Recimo, da je premer lizike 3cm, elektron naj predstavlja mravljica, katero lizika privlači in se zato živahno sprehaja okrog lizike. Razdalja do lizike bi bila v tem primeru kar 1,5 km in kljub izjemno majhni masi mravljice bi njen tir odločal o velikosti modela atoma, vmes pa je prostor takorekoč prazen. Dve jedri sta torej, v našem modelu atoma, najmanj 3km narazen. V primeru, da bi ljudje predstavljali atomska jedra, bi bil naš najbližji sosed več kot 100 km oddaljen. Mimogrede, če bi živeli na nevtronski zvezdi, kjer je gravitacija stisnila atomska jedra skupaj, bi se ljudje zmanjšali na mikronsko velikost mini palčkov.
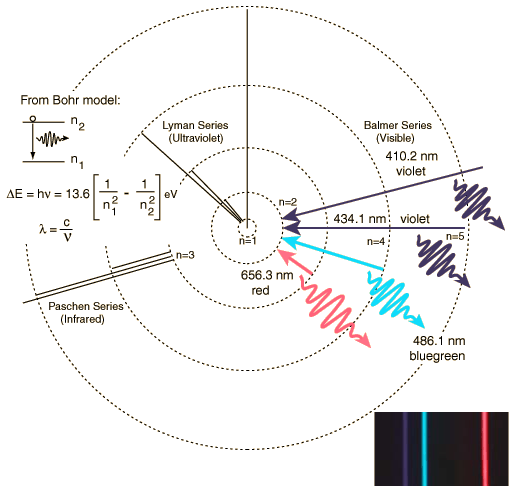
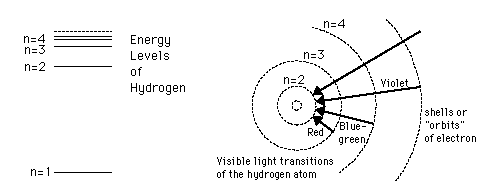
Poglejmo si podrobneje vodikov atom, saj je le ta najenostavnejši. Vodika je tudi največ v vesolju. Pametno zastavljeni eksperimenti so nas pripeljali do modela, da svetloba ostro določenih valovnih dolžin nastane pri točno določenih prehodih med diskretnimi energijskimi nivoji v atomih in molekulah oziroma ionih, glej sliko, primer vodikovega atoma.
(Sl_5. Model vodikovega atoma.)
To pa tudi pomeni, da lahko določen element, oziroma molekula,
pri danih pogojih, oddaja (prejema) svetlobo samo točno določenih
valovnih dolžin, ki pa se razlikuje od svetlobe drugih elementov.
Energija svetlobnega paketa, imenovanega foton, ima zato tudi
točno določene vrednosti, Wf=h*n=hc/l, h=6.6*10-34 Js je
Planckova konstanta. Podroben opis nastanka svetlobe zahteva
znanje predstavno in pojmovno kompleksne kvantne mehanike.
Kvantna mehanika poskuša razumeti dagajanja in pojave v svetu
atomov, ukvarja se z najmanjšimi gradniki sveta, medtem ko pa
se tako imenovana klasična mehanika Galileja, Hooka, Newtona
ukvarja z velikimi telesi in majhnimi hitostmi glede na hitrost
svetlobe. Za približno pojasnitev razlike med klasično in kvantno
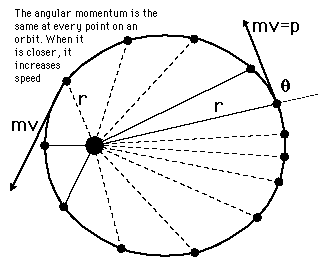
mehaniko si poglejmo primerjavo vodikovega atoma z Zemljo, okrog
katere kroži satelit. Okrog Zemlje mase M lahko kroži satelit mase
m s hitrostjo v, po kateri koli orbiti (na razdalji r od središča
planeta) in med orbitami (krožnicami) prehaja brez vsakih omejitev.
Energija satelita je seštevek kinetične (Wk=mv2/2) in potencialne
(Wp=-Gmm/r, G=6,6720*10-11m3/kgs2 je gravitacijska konstanta)
energije, W=Wk+Wp=mv2/2-GMm/r. Kako pa je z atomi? V modelu
klasične mehanike si recimo vodikov atom lahko predstavljamo
podobno kot planet in satelit. Okrog jedra (jedro je proton
mase mp=1,672*10-27kg) kroži elektron (masa me=9,109*10-31kg)
s hitrostjo v. Spet bi lahko energijo elektrona poenostavljeno
zapisali kot vsoto kinetične (Wek=mev2/2) in v tem primeru
električne potencialne energije (Wep=-epee/(4peor), ep in ee
sta naboja protona in elektrona, eo je influenčna konstanta).
Izkaže se, da taka poenostavljena slika v svetu atomov odpove.
Kroženje elektrona pomeni pospešeno gibanje negativnega delca.
Da je kroženje pospešeno gibanje, nas prepriča vožnja skozi ovinek,
ko čutimo neprijetno silo, ki nas potiska iz ovinka. Že prej pa smo
povedali, da pomeni pospešeno gibanje, recimo elektronov, tudi hkratno
oddajanje energije v obliki elektromagnetnih valov, kar pomeni, da bi
vodikov elektron izgubljal energijo in bi se bližal jedru in na koncu
združil z njim. To bi pa pomenilo, da bi se svet sesedel (zmanjšal)
za vrednost 10-5m. Nekaj podobnega se zgodi, ko iz masivne zvezde
pri eksploziji supernove nastane nevtronska zvezda, kar pa je posledica
sile gravitacije in ne energijskih izgub na račun elektromagnetnih valov.
Če bi človek pristal na nevtronski zvezdi ogromne gostote 1015kg/dm3
(gostote atomskega jedra ), kot smo že omenili, bi se v resnici sesedel,
zmanjšal na mikronsko vrednost. Ker se na Zemlji in Soncu to ne zgodi,
morajo veljati v svetu atomskih delcev prav posebni zakoni, ki jih skuša
opisati kvantna mehanika. Elektron se torej lahko nahaja le na točno
določenih "orbitah" in prehaja lahko le med njimi, recimo na višje ali
z višjih na nižje. Ker o gibanju elektrona in legi elektrona ne moremo
več govoriti s prispodobo krožečega satelita, raje rečemo, da se elektron
nahaja na točno določenih energijskih nivojih, oziroma v stanjih, ki so
diskretna. Po domače bi lahko rekli, da se svet atomov (elektronov) zmeraj
"premika po stopnicah", premika se diskretno, elektron skače iz ene
"stopnice" na drugo, kot otroci na domačem pragu. Svet velikih teles
pa ponavadi potuje po strmini, po hribu zvezno, kjer so dovoljne vse
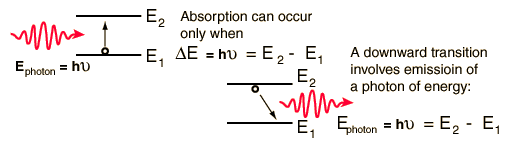
lege in vsi koraki. Prehod elektrona na višji energijski nivo lahko
sproži trk z drugim atomskim delcem ali absorbcija svetlobe (absorbira
se svetlobni paket imenovan foton) točno določene energijske vrednosti,
ki ustreza prehodu na višji nivo (otrok stopi na višjo stopnico).
Ko pa elektron preide z višjega (W1) na nižji energijski nivo (W2),
pa odda elektromagnetni energijski paket (foton), po domače kar svetlobo,
in to spet s točno določeno energijsko vrednostjo (W2-W1=Wf=hn=hc/l)
oziroma valovno dolžino. Primerjava z otrokom, otrok stopi na nižjo
stopnico. Energija fotona, ki je elektron dvignila na višji energijski
nivo, je enaka energiji oddanega fotona (svetlobe), če elektron spet
preide na isti začetni višji energijski nivo. Tudi valovni dolžini
sta enaki, saj velja povezava: hc/l =W2-W1, oziroma l=hc/(W2-W1).
Sedaj je mogoče že lažje razumemo, zakaj različni plini oz. atomi
in molekule, oddajajo (sevajo) svetlobo različnih barv. Za vodik se
s pomočjo Balmerjeve enačbe da izračunati valovne dolžine izsevane
svetlobe. Enačba se glasi , v kateri je n2=1,2,3..
(SL_ Za Dopplerja podaj iz Universe sliko 5-19 stran 96)
(SL_ Za ponazoritev spektra uporabi vodikov spekter iz Universe
6-12 stran 115)
(10000 rež na cm)
(SL_ Zanimiv spektrograf oz. spektroskop na prizmo iz Astronomy, stran 68.)
Sevanje Sonca in nastanek absorbcijskih črt
Poglejmo, zakaj Sonce seva tolikšno energijo v medzvezdni prostor in to s
konstantnim energijskim tokom 3,86*1026W, že 5 milijard let. Načeloma veljajo
enaki principi tudi za ostale zvezde. Sonce je nam najbližja zvezda mase
1,99*1030kg, polmera 6,96*105km in povprečne gostote 1,4kg/dm3, povprečna
razdalja do Zemlje je 150*106km. Za primerjavo, masa Zemlje je 5,98*1024kg,
polmer 6370km, povprečna gostota 5,5kg/dm3. Sonce je razbeljena plinska
krogla, ki črpa energijo iz jedra, kjer sta temperatura (@16*106K) in tlak
(@2,5*1016Pa), dovolj visoka, da se vodik zliva v helij. Za zlivanje jeder
je potrebna sila, ki je večja o odbojne sile med protoni. To pa pomeni,
da se morata jedri približati drug drugemu do razdalje, ko postane močna
jedrska sila večja od elektrostatske odbojne sile med protoni. To pa se v
naravi lahko zgodi samo v sredicah zvezd, kjer je gostota atomskih jeder,
predvsem pa njihova hitrost, ki je sorazmerna s korenom temperature, dovolj
velika. Tako stanje snovi imenujemo plazma, to je izjemno vroč plin sestavljen
iz elektronov in golih jeder. Če stehtamo maso vodikovih jeder pred zlitjem in
helijevega na koncu, bomo videli, da je helijevo jedro nekoliko lažje. To pomeni,
da se pri tej reakciji, rečemo ji tudi termonuklearna reakcija, pretvori del mase
(0,7%) v energijo, katere del gre v gama (g) elektromagnetno valovanje. Energija,
ki se sprosti, se izračuna iz Einsteinove zveze (W=Dm*c2=26,7Mev, Dm je razlika
mas, c je hitrost svetlobe, eV je 1,6*10-19 J). To je torej glavni vir izsevane
energije, ki hkrati drži temperaturo in tlak milijarde let konstanten in tako
preprečuje gravitaciji, da bi zvezdo stisnila. Verigo reakcij, ki pripelje
vodikove atome (ione) do helija, ki ima 2 elektrona, v jedru pa 2 protona in
2 nevtrona ( ), lahko zapišemo na sledeč način:
Štirje vodikovi atomi ( ) se torej zlijejo v helijev atom ( ), pri čemer se
sprostita še dva pozitrona (pozitivna elektrona ) in elektronska nevtrina ( ).
Seveda se veriga reakcij nadaljuje v berilij, litij, bor, če temperatura v zvezdi
naraste na 108K se vname helij in izgoreva v ogljik in kisik, dušik, pri še višjih
temperaturah se z zlivanjem jeder pojavljajo zmeraj težji elementi in izotopi: neon,
silicij ... Vse je torej odvisno od mase zvezde, saj le ta pogojuje temperaturo
zvezdne sredice, po domače, masivnejše zvezde same sebe, zaradi lastne teže, močneje
stiskajo in jim je zato bolj vroče. Podobna primerjava bi se dala potegniti tudi med
ljudmi, kjer pa težave "močnejših" ljudi ne izvirajo zgoj iz gravitacije.
(SL_7 Vujnovič stran 84, slika 4.6)
Sonce izseva v eni sekundi 3,86*1026J energije, izračunajte iz Einsteinove zveze
(energija=Dm*c2), za koliko se zaradi izseva zmanjša masa Sonca v eni sekundi.
Materija torej ni večna, kot to še mnogi danes praznoverno trdijo, je le ena
izmed oblik energije. Prenosi sproščene energije iz jedra na površje zvezde so
zelo kompleksni in prenos traja lahko tudi 10 milijonov let, kar pomeni, da nas
danes grejejo žarki, ki so se načeloma sprostili, ko še moderni človek ni bil del
življenja na Zemlji. Ker so temperature v središču Sonca visoke, so tam najmočneje
zastopani rentgenski žarki, na površini pa vidni del elektromagnetnega valovanja,
svetloba.
(SL_8 M. Astrophysics stran 328/slika 11.1 A)
Sonce je staro približno 5 milijard let in še zmeraj je v njegovi sestavi
najmočneje zastopan vodik (okrog 75%), helija je okrog 24%, ostalih elementov
pa 1%. Seveda je v jedru nekaj manj vodika na račun helija, ki v jedru tudi
nastaja. Temperatura površja Sonca (fotosfere) je okrog 5780K. Ker se vroč
plin zaradi vzgona dviga in s tem ohlaja in zato spet spušča, nastanejo na
Socu konvektivne celice, imenovane granule velikosti 1000km in več, ki pa
imajo na robu nekoliko nižjo temperaturo. Na Soncu so tudi večje konvektivne
celice supergranule, velike so tudi do 30000km. Poleg granul se zaradi magnetnih
polj pojavijo nehomogenosti v porazdelitvi temperatur, kar se odraža v fenomenu
Sončevih peg, kjer lahko temperatura pade tudi na 3500K. Kako globoko vidimo v
Sonce, razbeljeno plinsko kroglo? Sloj do katerega vidimo imenujemo fotosfera,
to je spodnja plast atmosfere in hkrati meja za določanje velikosti Sonca.
Fotosfera je debela do 500km, večino svetlobe iz fotosfere gre v vesolje.
Sledita kromosfera (debelina 10000km) in korona, ki se razteza v medplanetarni
prostor. Zadnji dve plasti lahko zelo enostavno opazujemo ob popolnih Sončnih
mrkih, ne pozabite na mrk 11. avgusta letos.
(SL_9 M. Astrophysics stran 396/slika =)
V spektru Sončne svetlobe imamo dva pojava. Fotosfera seva zvezni spekter vseh
valovnih dolžin, saj je temperatura tako visoka, da so atomi ionizirani in ni
moč pričakovati črtastega spektra. Od začetka kromosfere do višine 1500km pade
temperatura na 4000K in zaradi tega se tukaj že pojavijo absorbcijske spektralne
črte atmosferskih elementov. V teh slojih so namreč že tudi zastopani neionizirani
atomi vodika, helija, železa, magnezija, kalcija ... nad 60 elementov. Temperatura
v višjih slojih atmosfere spet raste, vendar je gostota zelo majhna, saj pade od
gostote fotosfere, nekaj sto milijonink gostote zraka (velikostni red 1018atomov/cm3)
le na 109atomov/cm3, tako da svetloba emitirana v teh plasteh ne vpliva bistveno na
spekter. Joseph Fraunhofer je leta 1814 s spektroskopom na prizmo odkril okrog 600
spektralnih črt, danes jih poznamo milijon. Če ponovimo, v sicer zveznem spektru z
vsemi valovnimi dolžinami, se pojavijo temnejše lise, ker pri določenih valovnih
dolžinah gostota svetlobe pade, saj se le ta absorbira v hladnejših plasteh atmosfere.
Kateri fotoni se bodo absorbirali, pa določajo gradniki atmosfere, saj vsak element
lahko absorbira le točno določene valovne dolžine. Atmosfera sicer spet emitira
absorbirano svetlobo, vendar v vse smeri, tako da v smer opazovnja vrne le del
"ukradene" svetlobe. Tako torej nastanejo Fraunhoferjeve absorbcijske spektralne
črte, ki nam elegantno pomagajo določiti sestavo zvezdine atmosfere. Velikokrat
nam preproste računalniške animacije zelo pomagajo pri ustvarjanju celostne podobe
kakega pojava, prav nastanek emisijskih in absorbcijskih spektralnih črt je lepo
ponazoril Peter Mihor z animacijo na URL naslovu:
http://www2.arnes.si/~ssdpmiho/spekter.html, ali
http://www.kvarkadabra.net/vesolje/animacije/spekter.htm
(SL_10 Vujnovič 2, stran 24, kaj podobnega neriši, ali vzami iz Astronomy
ali iz universe).
Da sevajo zunanje plasti atmosfere izrazito prav v valovnih dolžinah, ki so
slabo zastopane v spektru zvezde, se bomo lahko 11. avgusta letos prepričali
ob popolnem Sončnem mrku. Ko Luna prekrije Sonce, se v spektru Sonca pojavijo
le črte zunanjih plasti atmosfere, saj Luna zastira svetlobo s fotosfere, glej
spodnjo sliko iz Sky&Telescope. Zgolj z uklonsko mrežico pred objektivom (reža
zdaj ni potrebna, saj je atmosferski lok dovolj tanek), boste lahko 11. avgusta
prav vi posneli emisijski spekter Sončne atmosfere. Da bo slika uspela (izbira
mrežice, objektiva, filma, stojala), naredite nekaj testnih posnetkov Sonca že
prej, pazite na oči. Da posnamete ta izjemni efekt imate na voljo le nekaj sekund.
(SL_11 dostavi Sky&Telescope stran 109, marc 1995).
Seveda je potrebno omeniti, da se zastopanost, izrazitost, širina absorbcijskih
črt … od zvezde do zvezde spreminjajo, saj se zvezde med sabo razlikujejo po
sestavi in temperaturi, zato tudi zvezde delimo v spektralne razrede. Soncu
podobne zvezde spadajo v spektralni razred G, glej sliko (iz astronomy ali
universe). Že po barvi zvezde lahko sklepamo na temperaturo zvezde, oziroma
na spektralni tip. Valovna dolžino pri kateri je gostota svetlobnega toka
največja, je odvisna od temperature. Sonce nam prinese največ energije z
rumeno in zeleno svetlobo valovnih dolžin blizu 500nm. Zdaj tudi razumemo,
zakaj Sonce vidimo v rumeni barvi, čeprav nam že mavrica odkrije, da je v
svetlobi Sonca zastopanih mnoštvo barv (valovnih dolžin). Zelo uporabna je
Wienova zveza med temperaturo površine zvezde in valovno dolžino, kjer je
gostota elektromagnetnega valovanja najvišja l*T=0,002898mK. Lahko preverite
veljavnost zakona za Sonce. Ker je temperatura obratno sorazmerna z valovno
dolžino maksimuma spektra (T=(0,002898mK)/l), lahko sklepamo, da so modre
zvezde bolj vroče od zelenih, zelene od rumenih, oranžne od rdečih …, saj
z naraščanjem valovne dolžine od modre do rdeče vrednost kvocienta
(T=(0,002898mK)/l) pada. In v resnici je naša približna očesna
spektroskopija dovolj dobra za oceno temperature zvezd. Vse zvezde
s temperaturo okrog 6000K so enake barve, enakega tipa, glej sliko
porazdelitve spektra elektromagnetnega valovanja črnega telesa.
{PODAJ spektralne razrede, barve in TEMPERATURE}
{SL_12a, podaj spekter črnega telesa in spektralne razrede zvezd s
primeri ???}.
Na širino črt, neostrost pri določanju vrednosti valovne dolžine, v
glavnem vplivajo trki med atomi in hitrost atomov, ki je povezana s
temperaturo. Zaradi različnih smeri gibanja atomov se spektralne črte
zaradi Dopplerjevega pojava razširijo. Intenziteta spektralne črte je
porazdeljena po zvonasti krivulji. Za širino črte Dl1/2 vzamemo kar
debelino na polovici krivulje (glej sliko). Ker je kinetična energija
atomov in molekul odvisna od temperature, bo hitrost (v) sorazmerna s
korenom temperature in obratno sorazmerna s korenom mase delca (mo).
Sprememba valovne dolžine svetlobe zaradi gibanja delcev (Dopplerjev
pojav) je Dl=l*v/c. Širina črt Dl1/2 je torej, odvisna od konst*l .
Pri razširitvi zaradi trkov je potrebno malo več truda, vendar se
izkaže, da so tudi v tem primeru pomembni temperatura, masa delca
in še številčna gostota delcev ter dimenzije delcev. Tudi če odštejemo
oba vpliva na razširitev črt, ima valovna dolžina neko naravno razširitev,
edoločenost, ki je v grobem odvisna od časa vztrajanja atoma v določenem
energijskem stanju. Skratka, zašli smo že v področje nedoločenosti merjenih
količin, ki je eno izmed temeljev kvantne mehanike in je za nas v
tem kontekstu prezahtevno.
(SL_12b, glej sliko iz universe ali astronomy, za Dopplerja podaj
iz Universe sliko 5-19 stran 96).
Vsekakor o širini črt odloča temperatura, oziroma kinetična energija
delcev. Širino črt za nekatere elemente na Soncu kaže tabela. Izrazito
širino opazimo pri atomih kalcija in tudi vodika in natrija. Na našem
posnetku spektra so te črte v resnici zelo široke. Poglejmo zakaj je
kalcijeva črta tako intezivno zastopana? Atom kalcija ima 20 nevtronov
in 20 protonov, torej tudi 20 elektronov. Kalcij je v glavnem v atmosferi
že enkrat ioniziran (Ca+), kar pomeni, da ima še zmeraj preostale elektrone
vezane v elektronski oblak. Primerjajmo kalcij z vodikom glede intenzitete
absorbcije. Vodikova absorbcijska črta alfa (656,28 nm) je posledica prehoda
med drugim in tretjim energijskim nivojem elektrona. Da elektron preide
na drugi energijski nivo rabi energijo 10,2eV, za ionizacijo kalcija
pa rabimo manj energije, 6,11eV. Praktično je ves kalcij ioniziran (Ca+),
le eden med 900 atomi je nevtralen, medtem ko pa je samo eden izmed 200
milijonov vodikovih atomov v vzbujenem stanju n=2. Vodika je sicer res
500 000 krat več kot kalcija, a na 400 ionov kalcija
(200 milijonov/500000=400) pride samo en vodikov atom
v stanju n=2. Kljub ionizaciji pa ioni kalcija (vezani
elektroni) lahko še zmeraj prehajajo na višje energijske
nivoje in to tudi z absorbcijo fotonov valovnih dolžin
lH=393,36nm in lK=396,84nm, ki sta tako izrazito zastopani v
spektru. To je tudi razlog, da sta absorbcijski črti H in K
bolj izraženi kot recimo alfa črta vodika, čeprav je vodika
500000 krat več kot kalcija. Tako razmerje je seveda pogojeno
s sestavo in temperaturo atmosfere Sonca. Kalcij bo ukradel
svetlobi fotosfere več njemu značilnih fotonov kot vodik,
zmagal je torej "šibkejši", oziroma manj številčen element.
Na našem posnetku se izrazitost H in K črt kalcija lepo vidi.
(SL_13, izsek iz našega spektra, predvsem črti H in K)
(SL_14 Modern Astrophysics, stran 240 graf 8.9. mogoče samo CaII
in H ali z drugo barvo).
(SL_15 Glej še vujnovič 43 (2.17 slika) in 46 slika 2,23)
Najizrazitejše Fraunhoferjeve absorbcijske črte.
Ponovimo, svetloba je, tako kot radijski, rentgenski valovi, gama žarki …,
transverzalno valovanje električnega in magnetnega polja, ki sta drug na
drugega pravokotna. Magnetno in električno polje ponazorimo s silnicami,
glej sliko.
Elektromagnetne valove valovnih dolžin od 400nm do 700nm imenujemo svetloba,
saj jih naše oko in možgani zaznajo kot barve.
Še nekaj besed o radijskih, rentgenskih in gama valovih.
Kako nastanejo nadvse uporabni radijski valovi? Tudi radijski valovi nastanejo
pri prehodih med diskretnimi energijskimi nivoji v atomih in molekulah, vendar
je mehanizmov še več, saj vsako pospešeno gibanje naelektrenih delcev povzroči,
da ti delci oddajajo elektromagnetno valovanje. V radijskih oddajnikih oscilator
harmonično pospešuje elektrone v anteni. Vzrok za nastanek radijskih valov je tudi
termično gibanje nabitih delcev, potem gibanje nabitih delcev skozi magnetno polje,
ki pot delca, če hitrost ni vzporedna s poljem, ukrivi in s tem pospeši. Temu pojavu
pravimo tudi sinhrotronsko sevanje. Na Zemlji generiramo tako sevanje v znanstvene
potrebe v sinhrotronskih pospeševalnikih, na enak način pa tudi ukrivljamo curke
elektronov v TV sprejemnikih. Kombinacij termičnih vplivov, vplivov elektromagnetnih
polj in mnogih drugih dejavnikov je veliko in vsi ti pojavi se dogajajo tako v
hladnem medzvezdnem prostoru, ki ga v glavnem napolnjuje vodik, v zvezdah, v
jedrih galaksij ... Radijskih virov je torej v vesolju na pretek, samo zaznati
jih je treba. Del energije elektromagnetnih valov prestrežemo z antenami
(radijskimi teleskopi), ki so ponavadi parabolične in čim večje, da zberejo
več energije in imajo večjo kotno ločljivost.
Rentgenski žarki so ponavadi posledica zavornega sevanja visokoenergijskih
elektronov, gama žarki pa ponavadi nastanejo pri termonuklearnih reakcijah.
Oboji žarki so izjemno visokih frekvenc in kratkih valovnih dolžin, kar pomeni,
da nosijo s sabo veliko energije in so zelo prodorni. Obe lastnosti sta zelo
nevarni za življenje na zemlji, čeprav so paradoksno, lahko prav ti visokoenergijski
žarki v zmernih dozah, preko mutacij pripeljali do človeka.
Konec uklon12.doc
{sledi zacetek uklon22.doc
Uklon in interferenca valovanja (2)
}
Uklon1.doc (uklon1.doc=uklon12.doc + uklon22.doc)
Konec uklon22.doc
{ostaneka uklon12.doc
teleskopi), ki so ponavadi parabolične in čim večje, da zberejo več energije
in imajo večjo kotno ločljivost.
}
Uklon in interferenca valovanja (2)
Ker si ljudje lažje predstavljamo valove kot hribe in doline, si bomo s pomočjo
valovanja na vodi na hitro pogledali dve lastnosti valovanja, ki sta nujno potrebni
za razumevanje spektrografije in ločljivosti optičnih inštrumentov. Tisto kar nam je
vsem znano, je dejstvo, da se valovanje, recimo zvok, tudi širi za oviro, se ukloni.
Zvok, sicer oslabljen, pa vendarle, se širi za vogal hiše, kar smo kdaj tudi kot
otroci skriti za vogalom s pridom izkoristili za prisluškovanje važnim pogovorom
odraslih. Iz slike se lepo vidi, da se valovi, ki so zadeli ob oviro, uklonijo
tudi za oviro.
(SL_ slika ovire in valov, 1x)
Kaj pa se zgodi, če pravokotno na smer širjenja valovanja postavimo režo,
recimo dve dolgi oviri in med njima spreminjamo razdaljo. Sliki spodaj sta
zelo poučni in pomembni. Pri levi sliki je razdalja med ovirama nekaj valovnih
dolžin. Jasno je, da pride do uklona, a oster pogled bo opazil še več, za režo
dobimo poleg uklona še smeri z višjimi valovi (večjo amplitudo) in smeri z nižjimi
valovi. Primer si dobro zapomnimo, k njemu se bomo še vrnili. Desna slika pa
prikazuje uklon na ozki reži, širina je manjša od valovne dolžine. Na drugi
strani dobimo takorekoč polkrožne valove, podobno, kot da bi v vodo metali
kamenčke, ki povzročijo valove v obliki koncentričnih krogov, pravimo da imamo
točkasti izvor valov.
(SL_ 2x slika, Uklon na reži iz Principle of Phisycs na strani 583-fig.25.1,
leva slika in tudi ostale, glej še do strani 602, glej še uklon iz svio1
strani 46 in 47)
Vsekakor radovedneže zanima, kaj se zgodi z valovanjem, če sestavim dva ali
več točkastih izvorov valovanja. Spodnja leva slika je nadvse zanimiva,
poskušajmo si razjasniti pojav, zakaj je valovanje v določenih smereh
ojačano, v nekaterih pa oslabljeno. Ali o smereh ojačitev (oslabitev)
odloča valovna dolžina in razdalja med izvoroma? To odvisnost lahko brez
težav potrdimo s sredinsko in desno sliko. Pa poglejmo ali lahko to
odvisnost tudi matematično zapišemo? Pojav, ko se več valovanj sreča,
posledice so ojačitve in oslabitve valov, imenujemo interferenca.
Premislek, ki ga bomo naredili, je eden pomembnejših v fiziki in v
znanosti nasploh in brez njega si težko predstavljamo razvoj mnogih
naravoslovnih znanosti do stopenj, ki jih danes poznamo.
(SL_ sliki a, b, c. Uklon in interferenca na vodni gladini OBVEZNO)
Za izhodišče naj bosta spodnji sliki, ki enostavno peljeta k našemu cilju.
Za poenostavitev bomo seveda obravnavali dva točkasta izvora. Kaj lahko
razberemo? Če se srečata hriba in dolini dveh valovanj (leva slika),
tako da sovpadata, sta valovanji v fazi in se seštejeta, potem dobimo
ojačano valovanje, valovi (amplitude) so višji. Če se pa srečata hrib
in dolina dveh valovanj (desna slika), pravimo, da sta valovanji v
nasprotni fazi, potem se valova odštejeta (izničita) in valovanje na
tem mestu popolnoma oslabi. No sedaj pa moramo ta dva skrajna primera
še prenesti v matematični zapis. (SL sliki 1,2)
Izberimo si poljubno točko T dovolj daleč vstran od dveh točkastih
izvorov in zapišimo s pomočjo slike, kdaj pride do ojačitev oziroma
oslabitev v dani točki in tudi smeri glede na simetralo obeh izvorov.
Izvora oddajata sočasno (sinhrono) hribe in doline, sta v časovni fazi.
Pomoč naj bo spodnja slika.
(SL_ ,Interferenca dveh valov, ojačitev in oslabitev. Interferenca dveh
točkastih izvirov)
Valovanje naredi od izvora 1 do točke T pot r1, od izvora 2 pa pot r2.
Če se bosta v točki T srečala hriba oziroma dolini, se pojavi ojačitev valov.
Premislimo, to se zgodi, če je razlika poti r1 in r2 cel mnogokratnik valovne
dolžine. Pa zapišimo ta stavek še v matematični simboliki:
Dr=r2-r1=N*l. Število N ima lahko vrednosti: 0, ±1, ±2, ±3, … in določa tudi
red interference.
Iz geometrije na sliki se da razbrati, da je v primeru, če je razdalja a
nekajkrat večja od razdalje d med izvoroma, trikotnik z ogljišči (s,z,T)
zelo podoben trikotniku z ogljišči (1,2,3). To pa pomeni, da je razmerje
Dr/d, enako kot x/l, l je po pitagoru kar . Iz praktičnih razlogov bomo
to razmerje izrazili s sinusno funkcijo, iz definicije katere sledi, da je
sin(j)=x/l. Na koncu poenostavimo izraz za ojačitev, in
sicer: Dr/d=(N*l)/d=sin(j), oziroma:
D*sin(j)=N*l
{na sliki naj bodo ojačitve podane še s formulo pri vsaki smeri ojačanja oz.
oslabitev, zaradi nazornosti}
To pa je povezava, ki smo jo iskali. Za oslabitev velja podoben razmislek, na
hitro poiščimo povezavo. Da se srečata hrib valovanja 1 in dolina valovanja 2,
morata biti poti zamaknjeni za polovico valovne dolžine ali pravilneje za lihi
mnogokratnik polovice valovne dolžine l/2 (liha števila dobimo z enačbo 2N+1,
ostanek deljenja lihega števila z dva je zmeraj 1, naštejmo nekaj lihih števil
1, 3, 5, 7, …), Velja:
D*sin(j)=(2N+1)*(l/2)
Vsekakor velja, da je razlika poti na simetrali obeh izvorov enaka nič,
to je takoimenovani ničelni red (N=0), kar pomeni, da na simetrali dobimo
ojačano valovanje.
Razmislek o nastanku valovnih oslabitev in ojačitev, krajše interferenci,
ki smo ga naredili na vodni površini, lahko brez težav razširimo na ostala valovanja.
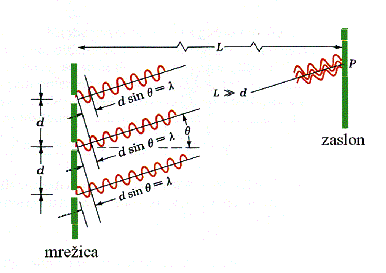
Uklonska mrežica (recimo nekaj sto vgraviranih vzporednih sledi, oziroma
raz na mm v steklu) svetlobo ukloni in pojav interference se da enostavno
opazovati na zaslonu, kjer se pojavijo ojačitve in oslabitve. Če je svetloba
sestavljena iz večih valovnih dolžin, se to na zaslonu odraža kot mavrica.
Seveda za določanje smeri ojačitev valovanja velja že izpeljana zveza (d*sin(j)=n*l).
Medmrežna razdalja d je v našem primeru znašala d=(1/530)mm, saj smo uporabili
mrežico z gostoto 530 raz na mm.
Ločljivost teleskopa in spektrografa (3)
Že v primeru prehajanja vodnih valov skozi režo, široko nekaj valovnih
dolžin, smo opazili očiten uklon valovanja in hkrati tudi smeri z ojačitvami,
oziroma oslabitvami valov. Enako se dogaja na vhodnih odprtinah teleskopov,
saj vhodna odprtina ukloni svetlobo. Takoj lahko ugotovimo, da so teleskopi
z majhnimi vhodnimi odprtinami, amaterski teleskopi, zaradi močnejšega uklona,
po ločljivosti slabši od svojih bratov velikanov z metrskimi premeri,
ki pa amaterske palčke že tako in tako prekašajo v svetlobni zmogljivosti.
Kaj sploh vidimo v teleskopu oziroma, kaj nam kaže teleskop? Če opazujemo
zvezdno nebo, se nam zdi, da vidimo zvezdice kot točkaste raznobarvne
lesketajoče se pikice. V resnici pa opazujemo interferenčne ojačitve
(maksimume) ničelnega reda, za kar je seveda kriv uklon na vhodni odprtini
teleskopa. Ojačitvi sledi krog z oslabitvijo in nato spet krog z ojačitvijo.
Slika je dejansko sestavljena iz koncentričnih krogov (zaradi krožne vhodne
odprtine), le da imajo interferenčni krogi višjega reda majhno gostoto
svetlobnega toka in dejansko vidimo samo ničelni red (glej sliki spodaj,
zvonasta funkcija sv. toka glede na kot j in še pogled od zgoraj,
koncentrični krogi)
{SL_ , poišči v knjigah slike, M. Astrophysics}.
Kako bi bolj natančno definirali ločljivost? Vsekakor si želimo, da s
teleskopom ločimo kar se da fine podrobnosti, recimo komponenti dvojne
zvezde V Velikega medveda, to je Mizar sestavljen iz zvezd A in B, ki
sta narazen 14 ločnih sekund. 14 ločnih sekund je zorni kot, oziroma kot,
ki bi ga oklepali premici, ki bi povezovali naše oko in obe zvezdi. Iščemo
torej minimalni kot jo, definiramo ga kot ločljivost, ki nam, preprosto
povedano, določa koliko sta lahko še skupaj dve točki (zvezdi), da ju še
med sabo ločimo in se nam torej ne zlijeta v eno točko, zvezdo, svetilo ...
Rešitev bomo poiskali v interferenčnem opisu uklonjenega valovanja na vhodni
odprtini.
{SL_ ,Iz Vujnoviča 2, stran 5 in 6. }
Pomagajmo s skicami. Uklonjeni valovi vzdolž reže se med sabo prav tako
ojačujejo in slabijo. Vsekakor bodo oslabeli valovi v smereh, v katerih
je razlika poti od 0 na enem koncu reže, pa do l na drugem koncu reže.
Razlog je v tem (glej spodnjo sliko in trikotnik abc), da se poti valov
na eni polovici reže (kjer je razlika poti od 0 do l/2) razlikujejo za l/2
od poti valovanj v drugi polovici reže (kjer je razlika poti od l do l/2).
Zaradi tega se valovi iz prve in druge polovice reže odštevajo (izničijo),
saj ima vsak val v eni polovici par v drugi polovici reže, razliki poti,
kot že vemo, pa sta za vsak par l/2. Sinus kota j1 pod katerim pride do
prve oslabitve je sin(j1)=l/D, glej sliko in trikotnik abc. Do naslednje
izrazite oslabitve pride pod kotom, ko je razlika poti 2l, v tem primeru
se režo razdeli na 4 enake dele in razmislek je za sosednja razdelka enak
kot pri prvem minimumu, ko smo režo razdelili na dva dela. Druga oslabitev
se torej pojavi pod kotom sin(j2)=2l/D. Iz povedanega sledi, da izraz za
določanje smeri oslabitev lahko izrazimo s splošno
formulo sin(j)=±(N+1)l/D, N je 0, 1 ,2, 3 ... V smeri režine
simetrale dobimo zmeraj ojačitev, enačba za določanje ostalih smeri
ojačitev je sin(j)=±(2N+1)l/2D, N je 1, 2, 3 ..., verjemite ali pa sami
premislite na enak način, kot smo za oslabitve. Sedaj lažje razumemo zakaj
se valovanje na reži ožji od valovne dolžine ukloni po celotnem prostoru
oziroma površini (polju). Ker je sinus kota prve oslabitve sin(j1)=l/D,
se bo kot oslabitve večal, bližal 90o, če bomo zmanjševali širino reže D.
Kvocient ±l/D je v primeru, če je l=D enak ±1, kar ustreza kotu ±90o, ničelni
ojačani red uklonjenega valovanja pokrije torej celotno izhodno področje.
Koncentrični (pol)krogi, ki predstavljajo valove, so enaki kot pri točkastem
izviru. Dogajanje pri uklonu ni enostavno, saj pri manjši širini reže od valovne
dolžine naraste kvocient nad 1, kar pa po definiciji sinusa ni možno in enačba odpove.
To pa za nas ni tako pomemben problem, saj je naš razmislek veljal za reže, ki so širše
od valovne dolžine. Pri reži ožji od valovne dolžine razlika poti iz dveh poljubnih
točk reže nikoli ne more biti enaka valovni dolžini, kar pomeni, da do oslabitev
sploh ne pride in je uklon sestavljen samo iz ojačitve.
Za morebitne bolj učene in zahtevne bralce je potrebno povedati, da
je v resnici naš razmislek groba poenostavitev Fraunhoferjevih in
Fresenelovih računov. Vrnimo se torej k naši reži in ločljivosti.
Ničelni red (N=0) nam da ojačano valovanje, sinus kota prve oslabitve
pa je iz pogoja (D/2)sin(j1)=l/2, kar sin(j1)=l/D. Ker je kot j1 majhen,
velja j1(v radianih)=l/D. Kako nam ta dva podatka lahko koristita?
Premislimo, če sta zvezdi tako blizu skupaj, da je zorni kot manjši od
smeri interfernčne oslabitve, se bosta obe ojačitvi ničelnega reda (n=0)
takorekoč pokrivali (glej spodnjo sliko). Če pa je zorni kot med njima j1,
pa pade ojačitev ničelnega reda druge zvezde v smer oslabitve prve zvezde
in to bo že dovolj velik kot za razločevanje obeh zvezd. Seveda bi lahko
zdaj trdili, da se pa lahko pojavijo težave, ko sovpadejo različne ojačitve
dveh ali večih zvezd. To se sicer dogaja a ponavadi tega sovpadanja ne opazimo,
saj je gostota svetlobnega toka višjih interferenčnih redov precej manjša od
ničelnega reda (glej sliko). Ta grob razmislek za režo nas je pripeljal do
rezultata, ki le malo odstopa od rezultata za krožno odprtino. Za režo torej
velja, da je kot pod katerim še ločim dve zvezdi enak kotu prve oslabitve, v
smer katere pade maksimum ene izmed zvezd: j0=j1=l/D.
(SL_ Stran 601 Principles of physics, fig. 25.8., VAŽNO)
Če namesto širine D privzamemo premer objektiva (2R), dobimo zvezo za ločljivost
j0=l/(2R)=0,5*(l/R), kar pa je zelo blizu rezultatu za krožno odprtino
(j0=0,61*(l/R)). Pravilen in precej bolj zapleten račun za krožno odprtino
teleskopa vključuje Besslove funkcije, a naš rezultat in predvsem preprost
razmislek sta čisto dobra za razumevanje fenomena ločljivosti optičnih naprav.
Vrnimo se k rezultatu. Ločljivost torej omejuje valovna dolžina in premer
objektiva. Valovna dolžina elektromagnetnega valovanja, ki jo zazna človeško
oko je med 400nm in 700nm. Ločljivost v vidnem delu elektromagnetnega
valovanja bomo torej povečali, če bomo gradili teleskope z velikimi
premeri. Za primer izračunajmo ločljivost človeškega očesa (premer
zenice čez dan je približno 2mm) in ločljivost amaterskega teleskopa
s premerom objektiva 20 cm, za svetlobo valovne dolžine 500nm.
jočesa=0,61*(l/Ročesa)=0,61*(0,5*10-6m/0,001m)rad=0,000305rad,
to je približno
(0,000305*180*360"/p=63") 1 ločna minuta ali šestdesetina ločne
stopinje. joteleskopa=0,61*(l/Rteleskopa)=0,61*(0,5*10-6m/0,1m)rad=0,0305rad,
to je 100 krat manjši kot glede na ločljivost očesa ali približno 0,6 ločne sekunde.
Komponenti zvezde Mizar, zvezdi A in B sta narazen 14", bomo z
20-centimetrskim teleskopom brez težav ločili med sabo, a prosto
oko bo videlo dvojno zvezdo kot enojno. Z očesom vidimo recimo
Saturn kot točkasto telo, saj zorni kot planeta ob opozicijah
ne presega 20 ločnih sekund, obročki pa ne presegajo 50 ločnih
sekund, z amaterskim teleskopom pa vidimo Saturn v vsej njegovi
lepoti, planet in obročki so, kot da bi planet opazovali iz
neposredne bližine. Z očesom vidimo recimo postaji Mir in
Shuttle kot točkasti telesi, s teleskopom pa že vidimo njuni
obliki. Dolžina Shuttlea je 37m in v primeru, da je v orbiti postaje
Mir (okrog 350km nad Zemljo), je zorni kot čolnička (37/350000)rad,
kar znaša 22 ločnih sekund in v okularju teleskopa že lahko razločimo
obliko čolnička. Upam, da so bili primeri skupaj s fizikalnim ozadjem
dovolj nazorni in prepričljivi v smeri razumevanja optične podobe sveta.
Tudi velikost in razdalja fotoobčutljivih receptorjev v človeškem očesu
na mrežnici je prilagojena ločljivosti ene ločne minute. Narava torej
ne razmetava z gostoto receptorjev, zdi se, da je vse "optimalno"
usklajeno med sabo in, da se pogojuje.
Vrnimo se k spektrografiji. Kako bi ocenili ločljivost
pri spektrografu na uklonsko mrežico s pomočjo že povedanega
o fenomenu uklona? Če nam prav uklon omogoča razstavljanje
svetlobe na posamezne valovne dolžine, pa nam hkrati tudi
omejuje ločljivost. Ločljivost spektrografa na uklonsko mrežico
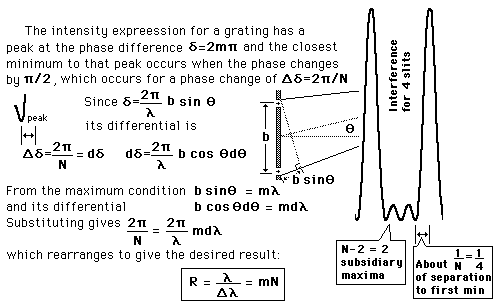
se izračuna po enačbi: Dl/l=1/(nN), oziroma Dl=l/(nN). N je
uklonski red, n število rež, l valovna dolžina pri kateri
določamo ločljivost, Dl razlika med valovnima dolžinama,
ki ju med sabo še ločimo. Poglejmo ali bi lahko uporabili
naše znanje in do povezave prišli sami, naše razmišljanje
bo groba poenostavitev Fraunhoferjevih in Fresenelovih
računov. Svetloba pade na uklonsko mrežico po celotni širini
D, ki je kar enaka številu rež (n) krat razdalja (d) med
sosednjima režama (D=n*d). Vsekakor se poleg interference
svetlobe zaradi uklona na posameznih razah, ki sestavlajo
mrežo, pojavi še uklon na skrajnih robovih mrežice. Mrežica
ima širino D in ločljivost mrežice ne more biti večja kot jo
določa uklon na odprtini širine D. Če hočemo ločiti dve valovni
dolžini med sabo, potem mora biti razlika valovnih dolžinah vsaj
tolikšna, da se oslabitve zaradi uklona na robovih mrežice širine
D ujemajo z interferenčnimi maksimumi sosednje valovne dolžine.
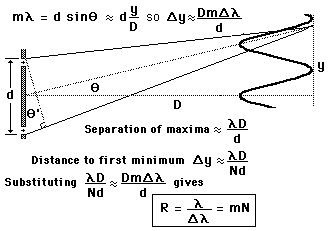
Ločljivost za režo D je, kot smo izpeljali, j0=l/D=l/nd. Po
interferenčni enačbi, so smeri ojačitev za valovno dolžino l
določene za majhne kote s pogojem jN=Nl/d. Če se valovna
dolžina sosednje črte razlikuje za Dl, potem sprememba
smeri ojačitve DjN=NDl/d ne sme biti manjša od ločljivosti
celotne širine D mrežice (j0=l/nd). V mejnem primeru torej
velja, da je j0=DjN ali NDl/d=l/nd. Iz zadnje zveze sledi,
da je ločljivost enaka Dl/l=1/(nN), oziroma, da razlika med
sosednjima valovnima dolžinama, ki ju želimo med sabo še
ločiti v bližini valovne dolžine l, ne sme biti manjša
od Dl=l/(nN). Ponovimo, veliki N je red ojačitve, n pa
število rež. Večji je N večja je ločljivost, vendar
ponavadi spekter merimo pri N=1, saj gostota
svetlobnega toka pri višjih redih močno pade.
Iz povedanega sledi, da je z uporabljeno uklonsko mrežico s
približno n=36mm*530/mm=19000 režami možno pri 400nm in prvem
uklonskem redu (N=1) razločiti valovni dolžini, ki sta narazen
za Dl=l/n=400nm/19000=0,02nm, to je pa že zelo spodobna
ločljivost. To pomeni v grobem, da če bi mi hoteli izkoristiti
maksimalno ločljivost mrežice, bi morali načeloma zaslon (film)
v našem primeru odmakniti od mrežice vsaj za nekaj 10m. V tem
primeru se tudi na zaslonu ustrezno poveča razpon spektra in
sedaj vemo, zakaj po knjigah najdemo neverjetne slike, ko so
posnetki spektrov dolgi cele metre, glej spodnjo sliko. Danes
spektre snemajo s CCD kamerami, in to po korakih.
(Sl_ ,Prosi Bojana za sliko z meterskimi posnetki spektrov, VAŽNO)
Izdelava preprostih spektrografov in snemanje spektrov (4)
Kaj je sploh barvni spekter? Na začetku smo že omenili, da je to,
povedano poenostavljeno, vsem dobro poznana mavrica, v kateri se
recimo Sončna svetloba razstavi po barvah, lahko rečemo tudi po
valovnih dolžinah, oziroma frekvencah. Ker pa večina svetil, razen
plinskih in laserjev, oddaja zaradi termičnih in mnogih drugih razlogov,
zvezni spekter, so v mavrici zastopane takorekoč vse barve, se pojavi
vprašanje, kaj nam poleg estetskega užitka nudi taka barvno razstavljena svetloba.
Mnogi članki v astronomskih revijah že nekaj časa opozarjajo na
izjemen pomen Sonca, tudi Spika. Kaj je Sonce? Sonce je nam najbližja
zvezda. Brez Sonca ne bi bilo ne našega planeta, ne nas, ki zelo radi
pozabimo na veliko plinsko gmoto (Sonce) in se raje oziramo za oddaljenimi
zvezdami, ne da bi se večina sploh zavedala, da so drobcene svetleče
pikice na večernem nebu, pravzaprav "Sonca". Nikakor nočem odrekati
izjemnega pomena opazovanjem in merjenjem na nočnem nebu, a včasih
hočemo izvedeti več o zvezdah, ki so stotine milijonov daleč, a na
Sonce, ki nam to isto nudi z neprimerno manj truda in sredstev sploh
ne pomislimo. Posebej to velja za osnovno in srednjo šolo, kjer je
oprema ponavadi nadvse skromna, a želje po raziskovanju dokaj velike
in Sonce se kar samo ponuja, da ga vsaj v okviru možnosti raziščemo.
Tudi na Gimnaziji Šentvid se občasno "zgodi" kakšna raziskovalna
naloga iz astronomije. Ena izmed nalog se je tudi ukvarjala s
slikanjem spektrov zvezd. Naloge sta se lotila Jure Cedilnik in
Damjan Šterk. Seveda so bile ambicije na začetku zelo velike,
podkrepljene s številnimi krasnimi slikami iz astronomskih
knjig. Lotila sta se tudi izdelave Rowlandovega ??? spektrografa
(uklonska mrežica na konkavnem zrcalu, na katerega pade
vzporeden snop svetlobe, ki se odbije in zbere v gorišču,
hkrati pa mrežica razkloni svetlobo na spekter, glej sliko ).
Ena izmed metod je bila tudi namestitev uklonske mrežice
pred vhodno odprtino teleskopa. Mrežica je bila narejena z
računalnikom. Mrežico so sestavljale vzporedne 0,5mm široke
črte približno mm narazen, ki smo jo kar s pc-ja printali
na folijo (zadostuje tudi fotokopiranje s papirja na folijo).
Po pričakovanju (izračunu) je bilo moč videti v okularju
teleskopa spektre zvezd, široke do 3 ločne minute, a kaj
več kot to se nismo potrudili. Vsekakor pa je bilo v
okularju lepo videti zvezdice in zraven njihove mavrične barve.
(SL_ , Slika Rowlandovega ??? spektrografa, nekaj besed o principu. )
Rowlandov spektrograf je načeloma deloval, vendar so se pojavljale
težave z montažo, veliko filma porabi taka naprava itd., zato smo
iskali dodatne poenostavitve. V literaturi se tudi najdejo opisi
objektivnih in okularnih spektrografov na prizmo, a na uklonsko
mrežico nismo zasledili nobenega. Takoj smo poiskali rešitev za
zvezdice na nočnem nebu, ki so načeloma točkaste (zaradi refrakcije
v različno toplih plasteh ozračja se svetloba nekoliko razprši).
Uklonsko mrežico smo kar montirali neposredno pred objektiv
(stari dobri selotejp je zadostoval) in zvezdice so pustile
svoj spekter na filmu. Postopek je zelo enostaven, eksponirala
sta nekaj minut, tako da je zvezda zaradi vrtenja Zemlje na
filmu, pustila sled, ki jo je uklonska mrežica razklonila v
spekter. Iz ljubljanske preosvetljene kotline sta sicer
dobila nekaj absorbcijskih črt, a ločljivost ni bila kaj
prida, saj je nebo preosvetljeno, glej sliko.
(SL_ Posnetek iz raz naloge, Spekter zvezde ??? Uklonsko
mrežico smo montirali kar neposredno pred objektiv (stari
dobri selotejp je zadostoval) in zvezdice so pustile svoj
spekter na filmu. )
Za Sonce tak način ni primeren, ker je zaradi svoje bližine
zorni kot prevelik, da bi ga lahko obravnavali kot točkasto
telo, pa tudi svetlo nebo ni primerno za ozadje. Odločili
smo se, da izdelamo lasten objektivni spektrograf na mrežico.
Ideja je bila naslednja. Na razpolago smo imeli naslednja sredstva:
-zrcalni fotoaparat in objektive 50mm, 135mm in 200mm
-stojalo
-dve uklonski mrežici
-papir, lepilo, folijo iz aluminija, britvici
-plina vodik in helij
Svetlobo naj ukloni mrežica tik pred objektivom. Na filmu naj bi bil
spekter porazdeljen po celotni dolžini, okrog 3 cm (leica format).
Spekter bi naj predstavljala z uklonsko mrežico razklonjena slika
reže, skozi katero padajo Sončni žarki. Absorbcijska črta je torej
načeloma slika reže, bolje rečeno, je temnejša črta zaradi pomanjkanja
svetlobe "točno" določene valovne dolžine med svetlimi črtami (slikami)
reže. Režo smo naredili iz dveh britvic na koncu papirnatega tulca ovitega
z alu. folijo. Dolžina tulca je bila okrog enega metra, toliko da se je že
dalo skozi objektive ujeti ostro sliko reže. Kako bi določili širino slike
reže? Boljši spektrografi brez težav ločijo med sabo 10000-inke nm in so
zaradi izjemne natančnosti nenadomestljivi inštrumenti. Mi bi se zadovoljili,
glede na podatke iz spodnje tabele, že z ločljivostjo 1nm, da bi ujeli
najizrazitejše absorbcijske črte vodika, magnezija, helija, železa,
kalcija, natrija. Če predpostavimo začetek spektra pri 400nm in konec
pri 700 nm, potem lahko na 30mm dolžine filma v našem primeru stlačimo
(700nm-400nm)=300nm. Torej, če želimo ločiti barve vsaj z
natančnostjo 1nm, potem pripada enemu nanometru na filmu
širina 0.1mm. To pa je velikostni red, ki ga z očesom že
zaznamo, sploh pa, če diapozitiv projeciramo na zaslon,
kjer bo celotni spekter povečan za nekaj 10-krat. Kotna
ločljivost človeškega očesa je namreč ena ločna minuta,
kar pa načeloma pomeni, da na bližnji razdalji očesa
(25cm) ločimo črti, ki sta narazen za 250mm*(1'*p/10800')=0.07mm.
Kar se tiče filma pa vsekakor velja, da je črta na filmu lahko le
toliko tanka, kot je tipična velikost zrn emulzije na filmu.
Velikost zrn je tipično nekaj mikrometrov, tako da debelina
črte 0.1mm večkratno presega ločljivost filma, kar nam ustreza.
V glavnem se najizrazitejše absorbcijske črte navedenih elementov
iz tabele pri tej ločljivosti med sabo ne bodo prekrivale, saj so
večinoma narazen za več kot nm. Iz zahteve po ločljivosti (enemu
nanometru pripada na filmu 0,1mm) se tudi preračuna širina vhodne
reže. 0,1 mm široka slika reže ne pomeni, da bo v resnici na sliki
črna črta te debeline, saj se bo le ta slika prekrivala s slikami
sosednjih valovnih dolžin, razen mogoče pri črtah kalcija, ki so
široke več kot nm. Poglejmo grobe račune za "najcenejši" spektrograf.
Fotografirali bomo spekter prvega reda, to je prvi razklon svetlobe za
ničnim redom, ki ga predstavlja neuklonjen del svetlobe, glej sliko.
Velja torej že opisana enačba za uklon na mrežici:
sinj=l/d
Če si izberemo objektiv f=13,5cm in mrežico 530 rež na mm (d=1mm/530),
potem približno velja (gre za oceno dimenzij in slike spektra
spektrografa), da je razdalja b od mrežice do zaslona kar
približno goriščna razdalja objektiva. Oziroma, če je razdalja
reže od mrežice (objektiva) a=1m relativno majhna, potem iz
znane enačbe 1/a+1/b=1/f, dobimo za b nekoliko večjo vrednost
b=15,6cm. Če se grobo omejimo na spekter med valovnima dolžinama
l1=400nm (vijolična svetloba) in l1=700nm (rdeča svetloba),
potem se bo spekter začel z rdečo svetlobo pod kotom
j1=arc(sin(l1/d))=12,2o in končal z vijolično barvo
pri kotu j2=arc(sin(l2/d))=21,8o glede na ničelni
red. Razdalja x1=b*tgj1=3,37cm=3,4cm in razdalja
x2=b*tgj2=6,24cm=6,2cm, Dx=x2-x1=2,8cm, kar ustreza
našim pričakovanjem glede na dolžino leica ????? formata.
Zdaj lahko tudi izračunamo odprtino vhodne reže.
Iz geometrije nastanka slike pri zbiralni leči velja:
(širina reže)/(širina slike reže)=a/b, iz česar sledi,
da je širina reže=(a/b)*(širina slike)=(100/15,6)*0,1mm=0,6mm.
(SL_, Nariši skico za izračune zgoraj.)
V resnici smo mrežico postavili pred objektiv, torej je razdalja
b nekoliko večja od izračunane in tudi aprat smo zasukali približno
za kot (j1+j2)/2=17o tako, da se je spekter porazdelil po celotnem
posnetku. S tem sice pride do majhnih sprememb, saj centralni vpadni
žarek več ne pada pravokotno na spekter (glej sliko), kar v grobem
pomeni, da se je tudi razdalja med režami v mrežici za svetlobo
zmanjšala (v resnici je treba spet upoštevati razliko poti, ki se
sedaj izračuna nekoliko drugače kot pri pravokotnem vpadu), a širina
spektra na filmu se ni bistveno spremenila, saj smo v tem primeru tudi
zaslon (film) zasukali za 17o, tako da ocene našega računa še zmeraj
dokaj dobro držijo.
(SL_ , Nariši skico za tekst zgoraj, fotoaparat, mrežica, tulec z
režo, film ....)
V resnici smo s pogledom skozi kukalo fotoaparata sami centrirali
spekter, kot in tudi širina spektra sta res ustrezala izračunanemu.
Kar je še bolj pomembno in tudi lahko zelo uporabno (recimo za spretnega
izdelovalca učil) je, da so se absorbcijske črte videle kar skozi
kukalo fotoaparata. Kaj bi si še želeli več ob skromnih sredstvih
vloženih v napravo. Uklon na vhodni reži ni motil slike, saj so
maksimumi uklona na reži precej bliže simetrali reže (Zakaj, sledi
iz enačbe sinj=nl/d.) in je gostota svetlobnega toka pod koti 10 ali
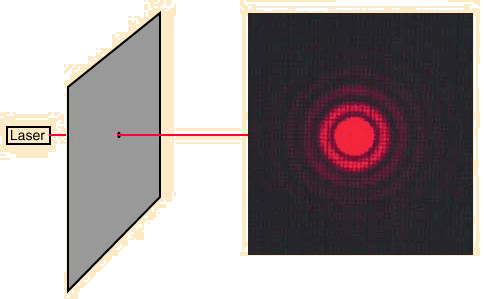
več stopinj zanemarljiva. S pomočjo interference laserske svetlobe
znane valovne dolžine, smo tudi preverili gostoto mrežice. Mrežico
smo postavili pred izhodno odprtino laserskega žarka in na oddaljeni
steni izmerili uklon, izmerjene podatke smo vstavili v enačbo
(d=sinj/(Nl)) in dobili rezultat 530 rež na mm z napako
plus_minus nekaj rež. Tudi grob sklep, da če svetloba ne
pade pravokotno na mrežico, se le ta obnaša podobno, kot
da bi povečali gostoto mrežice, oziroma zmanjšali razdaljo d,
smo eksperimentalno z laserjem potrdili.
Zdaj je seveda nastopil trenutek snemanja.
Rezultati so bili super, seveda nismo porabili
kaj dosti časa in denarja, za snemanja z različnimi
dia filmi, kar bi bilo prav, ker vsi filmi niso enako
občutljivi za določene barve. Takoj smo se vprašali, ali
so temnejše črte v spektru res posledica našega pravilnega
razmišljanja, ali pa je to bolj "srečno" naključje in na filmu
vidimo zgolj črte kakega drugega efekta. Spekter je bil zelo
podoben tistim iz knjig. Ali ga lahko še kako umerimo? Ja, z
isto mrežico, zdaj brez vhodne reže, smo posneli steber
svetlečega vodikovega plina, ki ga premore skoraj vsaka
srednja šola. Ker je cevka s plinom tanka, debela le 5mm,
smo se oddaljili od svetlečega plina za toliko, da je bila
debelina črte na filmu 0,1mm. Iz geometrije zbiralne leče
sledi račun za razdaljo a: a=(5mm/0,1mm)*b=7m, če za b=13,5cm privzamemo
kar goriščno razdaljo teleobjektiva, kar je pri veliki razdalji do
predmeta smiselno. Spektrograf je zdaj samo mrežica na teleobjektivu,
saj smo tulec z režo sneli, ker reža samo omejuje količino vpadle svetlobe.
Slikali pa smo v temi, le vodik je medlo svetil. Vodikove črte si sledijo
takole (glej sliko): Hdelta= 410,17nm, Hgama=434,05nm, Hbeta=486,13nm,
Halfa=656,28nm.
(SL_ , Slika vodikovih črt, diapozitiv)
Kako primerjamo laboratorijski spekter s Sončevim? Pri enaki povečavi z
diaprojektorjema se na zaslonu brez velikega truda opazi sovpadanje
laboratorijskih emisijskih črt s Sončevimi spektralnimi absorbcijskimi
vodikovimi črtami. Za natančnejšo umeritev so seveda štiri vodikove črte
premalo, a če narišemo umeritveni graf, nam vodikove črte lahko pomagajo,
da brez večjih težav najdemo črte nekaterih že zgoraj navedenih elementov.
Lege vodikovih črt so nanešene v pripadajoči barvi, lege ostalih pa v črni.
Ni težko opaziti, da bi krivulja, s katero bi povezali točke, bila zelo blizu
premice, kar tudi ni težko izpeljati s pomočjo srednješolske trigonometrije,
ki tudi da za majhne kote enak rezultat. Tisto, kar je razveseljivo je,
da je pri projekciji bilo moč brez večjega naprezanja našteti vsaj 60 črt.
To pa seveda ne pomeni, da smo s tem tudi zaznali prisotnost 60 elementov v
Sončevi atmosferi, saj enemu elementu pripada več črt, recimo vodiku štiri
v vidnem delu spektra. Seveda je zaradi skromne izkoriščenosti sicer solidne
ločljivosti naše uklonske mrežice s tem spektrografom nemogoče razločiti
črte vseh ostalih elementov. Vsekakor je potrebno povdariti, da tudi atmosfera
Zemlje absorbira del svetlobe. Na Soncu je s pomočjo spektrografije bilo
odkritih nad 60 elementov, helij so celo prej odkrili na Soncu (leta 1868)
kot na Zemlji (leta 1895). Čeprav ne spada direktno v ta kontekst, pa vendar.
Od kod pa sploh prihajajo težki elementi, saj meritve kažejo, da sta
v vesolju najizraziteje zastopana vodik in helij? Gotovo so težji
elementi, kot smo že omenili, produkt zlivanja (fuzije) lažjih jeder
v težja (vodika v helij, helija v berilij, ogljik .....) in glavni
proizvajalec težjih elementov so zvezde z veliko maso, ki ponavadi
končajo v eksploziji znani z imenom supernova. Koliko se jaz spomnim,
smo v raznih šolah veliko prekladali atome sem ter tja, a o izvoru,
"alkemiji" težkih elementov, nismo slišali prav nič. Škoda, da je
astronomija s svojimi temeljnimi spoznanji o izvoru materije tako
skromno zastopana v šolskih programih. Če pogledamo sestavo človeškega
bitja, potem velja, da smo se vsekakor najprej "rodili" v zvezdah in
tega otrokom ne smemo zamolčati.
(SL_ Slike spektra:
1.Umeritveni graf spektra s posnetkom spektra, razvij fotografijo,
jo prilepi na excelov graf in
skeniraj
2. Izsek iz kalcijevega dela spektra.
DODAJ KMENTARJE ...)
Potrebno je omeniti in povdariti, da je dijak Gregor Zaletel vzporedno
z obravnavano nalogo meril spekter Sonca s prizmo. Uporabil je različne
prizme, ki so bile dosegljive na šoli. Rezultati so pokazali, da je z
neprofesionalno prizmo bistveno težje dobiti podobne rezultate kot
jih da uklonska mrežica. Vsekakor je nauk ta, da je za Sonce bistveno
bolj uporabna, učinkovitejša in cenejša uklonska mrežica, saj so
kvalitetne prizme zelo drage.
(SL_ Astronomy, stran 69, slika 4-44. Zelo poučno in enostavno je,
če učencem pokažemo, da je že odboj svetlobe od raz CD plošče dovolj,
da pride do interference. )
=====================================================================
Morebitna varianta zaključka
V prispevku je veliko tem načetih, a le valovanje in fenomen uklona
sta podrobno obdelana, kar je poleg predstavitve spektra bil tudi
glavni namen teksta. Za zaključek pa bi dal en majhen izziv za
tiste navdušene amaterje, ki se želijo soočiti z uporabo matematično
zapisanih modelov delovanja narave. Tem modelom rečemo tudi zakoni,
kar velikokrat naredi predvsem na laike napačen vtis. Želim si, da
iz teksta potegnete podatke in matematične povezave in s pomočjo
njih še enkrat izračunate temperaturo na Soncu in valovno dolžino
svetlobe, pri kateri seva Sonce najmočneje. Ta dva podatka sta namreč
zelo vplivala na smer razvoja življenja na Zemlji, torej tudi na človeka,
saj ni slučaj, da so naše oči prilagojene in najbolj občutljive prav na
barvo prehoda med rumeno in zeleno. Sončni žarki so nam omogočili, da
danes o njih razmišljamo in se grejemo v njihovi "toploti". Uporabite
Štefanov in Wienov zakon, poiščite razdaljo do Sonca in polmer Sonca
in gostoto svetlobnega toka (j), ki pade na naš planet. To so namreč
podatki, do katerih s(m)o se najprej dokopali, in ki jih je Štefan
lahko kot prvi uporabil za izračun temperature Sonca. Res je nekaj
enkratnega, vsaj za ljudi s smislom za čudenje, da znamo izračunati
temperature in določiti sestavo nebesnih objektov, do katerih nikoli
ne bomo prišli, če pa bi, pa bi se večinoma v trenutku spremenili v
plin, z vsemi spektralnimi barvami. To je seveda klasična lahka
fizikalna naloga, v kateri pa se skrivajo stoletja nabiranja znanj
in naravoslovnih izkušenj, mnogokrat nerazumljenih in prezrtih ljudi.
Če naloge ne boste opravili, kar predvidevam, nič zato, že to je rezultat,
da se soočite z izzivom, ki so ga prestali le najvztrajnejši v človeški
zgodovini.
{Zaključek in še kaj bom dopolnil ali spremenil, dodal bom še sliko
leče in pot žarkov ter razmerja med a, b, p in s.}
Zorko Vičar
=====================================================================
SAMO SHEMA.TKSTA, ki ne gre direktno v tekst !!!!!!!!!!!!!!!!!!!!!!!
Pomoč - načrt.
Opis Sonca, kratek.
Kako nastane svetloba, daj tudi grafe prehodov in tudi primr iz knjige o
spektrih (emisijskih in absorbcijskih). Omeni tudi Petra mihorja in njegovo
animacijo kot primer lažje predstavitve, s tem boš tudi njega vključil (mozna resitev).
Kako naredimo svetlobni spekter?
(ŽE) Kako nastane črtast spekter (Fraunhofer ???)? Fraunhofer Joseph 1814 s
spektroskopom na prizmo odkrije okrog 600 spektralnih črt, danes jih poznamo
milijon. (Universe stran 90, slika Son. spektra, spektri nekaterih plinov in
elementov stran 79)
Kako deluje uklonska mrežica?
Ali tudi zemeljska atmosfera absorbira e.m. valovanje?
Kaj sklepamo iz spektra zvezd, glej Vujnoviča?
Dodaj slike spektra, ki leži v metrih na tleh in zraven še stoji astronom!
Daj preračune in ujemanje s slikami v tekst (dolžino spektra na diapozitivu)?
Ali boš omenil Gregorja, ki je delal na prizmo ????, da težava so rezultati, ki
niso zmeraj
izpolnili pričakovanj in šolska selekcija, ki mora zadostiti v naprej določenim
kvotam, ki je po svoje utemeljena, a mnogokrat prizadane raziskovalce tako močno,
da nehajo z raziskovanjem in izgubijom vse iluzije o znanosti, ki jih prav šola
prodaja kot svoj temelj in deloma tudi cilj. Slisal sem za zgodbo, ko se na neki
soli niso hoteli prikloniti selekciji in so dijake za zagovor kar zrebali in se
to so celo prepustili drugi ustanovi..
Teleskop za x žarke (Astronomy stran74)
CD plosca in uklon na njej (astronomy stran 69, slika 4-44).
Sateliti in Zemlja recimo Astronomy stran 35.
Zanimiv posnetek mrka in nastanek Astronomy 116.
Karta mrkov, Astronomy s tran 119.
Nastanek valov, Universe starn 148
Nariši lepo barvno sliko spektra za članek z mrežico zaslonim x1 in x2 …
Uklon na vhodni reži ni motil slike, saj so maksimumi uklona na reži precej
bliže simetrali reže (zakaj, sledi iz enačbe sinj=nl/d) in je gostota svetlobnega
toka pod koti 10 ali več stopinj zanemarljiva.
Glej strani 68 in 69 o Soncu in elementih ... v knjigi Nebo in zvezde.
Povečaj kalcijevi črti, ker sta zelo didaktični in ju predstavi, kot posebno
zelo pomembno sliko, tudi zaradi širine absorbcijskih črt.
Povej kaj o izvoru razširjenosti črt.
TISTI KI NE VEDO KAJ POMENI (rec. INTERFERENCA) NAJ BEREJO ČLANEK NAPREJ,
OSTALI pa naj gredo na naslednje poglavje … TO NAJ BO SISTEM ČLANKA, rešitev
za razlago!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
S pomočjo interference (d=sinj/(Nl)) laserske svetlobe znane valovne dolžine,
smo tudi preverili gostoto mrežice, 530 rež na mm z odstopanjem nekaj rež. Tudi
naš sklep, da če svetloba pade pod kotom, glede na pravokotnico na mrežo, se le
ta obnaša podobno, kot da bi povečali gostoto mrežice, oziroma zmanjšali razdaljo
d, smo eksperimentalno z laserjem potrdili..
???? sledi vprašljiva vsebina…. Zdaj tudi vemo, da je prednost Rowlandowega
spektrografa prav v ločljivosti. Pri goriščni razdalji uklonskega zrcala 0,5m,
ki svetlobo razdeli v vsaj pol metra dolg spekter, je razmerje
5000 desetink mm proti 3000 desetink nm tako, da je na desetinko mm
mogoče doloćiti valovno dolžino vsaj na desetinko nanometra. To pa pomeni,
da bi brez težav ločili recimo črti železa b3 in b4 (516,89nm in 516,75nm),
kar pri naši izvedbi objektivnega spektrografa ni bilo mogoče. Ta del naloge
še čaka na izvršitev.
(POGLEJ v VUJNOVIČA-stran32 za kalcij in 66 in 46).
Za astronomski krožek: ZORKO Vičar
Komentarji so zaželjeni.
(SL_16 Universe stran 90, slika Son. spektra, spektri nekaterih plinov in
elementov stran 79)
Joseph Fraunhofer 1814 s spektroskopom na prizmo odkrije okrog 600 spektralnih
črt, danes jih poznamo milijon.
Oznaka Izvor(at., mol.) valovna dolžina (nm) Širina črte (nm)
K Ca+ 393,3682 (393,3666) 2,0253
H Ca+ 396,8492 (396,8468) 1,5467
Fe 404,5825 0,1174
h (d) H 410,1748 (410,1735) 0,3133
g Ca 422,6740 (422,6728) 0,1476
G Ca 430,7741
G Fe 430,7906
G' (g) H 434,0475 (434,0465) 0,2855
e (ponekod d) Fe 438,3547 (438,3557) 0,1008
Fe 440,4761 0,0898
D Fe 466,8140
F (b) H 486,1342 (486,1327) 0,3680
C Fe 495,7609
b4 Mg 516,7327 (516,7343) 0,0935
b4 Fe 516,7491
b3 Fe 516,8901
b2 Mg 517,2698 (517,2699) 0,1259
b1 Mg 518,3619 (518,3618) 0,1584
E2 Fe 526,9541
D3 He 587,5618
D2 Na 588,9973 (588,9953) 0,0752
D1 Na 589,5940 (589,5923) 0,0564
a O2 (atmosfera Zemlje) 627,6-628,7
C (a) H 656,2808 (656,2816) 0,4020
B O2 (atmosfera Zemlje) 686,7-688,4
A O2 (atmosfera Zemlje) 759,4-762,1
Od septembra 1999 je stran obiskalo
ljudi.
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si
Nazaj na domačo stran.