Svetlobno onesnaženje in astronomija - raz. naloga

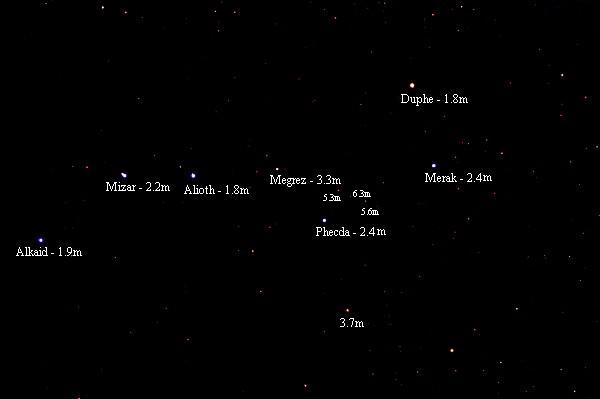
Vidnost Velikega voza glede na osvetljenost neba (poučna animacija).


Ugotavljanje nebesnega sija; Walkerjev zakon
Kljub dejstvu, da svetlobno vznemirjanje astronomom povzroča velike skrbi,
pa obstaja le malo poročil o raziskavah kvalitativnih in kvantitavnih vidikov
motenj astronomskih opazovanj zaradi svetlobe. Največ jih temelji na Walkerjevem
delu (1973). Običajno se svetloba, ki moti astronomska opazovanja, pojavlja v
obliki nebesnega sija v bližini velikih urbanih, industrijskih ali kmetijskih
koncentracij. Svetlost nebesnega sija lahko primerno izrazimo z "Walkerjevim
zakonom", ki ga je mogoče zapisati kot
log I = - 4,7 – 2,5 log R + log F
(po: Anon., 1984; prim. Walker 1973, 1991), kjer je p razmerje med opazovanim
nebesnim sijem, kot ga izmerimo v smeri vira pod kotom 45°, in naravnim sevanjem
ozadja, R je razdalja do vira (v km), F pa celotni svetlobni tok zunanje razsvetljave
pri viru (v lm). Omeniti moramo, da obstaja nekaj dvomov, ali je kot 45° najprimernejši;
največ opazovanj gre navzdol do 30° ali celo 15°. Slednji kot se na Nizozemskem
uporablja za opisovanje bolj splošnega vpliva nebesnega sija na izkušnje ljudi
v okolici njegovih virov (Anon., 1997; Van Berghem-Jansen, 1997). Za sevanje
ozadja se običajno vzame 2 . 10-4 cd/m2. Ta zakon je bil vpeljan za mesta
na jugozahodu ZDA. Zdi se, da ga je mogoče uporabiti tudi za druge kraje
(Fisher&Turner, 1977; Garstang, 1991; Isobe & Kosai, 1994; Isobe, 1997;
Sanchez Beitia, 1983).
Walker (1991) predpostavlja, da je skupni svetlobni tok nekega mesta
premo sorazmeren s številom njegovih prebivalcev, namreč 1000 lm na
prebivalca (prim. tudi Schreuder, 1991). Za razširitev modela za širšo
uporabo, natančneje glede približka 1000 lm na prebivalca, potrebujemo
več podatkov. Finch et al. (1980) so predlagali vrednosti med 500 in
1000 lm na prebivalca, Schreuder (1987) pa ugotavlja, da je mogoče
najti tudi vrednosti, ne višje od 50 lm na prebivalca, čeprav je
znašalo poprečje njegovega vzroca iz vsega sveta priblilžno 850 lm.
Drugo, matematično strožjo izpeljavo, podajajo Fellin et al. (2000).
Predstavili so relacijo, ki dovoljuje določanje porasta magnitude praga
za ravno še vidne zvezde kot rezultat parametrov razsvetljave:
dM = - 2,5 log (1 + Rn / [r(1 - Rn )],
kjer je
The formula we use to estimate urban sky glow is called "Walkers
Law". It was proposed by Merle Walker based on his measurements of sky
glow for a number of cities in California. It can be used to estimate the
sky glow at an observing site, looking at a zenith angle of 45 degrees
toward an urban source d kilometers away. The formula is
I = 0.01Pd-2.5
where I is the increase in sky glow level above the natural background
and P is the population of the city
and d is the distance to the center of the city in km
For example, I = 0.02 means that the sky background is 2% above the
natural background midway between the horizon and the zenith in the direction
of the city, and 1.00 means that the sky glow is double the natural background,
a 100% increase. The equation seems to best fit communities where the average
lumens per person is between 500 and 1000. Large cities emit more light
per person, and the amount of skyglow may be larger than the formula shows,
perhaps. For example, a city with a population of 1,000,000 that is 100
km from an observing site may produce more sky glow than the 10% the formula
indicates. Example 1: We can calculate the urban population at which
the sky glow will be 10% above the natural background, for a given distance
of the observatory from the city. At this sky glow level, significant sky
degradation is beginning.
Distance (d): 10 km
25 km 50 km 100 km
200 km
Population: 3,160
31,250 177,000 1,000,000 5,660,000
Example 2: Consider the sky glow impact at Kitt Peak, due to
these cities:
Population Distance
I is therefore
Tucson
500,000
60 km
0.18 (an 18% increase)
Phoenix
1,250,000 160 km
0.04
Sells
5,000
16 km
0.05
If Tucson grows to 1,000,000, then I = 0.36, and if growth in the Avra
Valley (d = 30 km) leads to a 250,000 population, then I = 0.51 for that
alone. We must try to insure a lower sky glow. It is easy to see
why one worries about growth, especially that which occurs close by the
observatory. (We measure an increased sky glow of only 6% at present. Outdoor
lighting controls do work!)
Example 3: Effect of distance on the fall-off of sky glow:
Distance (r) 10
20 30 40 50
60 80 100 km
Light level 316
56 20 10
6 4 2
1
Note: The "natural sky glow background" level at the zenith is assumed
to be 2 x 10-4 cd m², or 21.6 mag. per arcsecond².
It is greater at a 45 degree zenith angle.
REDUCING OBTRUSIVE LIGHT Duco A. SCHREUDER Duco Schreuder Consultancies The following conversion into the ISO luminances (for photopic vision) is adopted: ‘a luminance of 3,2·10^-6 cd/m2 corresponds to 26,33 magnitude per arcsec2’. (CIE, 1997). The limiting magnitude follows from the definition of (difference in) magnitude: m=2.5 log (l1/l2), [4] where l1 and l2 are the luminous intensities of the two stars that are compared. See for details Sterken & Manfroid (1992). When assessing the influence of the sky glow, the smallest luminance for the most favorable conditions is Lo1 and under sky glow conditions Lo2. The background luminance is Lb and Lv respectively. With Lv=a·Lb, and according to [1] and [2], for ---- luminous - svetlost zvezde http://www.davidgilson.co.uk/academic/notes/html/astrphys.html - svetlost neba (Lv) je sestavljena iz naravnega ozadja (Lb) in umetne sipane svetlobe - izkaže se, da je smotrno svetlost neba izraziti z deležem naravnega ozadja, sorazmernostni koeficient je a: Lv=a*Lb Lb=2 x 10^-4 cd/m2, ali mb= 21.6 mag./ločsek.2 Po ISO standardu ustreza 3,2·10^-6 cd/m2 26,33 mag./ločsek.2 (CIE, 1997). Empirična povezava med svetlostima in magnitudama dveh svetil (zvezd) je: m2=m1+2.5*log10(L1/L2) Merle Walker based on his measurements of sky glow for a number of cities in California. It can be used to estimate the sky glow at an observing site, looking at a zenith angle of 45 degrees toward an urban source d kilometers away. The formula isMerle Walker je opravljal meritve svetlosti neba v bližini večih mest v Kaliforniji. Prišel je do empirične povezave, ki velja na razdalji d od središča mesta, v smeri 45 stopinj proti središču mesta. I = 0.01Pd-2.5
Kjer je: I je relativno povečanje svetlosti neba glede na naravno ozadje [ I=(Lv-Lb)/Lb = a-1] P je število prebivalcev v mestu d oddaljenost od središča mesta v km Primer za Ljubljano (300000 ljudi) d v km I 0.5 16970.6 1 3000.0 5 53.7 10 9.5 20 1.7 40 0.3 60 0.1 100 0.030 200 0.005 sprememba magnitude dm zaradi osvetlevanja neba Lv/Lb=(Lb+dL)/Lb=1+dL/Lb=1+I=1+0.01Pd^-2.5 mv=mb-2.5*log10(Lv/Lb) mv=mb-2.5*log10(1+I) mv=mb-2.5*log10(1+0.01Pd^-2.5) mb= 21.6 mag./ločsek.2 dm=mb-mv=2.5*log10(1+0.01Pd^-2.5) ****************** CIE je kratica za The International Commission on Illumination Sedež CIE je CIE Central Bureau Kegelgasse 27 A-1030 Wien Austria URL CIE: http://www.cie.co.at/cie/ Slovenija ni članica CIE, zanimivo, tudi ni članica ESA (The European Space Agency) =============== RAZSVETLJAVA 2002 LIGHTING ENGINEERING 2002 ZBORNIK PROCEEDINGS Največ jih temelji na Walkerjevem delu (1973). Običajno se svetloba, ki moti astronomska opazovanja, pojavlja v obliki nebesnega sija v bližini velikih urbanih, industrijskih ali kmetijskih koncentracij. Svetlost nebesnega sija lahko primerno izrazimo z "Walkerjevim zakonom", ki ga je mogoče zapisati kot log I = - 4,7 – 2,5 log R + log F F=N*500 lm N= št. prebivalcev 500 lm na enega, lahko je 100 do 1000. (po: Anon., 1984; prim. Walker 1973, 1991), kjer je p razmerje med opazovanim nebesnim sijem, kot ga izmerimo v smeri vira pod kotom 45°, in naravnim sevanjem ozadja, R je razdalja do vira (v km), F pa celotni svetlobni tok zunanje razsvetljave pri viru (v lm). Omeniti moramo, da obstaja nekaj dvomov, ali je kot 45° najprimernejši; največ opazovanj gre navzdol do 30° ali celo 15°. Slednji kot se na Nizozemskem uporablja za opisovanje bolj splošnega vpliva nebesnega sija na izkušnje ljudi v okolici njegovih virov (Anon., 1997; Van Berghem-Jansen, 1997). Za sevanje ozadja se običajno vzame 2 . 10-4 cd/m2. Ta zakon je bil vpeljan za mesta na jugozahodu ZDA. Zdi se, da ga je mogoče uporabiti tudi za druge kraje (Fisher&Turner, 1977; Garstang, 1991; Isobe & Kosai, 1994; Isobe, 1997; Sanchez Beitia, 1983). Walker (1991) predpostavlja, da je skupni svetlobni tok nekega mesta premo sorazmeren s številom njegovih prebivalcev, namreč 1000 lm na prebivalca (prim. tudi Schreuder, 1991). Za razširitev modela za širšo uporabo, natančneje glede približka 1000 lm na prebivalca, potrebujemo več podatkov. Finch et al. (1980) so predlagali vrednosti med 500 in 1000 lm na prebivalca, Schreuder (1987) pa ugotavlja, da je mogoče najti tudi vrednosti, ne višje od 50 lm na prebivalca, čeprav je znašalo poprečje njegovega vzroca iz vsega sveta priblilžno 850 lm. Drugo, matematično strožjo izpeljavo, podajajo Fellin et al. (2000). Predstavili so relacijo, ki dovoljuje določanje porasta magnitude praga za ravno še vidne zvezde kot rezultat parametrov razsvetljave: dM = - 2,5 log (1 + Rn / [r(1 - Rn )], kjer je dM: porast magnitude praga za ravno še vidne zvezde; Rn: skupni navzgornji svetlobni tok vsega mesta r: regijsko poprečje refleksijskega faktorja (po: Fellin et al., 2000, enačba 9). Nebesni sij je posledica svetlobe, ki se odbije navzgor in potem razsiplje nazaj na površje Zemlje. Del razsipane svetlobe se odbije naravnost navzgor. Običajno je to posledica slabo sprojektirane ali slabo nastavljene razsvetljave; lahko pa se pojavi tudi, če je svetloba namerno usmerjena navzgor. Še en pomemben prispevek k razsipani svetlobi pa daje svetloba, ki je sicer natančno usmerjena na osvetljevane predmete, vendar se od njih odbije. Cestne površine, trava in zgradbe odbijejo precejšen delež vpadne svetlobe, svetloba pa se običajno odbije navzgor. Poudariti moramo, da ta svetloba služi svojemu namenu le, če zadene opazovalčevo oko. V nekaterih primerih, kot npr. pri signalizaciji, je to svetlobni vir sam, skoraj v večini primerov pa je to svetloba, ki se odbija od "koristne" površine. Zato je predlog, ki ga je ponekod slišati, namreč, naj se vse površine prebarvajo črno, pa ne bo odbite svetlobe, v resnici nesmiseln, saj bi, četudi bi to zares storili – predvsem pa, če bi to bilo sploh mogoče –, bi postala razsvetljava popolnoma neuporabna. To velja še posebej za cestne površine. Vsem virom nebesnega sija, ki ga povzroča človek, pa je skupno eno: vsi predstavljajo gospodarske izgube. Crawford je na osnovi števila predpostavk "čez palec" izračunal samo v ZDA letne izgube v višini milijarde dolarjev (Crawford, 1991, 1997a). Isobe je postregel s podobnimi podatki, ki pa jih je potem podrobneje razdelal za specifična mesta in lokacije (Isobe, 1999). Prim. tudi Cinzano (1994, 1999, 2000) ter Cinzano & Diaz Castro (2000) in Cinzano et al. (1999). Ti izračuni zajemajo tudi odbito svetlobo. Po italijanskih podatkih je le majhen delež nebesnega sija posledica direktne svetlobe, večji del pa prispeva odbita svetloba, ki se ji, kot smo nakazali že prej, ne moremo izogniti, ne da bi ogrozili funkcijo razsvetljave same (Fellin et al., 2000). Končni rezultat je, da izračun krepko precenjuje energijske izgube. Ne glede na to pa so te izgube nesprejemljivo visoke! ---------------------- log I = - 4.7 – 2.5 log R + log F log I = - 4.7 + log R^-2.5 + log F log I = - 4.7 + log R^-2.5 * F log I -log R^-2.5 * F= - 4.7 log I/R^-2.5 * F= - 4.7 I= 10^- 4.7*R^-2.5 * F I= 10^- 4.7*R^-2.5 * N*Fp 10^- 4.7* Fp = 0.01, ce Fp=500 lm I = 0.01*N*R^-2.5 I = 0.00002*N*Fp*R^-2.5 10^- 4.7=0.00002 Fp je svetlobni tok na prebivalca, od 100 lm do 1000 lm, odvisno od mesta Izračun mejne magnitude JavaScript - Walkerjev zakon ================ I = 0.01Pd-2.5
Nazaj na domačo stran.