

The Earth'ís axis is tilted to its orbital plane. The gravitational pull of the Sun and the Moon on the Earth'ís equatorial bulge tend to pull it back towards the plane of the ecliptic. Since the Earth is spinning, the axis precesses. The North Celestial Pole traces out a precessional circle around the pole of the ecliptic, and at the same time the equinoxes precess backwards around the ecliptic, at the rate of 50.35 arc-seconds per year (around 26,000 years for a complete cycle).

Around 2000 years ago, the Sun was in the constellation of Aries at the spring equinox, in Cancer at the summer solstice, Libra at the autumn equinox, and Capricorn at the winter solstice. Precession means none of these is now true, but we still use the old names (e.g. the First Point of Aries for the vernal equinox), and the symbols for the vernal and autumnal equinoxes are the astrological symbol for Aries and Libra.

The Moon does not orbit exactly in the ecliptic plane, but at an inclination of about 5° to it. The Moon'ís orbit precesses rapidly, with the nodes taking 18.6 years to complete one circuit. The lunar contribution to luni-solar precession adds a short-period, small-amplitude wobble to the precessional movement of the North Celestial Pole, called nutation.
Ignoring nutation, luni-solar precession simply adds 50.35 arc-seconds per year to the ecliptic longitude of every star, leaving the ecliptic latitude unchanged.
This definition assumes the ecliptic is unchanging. In
fact, the gravitational pull of the other planets perturbs the Earth'ís
orbit and so gradually changes the plane of the ecliptic. If the equator
were kept fixed, the movement of the ecliptic would shift the equinoxes
forward along the equator by about 0.13 arc-seconds per year. This
is planetary precession, which decreases the Right Ascension of
every star by 0.13 arc-seconds per year, leaving the declination
unchanged. Combining luni-solar and planetary precessions gives general
precession.
(Lunar nutation and planetary precession also produce
slight changes in the obliquity of the ecliptic)
Because of precession, our framework of Right Ascension and declination is constantly changing. Consequently, it is necessary to state the equator and equinox of the coordinate system to which any position is referred. Certain dates (e.g. 1950.0, 2000.0) are taken as standard epochs, and used for star catalogues etc.
To observe an object on a date other than its catalogue epoch, it is necessary to correct for precession. Recall the formulae relating equatorial and ecliptic coordinates:
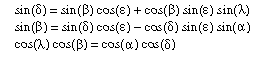
The corrections to Right Ascension and declination can be worked out by spherical trigonometry. But here we will use a different technique.

These quantities m and n are almost constant;
they are given each year in the Astronomical Almanac.
The current values are approximately:
m = 3.075 seconds of time per year
n = 1.336 seconds of time per year
= 20.043 arc-seconds per year
We can now write:
![]()
which means that, if you know the equatorial coordinates
of an object at one date, you can calculate what theyshould be at another
date, as long as the interval is not too great (20 years or so).
If the object is a star whose proper motion is known, then that should
be corrected for as well.

Alternatively, the Astronomical Almanac lists
Besselian Day Numbers throughout the year.
Take a star'ís
equatorial coordinates from a catalogue, and compute various constants
from these. Combine these with the Day Numbers for a given date, to
produce the apparent position of the star, corrected for precession,
nutation and aberration.
Return to index.