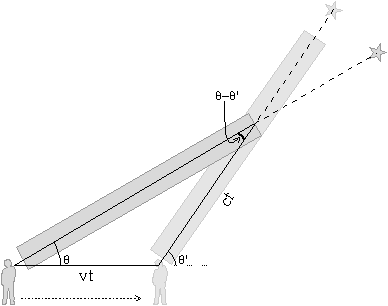
Since the Earth is moving around the Sun, stars appear to be shifted in the direction of the Earth's motion (this is analogous to raindrops falling on a person walking).

Take the Earth's velocity as v. During a time-interval t, Earth moves a distance vt, while light travels a distance ct down telescope. By plane trigonometry,
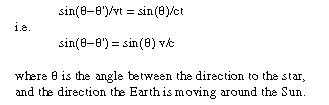
v/c is obviously very small, so we can write:
![]()
where k, the constant of aberration, is 20.5 arc-seconds.
Taking the Earth's orbit as circular, the tangent is always at right-angles to the radius. So the direction of the Earth's motion is always at 90 degrees to the direction of the Sun. Thus F, the "apex of the Earth's way", is on the ecliptic, 90 degrees behind the Sun.
The geometry is very similar to the parallax problem, with the following differences:
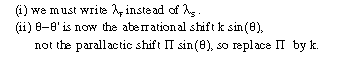

So we find:

There are two important differences between the parallactic and aberrational
ellipses:
1) The aberrational ellipse is much bigger (k is 20.5 arc-seconds, whereas
parallax is always less than 1 arc-second). Also the major axis of the
aberrational ellipse is the same for all stars, whereas the major axis
of the parallactic ellipse depends on the star's distance.
2) The phase is different. When the Sun has the same longitude as the star,
then the longitude shift is zero in the parallactic ellipse, but
the latitude shift is zero in the aberrational ellipse.
The Earth's orbit is not actually circular.
The velocity ET in any elliptical orbit can be resolved into two components:
EF constant h/p, perpendicular to
the radius vector,
EG constant eh/p, perpendicular to
the major axis of the ellipse.
It's the changing angle between these which causes the orbital velocity
to vary (Kepler's Second Law).
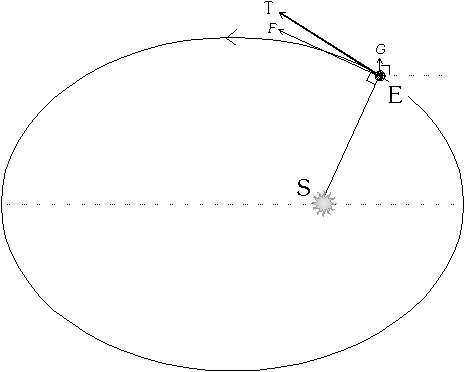
Here, EF is the velocity for a circular orbit, as assumed above. EG adds second-order terms, 0.3 arc-seconds or less, which are independent of Earthís position, and depend only on the starís position.
A star itself has its own proper motion across the sky, but this is always small and not usually known, so it is often ignored.
However, for objects within the solar system, the motion is usually known, and is too large to ignore. So astrometric observations of a planet have to be corrected for light-time: the time between the light leaving the planet, and being measured on Earth. The planet may move a significant distance during this time.
Annual aberration and light-time may be grouped together and called planetary aberration, in which case annual aberration alone is called stellar aberration.

Return to index.