

| Luna |
|

| Misija | Izstrelitev | Pristanek na Luni | Posadka |
|---|---|---|---|
| 11 | 16. julij 1969 | 20. julij 1969 | Neil A. Armstrong *
Michael Collins Edwin E. "Buzz" Aldrin, Jr. * |
| 12 | 14. november 1969 | 19. november 1969 | Charles "Pete" Conrad, Jr. *
Richard F. Gordon, Jr. Alan L. Bean * |
| 13 | 11. april 1970 | - - | James A. Lovell, Jr.
John L. Swigert, Jr. Fred W. Haise, Jr. |
| 14 | 31. januar 1971 | 5. februar 1971 | Alan B. Shepard, Jr. *
Stuart A. Roosa Edgar D. Mitchell * |
| 15 | 26. julij 1971 | 30. julij 1971 | David R. Scott *
Alfred M. Worden James B. Irwin * |
| 16 | 16. april 1972 | 20. april 1972 | John W. Young *
Thomas K. Mattingly II Charles M. Duke, Jr. * |
| 17 | 7. december 1972 | 11. december 1972 | Eugene A. Cernan *
Ronald B. Evans Harrison H. "Jack" Schmitt * |
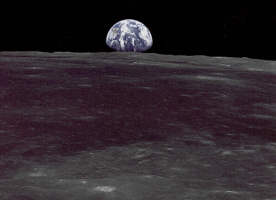




Edwin Aldrin stopa na Lunino površje, leta 1969.

Nosilna raketa projekta Apollo Saturn V.

Neil Armstrong je naredil prve korake po Luni 20. julija 1969
pozno zvečer po vzhodno ameriškem času (22:56 EDT), pri nas pa
je bil takrat že 21. julij. Neil Armstrong je izrekel znane
besede: 'To je majhen korak za človeka in velik skok za
človeštvo (That's one small step for [a] man, one giant
leap for mankind.).' Armstrongu je kmalu sledil še Edwin Aldrin.
Starost Lune
3,5 milijarde let
Polmer
1738 km
Površina
3,796×10E7 km
Prostornina
2,199×10E10 km2
Masa
7,35×10E22 kg
Povprečna gostota
3,34 kg/dm3
Gravitacijski pospešek na površju
1,61 m/s2
Srednja oddaljenost od Zemlje
384400 km
Povprečna hitrost na tiru
1,02 km/s
Druga kozmična hitrost
2,4 km/s
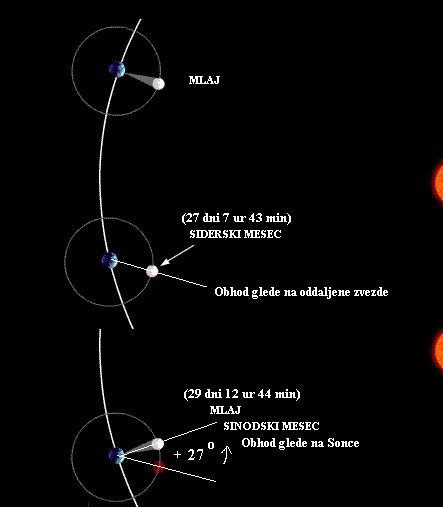
Siderski mesec (obhod okrog Zemlje glede na zvezde) - 27.212220 dni (27 dni 7 ur 43 min)
Sinodski mesec (obhod okrog Zemlje glede na Sonce) - 29.5330589 dni (29 dni 12 ur 44 min)
Kot med ekliptiko in ravnino gibanja Lune - 5 stopinj
Perigej (prizemlje) - približno 363 000 km
Apogej (odzemlje) - približno 406 000 km
Zorni kot
- Srednji zorni kot - 31'6"
- Največji zorni kot - 33'31"
- Najmanjši zorni kot - 29'22"
Dnevni zamik vzhoda Lune - približno 50 minut (odvisno od deklinacije)
Lunin dan - čas med dvema zaporednima prehodoma čez ničelni meridian
(je približno za 50,5 minut daljši od Sončevega dneva, Lunin dan se spreminja,
ker Luna potuje po elipsi).
Obrat Lune okrog lastne osi in obhod okrog Zemlje traja 28,53 Luninih dni
(to je za dan manj kot je sinodski mesec, 24h*29.53/28.53 = 24h 50.5minut)
Med nočjo in dnem je na Luni precejšnja temperaturna razlika, ponoči temperatura
na ekvatorju pade do -180°C, podnevi pa se povzpne do +100°C. Noč traja na Luni približno
15 dni!!!!!
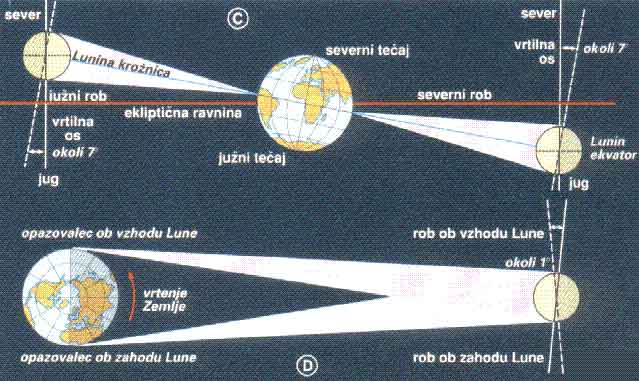
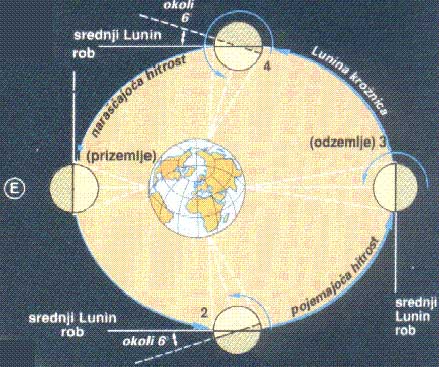
Libracija Lune
Libracija po širini znaša okrog 7 stopinj in je posledica tega,
da Lunina os vrtenja ni pravokotna na ravnino kroženja okrog Zemlje.
Os Lune je nagnjena za 6 stopinj in 40 sekund glede na os
ravnine gibanja okrog Zemlje.
Tako včasih vidimo prek Luninega severnega pola, ko je na nasprotni
strani Zemlje pa malo čez južni pol. Najmanj izrazita pa je dnevna
libracija, ki znaša 1 stopinjo in nastane zato, ker lahko
zaradi vrtenja Zemlje okrog svoje osi v eni noči Luno opazujemo
iz različnih leg.
Libracija po dolžini znaša 6 stopinj in nastane zato,
ker je Lunin tir kroženja okrog Zemlje eliptičen.
Če seštejemo vse možne površine, ki se nam kažejo ob
različnih časih, vidimo skupaj 59 % Lune
(glej tudi: http://www.kvarkadabra.net/index.html?/vprasanja/teksti/vrtenje_lune.htm
,
http://hpd.botanic.hr/ast/praktik/planeti/viskrmj/viskrmj.htm).

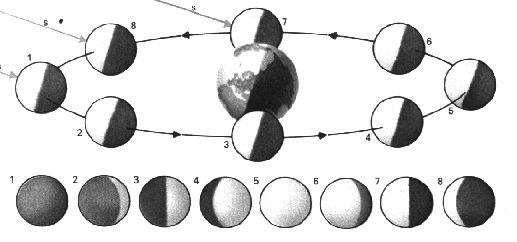
 Oglejte si tudi prostorsko sliko in
Oglejte si tudi prostorsko sliko in  nastanek luninih faz (men)
nastanek luninih faz (men)

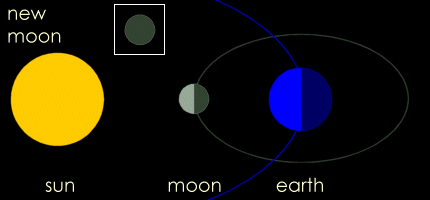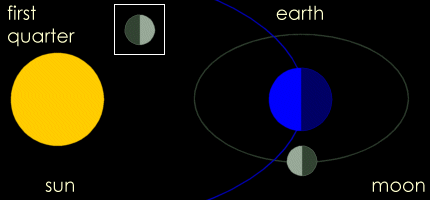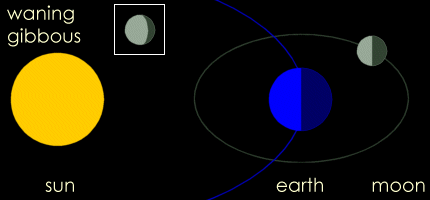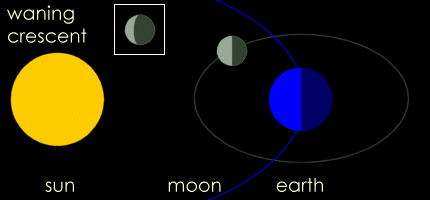

Tukaj se kaže poslužiti plesa urnih kazalcev, saj poznate pesmico: "Dolgi Luka, kratki Miha, čudna dva možica, noč in dan po eni nogi v krogu se vrtita (lovita) ...". Najprej rešimo problem, kdaj se bodo lege treh teles spet ponovile (kazalca spet srečala). Po analogiji dohitevanja počasnejšega avta, kjer je čas srečanja od trenutka, ko sta premikajoča avtomobila na radalji x, enak t = x/(Vhiter-Vpočasen), je tudi pri kroženju zgodba zelo podobna. V tem primeru je bolje uporabiti kotno hitrost (za enakomerno kroženje velja, da je kotna hitrost w kar polni kot 2*p (360o) deljen z obhodnim časom To, (w = 2*p/To ). Kotna hitrost urnega kazalca je (wu= 2*p/Tu = 2*p/12h, minutnega pa wm = 2*p/Tm = 2*p/1h. Recimo, da začnemo opazovati, ko sta kazalca poravnana skupaj (zagotovo vemo, da sta ob 12:00), potem lahko rečemo, da je razdalja med njima cel obseg, izraženo v kotu je to 2*p.
T (čas) ponovnega srečanja se torej izrazi na naslednji način:
T = kotna_razdalja/(wm - wu) = 2*p/ (wm - wu) = 1/(1/Tm - 1/Tu).
Iz povedanega sledi poučna zveza, ki povezuje obhodna časa (Tm, Tu) obeh kazalcev in čas T, ki preteče med dvema zaporednima srečanjima:
1/T = 1/Tm -1/Tu
T = Tm*Tu/(Tu-Tm) = 12/11 h
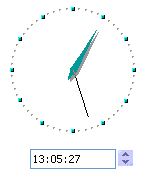
Preverite, če opazujemo prvo srečanje obeh kazalcev po 12. uri, je to
približno 5 min in 27 s čez 13. uro.
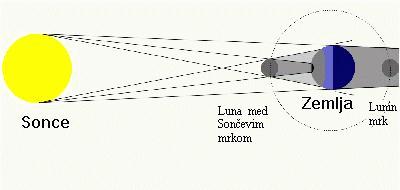
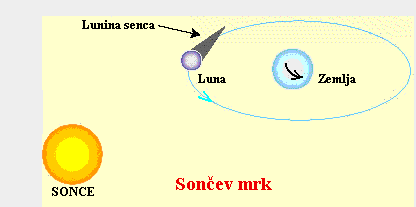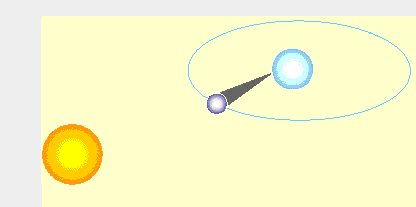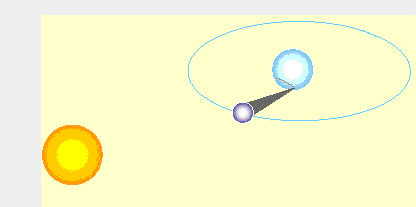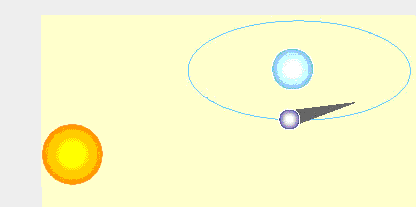
Ponovimo zgodbo pri legi Lune, Zemlje, oddaljenih zvezd in Sonca ob ponovitvi mrka.
1/tey=1/tsid - 1/tsin (ponovitev lege Zemlje, Lune glede na oddaljene zvezde)
1/tsar=1/tey -1/leto = 1/tsid - 1/tsin - 1/leto (približna ocena[!], brez upoštevanja precesije Lunine orbite)
tey = 346.6 dni (zamračitveno leto, eclipse year)
tsar= 18 let in še nekaj dni
Saros pa je za dan krajsi (18 let 10 dni 8 ur), ce je v sarosu 5 prestopnih let.
Zaradi zamika 8 ur, se mrk v naslednjem ciklu zgodi 120 stopinj zahodno in
8 ur pozneje. Po treh sarosih, približno 54 let in en mesec, se mrk zgodi blizu
'izhodiščne' lege (3*120 = 360 stopinj). Če je bil Lunin mrk zvečer
9. 1. 2001 (maks, ob 21:21 UTC), se bo
zjutraj 21.1. leta 2019 ponovil (maks, ob 6:12 UTC).
Mrk 31.1. 2037 pa se ne bo videl (maks. ob 17:01 UTC), ker je Luna še pod
horizontom. Mrk 11.2.2055 pa bo v večji meri v prvi polovici noči (maks. ob 23:45 UTC),
podobno kot 9.1.2001.
 |










Za astronomski krožek: ZORKO Vičar
Komentarji so zaželjeni.
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si