Lunin mrk posnet z 200 mm-skim objektivom. Čas osvetlitve: 1 s; Kodak 200 ISO. Luna je prehajala iz Zemljine polsence v senco. Posnetek je 21. januarja 2000 naredil Peter Mihor.

Aristotel je že okoli leta 330 pred našim štetjem trdil, da je Zemlja okrogla, ker ima Zemljina senca ob Luninih mrkih okrogel obris.

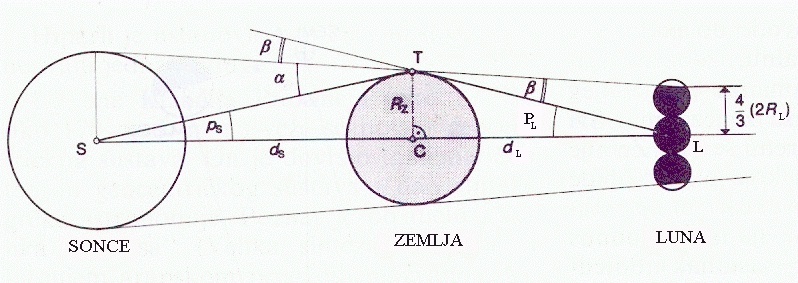
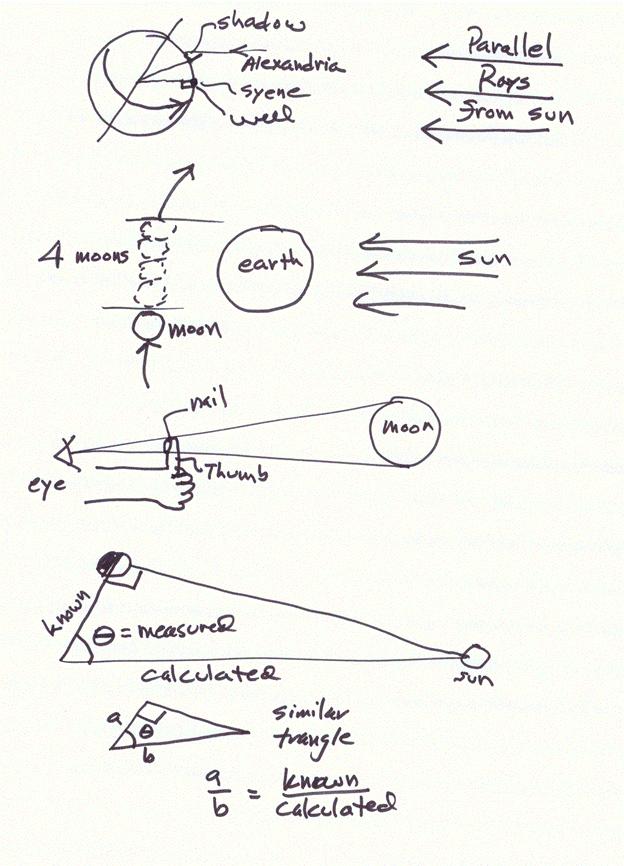
Če zraven Lune narišemo krog, ki v razmerju ustreza dimenziji Zemlje (Rz/Rl=3,7), potem opazimo, da se ukrivljenost Zemlje po pričakovanjih kar dobro ujema s senco Zemlje na Luni. Seveda je potrebno upoštevati, da senca Zemlje nima čisto enakih dimenzij kot sam planet Zemlja, in da ukrivljenost sence na okrogli Luni ni enaka kot na ravni ploskvi. To je le groba ocena razmerij. Nekoliko natančneje in z boljšo metodo sta razmerje Zemlja-Luna določila že v antični Grčiji Aristarh (živel je okoli leta 270 pr. n. š) in kasneje Hiparh. Poglejmo Hiparhov premislek. Hiparh je ugotovil, da v Zemljino senco lahko postavimo približno 8/3 Lun (Luninih premerov). Kako je to ugotovil? Luna se med zvezdami giblje s kotno hitrostjo približno 0.5 ločne stopinje na uro (30'). Hiparh je tudi izmeril, da Luna potuje čez sredino Zemljine sence od začetka vhoda v senco pa do začetka izhoda iz sence 8/3h. Če privzamemo za kotni premer Lune 30', [ (8/3)*30' = 80' ] potem je kotni premer Zemljine sence 2β=80' in je razmerje med kotoma Zemljine sence in Lune 80'/30'=8/3. To pa ni vse. V antiki so že poznali polmer Zemlje, ki ga je določil Eratosten s pomočjo razdalje med Aleksandrijo in Sieno (Asuanom) in vpadnih kotov Sončnih žarkov. V Sieni je bil ta kot 0 stopinj glede na navpičnico, v Aleksandriji pa 7,2 stopinje. Do te nadvse pronicljive rešitve je prišel, ko je izvedel, da namreč na določen dan v Sieni padajo žarki v studenec navpično (Sonce je v zenitu), torej ne delajo sence. Vrnimo se k mrku. Če bi torej poznali kot (2Pl) pod katerim bi videli Zemljo z Lune, bi lahko izračunali razdaljo med telesoma in polmer Lune. To je naredil Hiparh. Če pogledamo spodnjo sliko, lahko iz nje razberemo, da med koti α, β, Ps in Pl velja zveza: α+β=Ps+Pl.

Kot β je 40' (določen je s pomočjo trajanja mrka), α pa je približno kar enak polovici zornega kota Sonca (15'). Danes vemo, da je kot Ps precej manjši od vsote α+β, saj je premer Sonca približno 109 krat večji od Zemljinega, hkrati pa je Sonce zelo daleč glede na razdaljo Zemlja-Luna. Hiparh tega sicer ni mogel verodostojno dokazati (pri računu astronomske enote - razdalja Zemlja, Sonce - se je pojavila velika napaka), a njegova domneva o velikosti kota Ps je bila pravilna. Ker je torej kot Ps zelo majhen ( Ps << α+β) v primerjavi z α+β, ga lahko zanemarimo, končni izraz za Pl =α+β=55'.

Ker so koti majhni, velja: dl=Rz/Pl.
Kot Pl=55' moramo podati v radianih; rezultat je, razdalja Zemlja-Luna dl=62Rz.

Rezultat je presenetljivo točen. Zaradi majhnih kotov velja tudi razmerje: Rz/(4/3(2Rl))=Pl/β, in končno dobimo za razmerje med polmerom Zemlje in Lune vrednost: Rz/Rl=11/3=3,7.

Podatki za antiko in današnji podatki:
Antika                Današnja vrednost
Rz=6247 km            Rz=6378 km
Rl=3/11Rz=1700 km     Rl=1738 km
dl=62*Rz=387000 km    dl=384400 km (razdalja med Luno in Zemljo)

V antiki so torej preko Luninih mrkov dokaj dobro poznali (izračunali) podatke o dimenzijah med Zemljo in Luno, podatki o Soncu pa so bili nekoliko slabše ocenjeni (razen Eratosten bi se naj zelo približal pravilni vrednosti). To so bile tako rekoč prve ocene o tem, kako daleč so pravzaprav vesoljska telesa.

Zorko Vičar

POVZETEK:

Polmer Zemlje, je določil Eratosten s pomočjo razdalje med Aleksandrijo in Sieno (Asuanom) in vpadnih kotov Sončnih žarkov.

---

Dodatek, vir 1:
http://www.physics.unlv.edu/~lenz/PHYS%20120.S09/history.htm
Aristarchus had used the following geometrical argument to deduce the ratio of the distance of the moon from earth to the distance of sun from earth. He did this by noting that when half the moon was lit by light from the sun, the earth, moon, sun system formed a right triangle. He measured the angle between Earth and Sun and got 87° (the actual angle is closer to 89.85°) and deduced that the sun was 20 times further from earth than the moon. The actual value is about 400 times further or 80,000,000 miles.
Once the distance between earth and moon were known, it was easy to estimate the diameter of the sun since during a solar eclipse, the moon’s apparent size is just about the same as the apparent size of the sun, that is they subtend the same angle in the sky. Therefore the ratio of (moon’s diameter)/(sun’s diameter) = (distance between earth-moon)/(distance between earth-sun).

---

Vir 2: http://www.astro.umontreal.ca/~paulchar/grps/histoire/newsite/sp/great_moments_e.html
ca. 250 BC: The distance to the Sun The first mathematically-based attempt at determining the Sun-Earth distance is due to Aristarchus of Samos (ca. 310-230 BC). The procedure followed by Aristarchus is illustrated on the diagram below; form a triangle by connecting the Earth (E), Sun (S) and Moon (M). At the first or third Moon quarter, the triangle so described in a right-angle triangle (a=90°). The angle b can be measured by an observer on Earth, which then allows the angle c to be computed (c=90-b when a=90°). The ratio of the Earth-Moon segment (EM) to the Earth-Sun segment (ES) is by definition equal to sin(c) (in modern trigonometric parlance; Aristarchus expressed this differently).

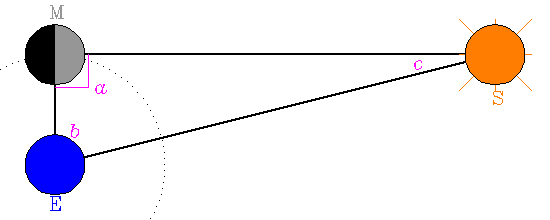
Aristarchus' geometric construction used to estimate the distance to the Sun. The Earth-Sun-Moon triangle and sizes are not drawn to scale.
While sound in theory, in practice this procedure is highly inaccurate in the Earth/Sun/Moon case; this is because EM is much smaller than ES, implying that b is very close to 90°, so that c is in turn very small. This has the consequence that a small measurement error on b translates in a large variation in the ratio EM/ES (again in modern parlance, a measurement error db is amplified by a factor 1/(sin c)^2, which is large when c is very small). Aristarchus measured b=87°, while the true value is in fact 89° 50 minutes. This may seem a small error, but because of the large error amplification Aristarchus' value leads to EM/ES=19, instead of the true value EM/ES=397. Nonetheless, Aristarchus' calculation was the first to mathematically set the spatial scale of the cosmos.

---