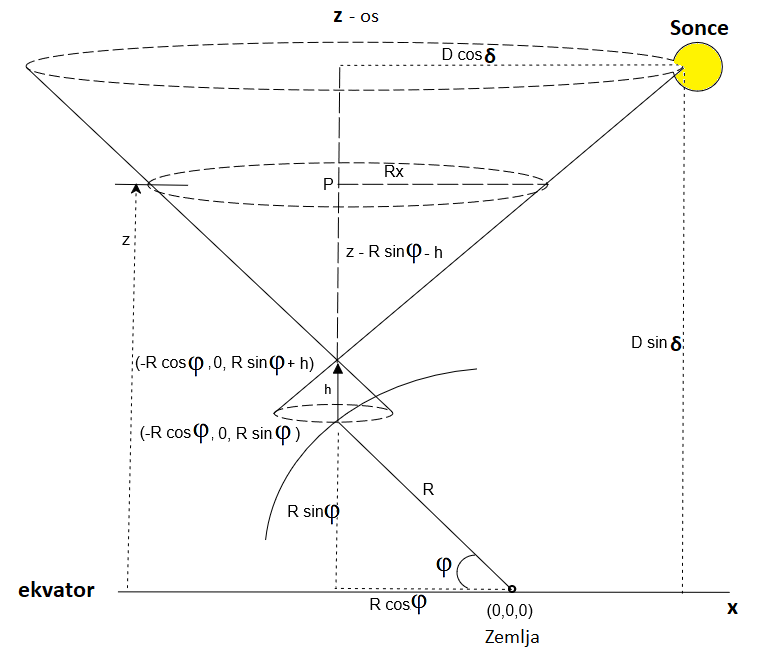
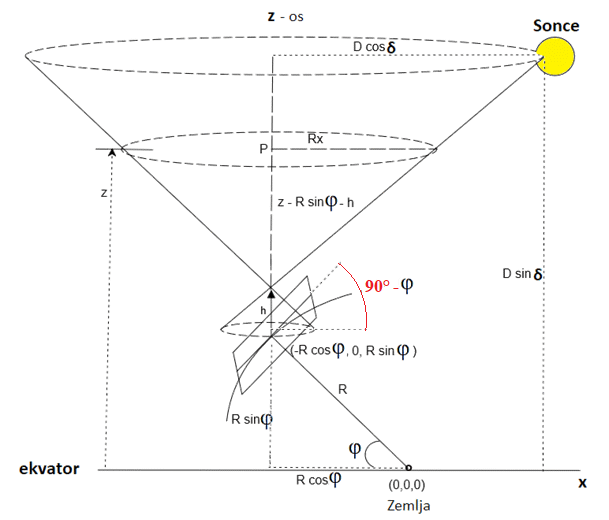
Pot sence palice zaradi navideznega gibanja Sonca po nebu (pot do gregorijanskega koledarja)

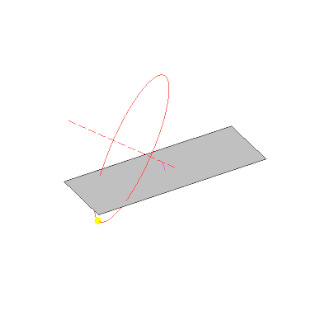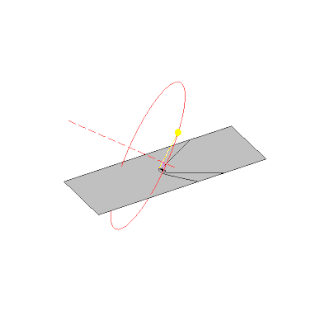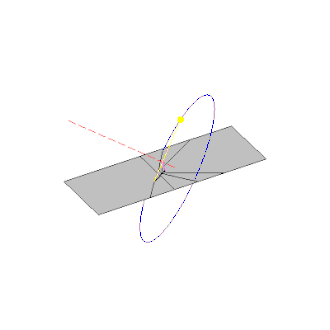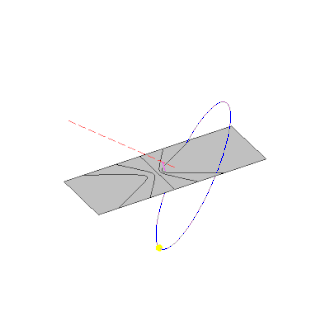
Pot sence palice zaradi navideznega gibanja Sonca po nebu. Katere informacije lahko dobimo glede na pot sence, ki jo tvori palica? Opazimo, da se senca (po vsaki označitvi vrha sence) premakne za neenakomerne kote in dolžine glede na časovne intervale. Pot sence konice pokončne palice (ali konice poljubnega ozkega telesa z višino 'v' nad vodoravno površino) je kar enaka stožčastemu preseku (hiperboli). Zakaj?
Ker je pot sence palice stožec, bo presek tega stožca z ravnino horizonta, ki oklepa kot φ (geografska širina kraja opazovanja) z osjo stožca kar stožnica - izkaže se, da hiperbola (razen na polih, kjer je krog ali elipsa nad ge. širino 90 ° - δ). Glejte slike in izpeljave, ki sledijo.

Sledi daljša matematična obravnava problema

Preprost primer palice na severnem polu.

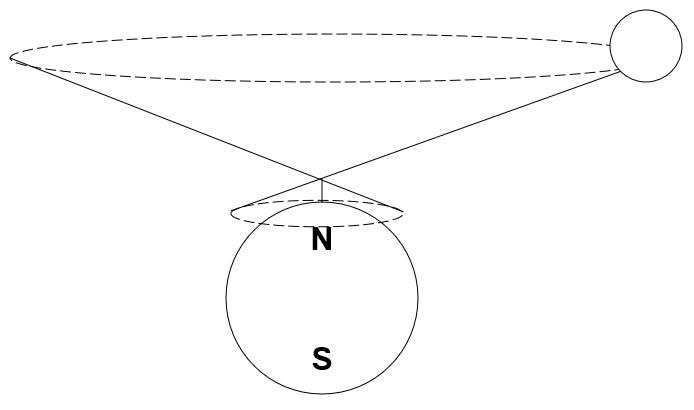
Sončna ura 1

Razmislimo o palici na severnem polu. Ko se Sonce giblje po nebesni sferi, v enem dnevu žarki, ki zadenejo konico palice oblikujejo stožec (kot je prikazano na zgornjem diagramu). Sečišče tega stožca z ravnino obzorja (palica kaže proti severu) je pot sence palice ( presečišče ravnine s stožcem je stožnica - krog, elipsa, parabola ali hiperbola). Oboroženi s temi spoznanji - ko sončni žarki čez dan tvorijo stožec z vrhom na konici palice (palica je poravnana z osjo zemeljske rotacije) in presečišče tega stožca z ravnino obzorja je kar iskana pot, ki jo začrta senca palice - potem lahko problem načeloma geometrijsko zelo enostavno rešimo.
**Nebesna sfera je namišljena sfera, ki se razteza od središča Zemlje, na kateri se zdi, da Sonce in zvezde krožijo okoli Zemlje - okoli osi rotacije Zemlje (premikanje teles na nebesni sferi je torej večinoma posledica rotacije Zemlje). Za nas kot opazovalce, ki se vrtimo skupaj z Zemljo, se zdi, da se Sonce (in zvezde) vrtijo okoli zemeljske osi v nasprotni smeri rotacije Zemlje.

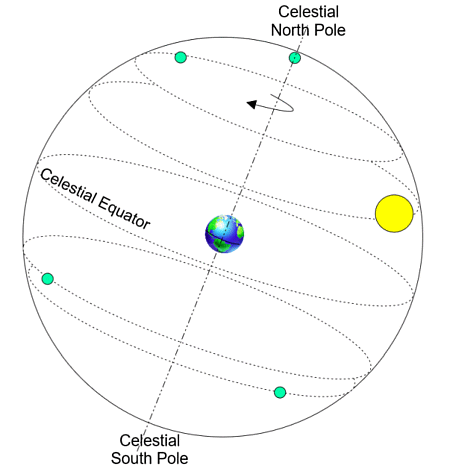
NEBESNA SFERA

2. Zdaj pa razmislimo o bolj splošnem primeru.

Preučimo palico višine 'h', usmerjeno vzdolž (vzporedno) Zemljine rotacijske osi (na severni polobli bo taka palica, ki kaže proti severu, ležala kar v osi rotacije) na zemljepisni širini 'φ' (podrobnosti o zemljepisni širini najdemo na: leto in Zemljina orbita ter s tem povezana gibanja na nebu).

Sončna ura 2

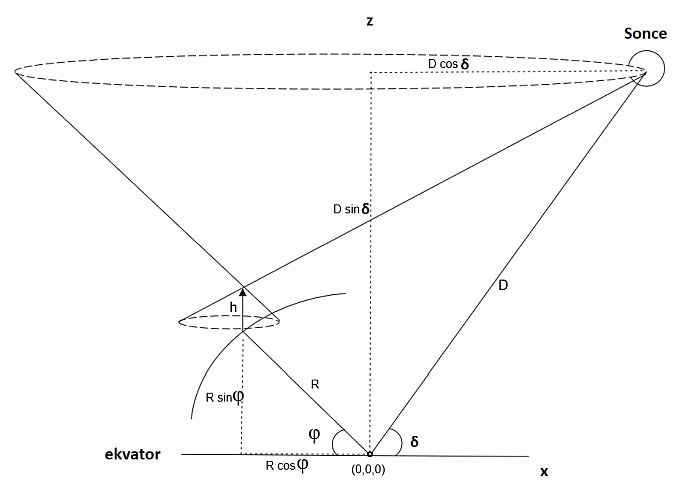
D je razdalja od središča Zemlje do Sonca in "δ" je deklinacija Sonca.

Deklinacija Sonca je analogna zemljepisni širini. Določa položaj Sonca na nebesni sferi. Natančneje določa, kako daleč na severu ali jugu se nahaja ravnina gibanja Sonca glede na nebesni ekvator. Tako kot zemljepisna širina pove, kako daleč severno, oz. južno, leži nek kraj od zemeljskega ekvatorja (gre za kotno razdaljo). Za razumevanje deklinacije Sonca, si oglejte spodnjo sliko, ki prikazuje začrtano pot Sonca na nebesni sferi skozi vse leto. To pot pa imenujemo 'EKLIPTIKA' (je v resnici ravnina orbite Zemlje okoli Sonca - skupnega težišča). Ker je os vrtenja Zemlje nagnjena za 23,44 stopinje glede na orbito Zemlje okoli Sonca (podatki so različni), zato Sonce v različnih letnih časih leži na različnih položajih nebesne krogle.

Sončna ura 3

Primerjava koordinatnega sistema na Zemlji in na nebesni krogli.

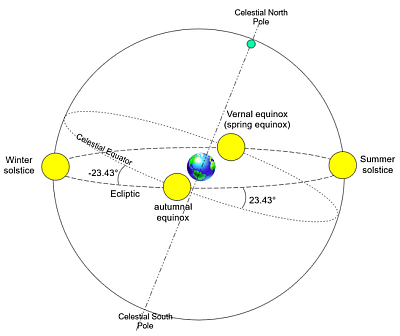
Poudarimo še: na poletni solsticij je os Zemlje najbolj nagnjena proti Soncu: deklinacija Sonca je takrat 23,43°. Simetrično je ob zimskem solsticiju, ko je zemeljska os nagnjena stran od Sonca in je deklinacija Sonca: -23,43 °. Ob enakonočju zemeljska os ni nagnjena ne stran, ne proti Soncu, deklinacija Sonca je takrat: 0 °. Zato deklinacija Sonca skozi vse leto niha od 23,43° do -23,43°.

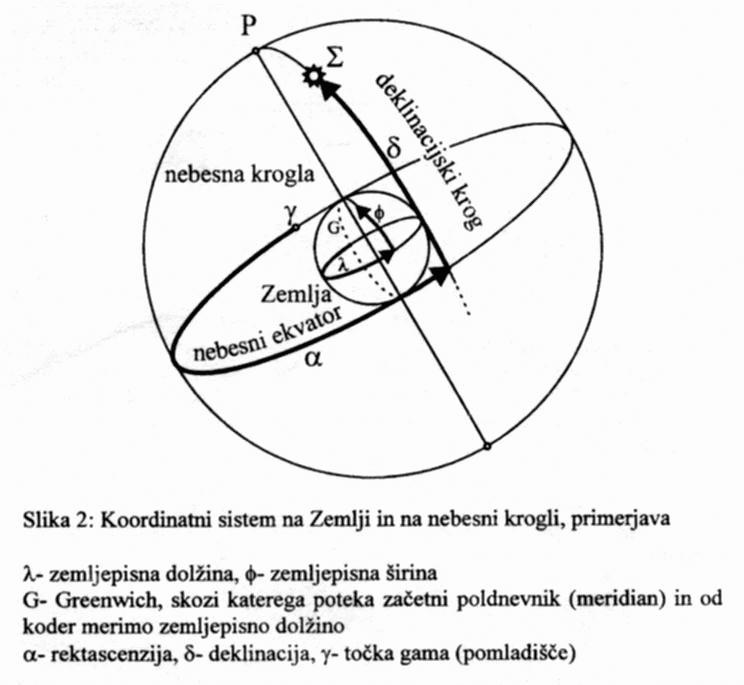
Če se vrnemo k problemu, se jasno vidi, da se Sonce navidezno premika po krogu s polmerom D cosδ in središče tega kroga leži na višini D sinδ od središča Zemlje.

Iz prejšnje slike je razvidno, da je središče kroga Sončnega gibanja zamaknjeno za Rcosφ od konico palice. Ker je polmer tega kroga Dcosδ >>> Rcosφ (D = razdalja Sonca od Zemlje, 149,6 milijona km in R = polmer Zemlja, 6371 km), lahko štejemo, da središče gibanja Sonca poteka vzdolž konice palice, kot je prikazano na sliki spodaj:

Sončna ura 4

Zdaj moramo najti enačbo stožca, ki ga tvorijo Sončni žarki na konici palice v obhodu enega dneva (slika levo). Koordinate (0, 0, 0) so v središču Zemlje.
Povejmo še, da je ravnina pod palico kar ravnina našega obzorja, ki se dotika Zemlje na vbodišču palice (slika desno). Torej črta, ki povezuje središče Zemlje in točko preboda palice s tlemi, je kar normalna na to ravnino. Iz tega je mogoče najti enotski vektor, ki je kar normala na ravnino [ n = r/|r| = (-R cosφ, 0, R sinφ)/R = (-cosφ, 0, sinφ) ]. Poleg tega ta ravnina poteka skozi koordinate vboda palice r_o = (-R cosφ, 0, R sinφ ), y os kaže v ravnino. Pozneje bomo to ravnino našega obzorja obravnavali posebej in na njej poiskali presek s stožcem sence palice.

Obravnavajmo točko P na višini 'z' od središča Zemlje. Koordinate takšne točke so (-Rcosφ, 0, z). Polmer kroga osnovne ploskve stožca na tej višini je 'Rx' v središčni točki P z že omenjenimi koordinatami (-Rcosφ, 0, z). Tako je enačba kroga osnovne površine podana kot:

(x+Rcosφ)² + y² = Rx²

Sončna ura 5

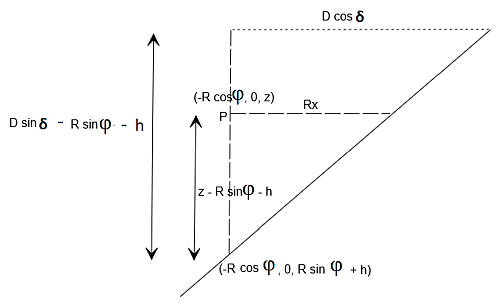
Zdaj bomo poiskali izraz za "Rx". Na zgornji sliki obravnavajmo manjši pravokotni trikotnik z osnovo 'Rx' in višino ‘z – R sinφ – h’ in podobno (večji) trikotnik z osnovo 'D cosδ' in višino 'D sinδ – R sinφ – h’. Iz podobnih trikotnikov veljajo naslednja razmerja:

Rx/(Dcosδ) = (z-R sinφ-h)/(Dsinδ-Rsinφ-h)

Rx/(Dcosδ) = (z-R sinφ-h)/(D(sinδ- Rsinφ/D-h/D))

Ker je D >> R in tudi D >>> h, velja:

Rx = cosδ(z - R sinφ-h)/sinδ

Rx = (z - Rsinφ - h)/tanδ

Enačba stožca (osnovne površine, preseka z ravnino) ima sedaj obliko:

((x+Rcosφ)² + y²)tanδ² = (z-R sinφ-h)²

To je enačba stožca, oblikovanega na konici palice višine 'h', ki je usmerjen vzdolž zemeljske osi vrtenje. Zagotovo velja, če ravnina obzorja (ki poteka skozi osnovo palice) preseka stožec, bo senca sledila stožcu - stožnici. Ta stožčasti prerez je torej pot, ki jo zariše senca palice. Spodnja slika prikazuje ravnino obzorja in stožec, ki ga nariše senca palice na horizontalni ravnini.

Sončna ura 6

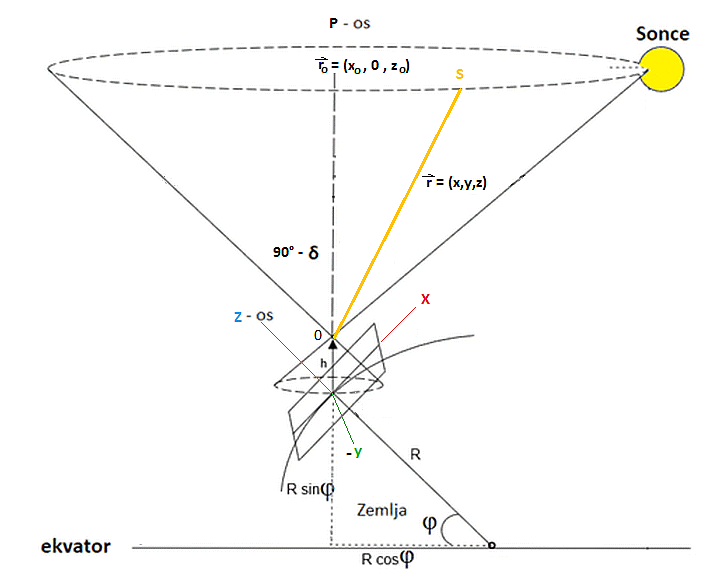
Ker je pot sence palice stožec, bo presek z ravnino horizonta, ki oklepa kot φ z osjo stožca, kar stožnica - izkaže se, da za naše kraje kar hiperbola (zmerne geografske širine, v bližini polov to ne velja).
Povejmo še, da se je v Sloveniji veliko s sencami Sonca ukvarjal spoštovani prof. Marijan Prosen.
Iz zgornje slike preidimo na spodnjo, kjer obravnavamo zgolj horizont opazovališča (tangentno ravnino na Zemljo), koordinatni sistem bo postavljen v vrh stožca (velja za sliki spodaj).

Kako pa je torej s potjo sence vertikalne palice glede na uro in dan v letu na horizonzalni ravnini. Deklinacija Sonca se spreminja od -23,44° do +23,44° (glede na nebesni ekvator, ki je preslikava zemeljskega na nebesno sfero).

V ta namen pa si na hitro še poglejmo, kako elegantno lahko z vektorji in skalarnim produktom opišemo stožec, oziroma enačbo osnovne ploskve stožca ali enačbe presekov s poljubno ravnino (enačbe stožnic).

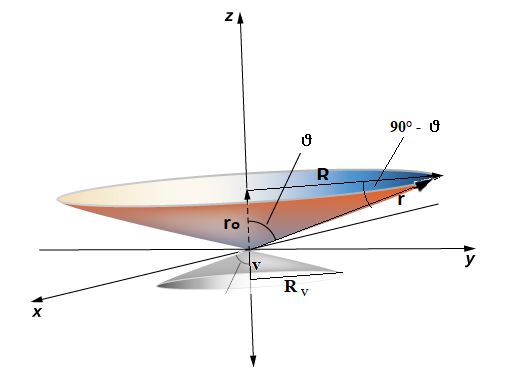
Najprej glede zapisov vektorjev in skalarjev - poudarjene oznake so vektor, nepoudarjene pa velikost vektorja, recimo r = |r|.
Večinoma nas tega ne učijo - a najlažje je stožec zapisati (enačbo preseka) v vektorski obliki in s skalarnim produktom. Pomagajmo si z zgornjo sliko, kjer velja, da je krajevni vektor r na plašču stožca kar vsota vektorjev višine ro in vektorja polmera preseka R. Velja tudi r² = x² + y² + z², v našem primeru je z = ro, tako velja r² = x² + y² + ro². Zapišimo znani povezavi mer vektorji ro, r in R, ki jih razberemo iz zgornje slike :
r = ro + R
Oziroma:
ro = r - R
Izvedimo torej skalarni produkt. Ker želimo skalarni zapis preseka stožca s polmerom R, pomnožimo (skalarno) zgornjo enačbo za ro z vektorjem r in tako dobimo višino stožca ro povezano z vektorjema r in R. Velja:
r·ro = r·r - r·R
Po definiciji skalarnega produkta velja, da je
r·ro = r·ro cos θ = ro²,
potem velja r·r = r²
in r·R = R r cos (90° - θ) = R r sin (θ ) = RR = R².
Tako dobimo znan izraz:
r·ro = r·r - r·R = r·ro cos θ ,
oziroma po poenostavitvi pričakovano velja kar Pitagorov izrek:
ro² = r² - R²
ro² = x² + y² + ro² - R²
Tako nam ostane znana enačba preseka, v tem primeru kroga, ostale stožnice izpeljemo v nadaljevanju. Torej iz zgornje enačbe sledi enačba pravokotnega preseka stožca na višino, ki je krožnica:
x² + y² = R²
Če pogledamo preslikavo pod izhodišče koordinatnega sistema, kjer ravnina kar
z = -v
in polmer R_v, potem velja:
v² = x² + y² + v² - R_v²
Presek z ravnino z = -v je torej pričakovano kar:
R_v² = x² + y²

Sledi posplošitev zgornjega razmišljanja na preseke s poljubno ravnino, recimo (x, y, ±v), ko je os stožca nagnjena glede na x os za kot φ - leži torej v ravnini (x,z). Potem bomo splošno enačbo uporabili še za gibanju sence pri navpični in poševni palici, recimo glede na horizontalno ravnino.

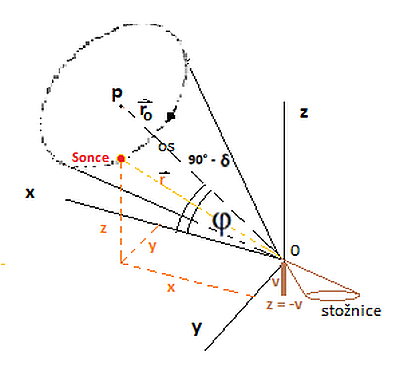
Slika zgoraj je del pred prejšnje slike tangentne ravnine na Zemlji, le da je poenostavljena za pogled z Zemlje in sedaj kar na pokončno palico višine 'v' (pravokotno na površino horizonta, torej ni več vzporedna osi vrtenja Zemlje, razen seveda na polih), katere enačbo sence iščemo. Skica prikazuje stožec, po katerem potuje Sonce (senca pokončne palice, ki pa seveda ni v merilu). S pomočjo obeh slik bomo zapisali skalarni produkt med vektorjem polarne osi (ro) (osi navideznega kroženja Sonca in ostalih nebesnih teles po nebu) in krajevnim vektorjem (r) od vrha stožca do Sonca (za katerega lahko trdimo, da je za nas neskončno daleč). Kot med vektorjema je kar (90° - δ). Iz slike opazimo, da vektor osi stožca (ro) leži v ravnini sever - jug (določa jo krajevni meridian), glede na orientacijo koordinatnega sistema, je to ravnina, ki jo tvorita (z) in (x) koordinati.
Skalarni produkt (r·ro) nam bo, kot bomo videli, dal kar splošno enačbo stožca, preseka z ravnino v prostoru.
Še opozorilo. Na zgornji splošni sliki (skici) je simbolično narisana (oranžna) elipsa, drugače pa so stožnice še parabola, hiperbola in krog - snov iz srednje šole.

Zapišimo torej najprej komponente vektorja r in ro:

ro = (xo, 0, zo) - ker leži v ravnini x,z

r = (x, y, z)

r² = x² + y² + z² - kvadrat velikost vektorja

Skalarni produkt bo torej po definiciji kar:

r·ro = |r|·|ro|cos(90° - δ) = |r|·|ro|sin(δ)

Sedaj zapišimo skalarni produkt r·ro še s komponentami:

r·ro = (xo, 0, zo)·(x, y, z) = x*xo + z*zo

Oba zapisa izenačimo in delimo z velikostjo vektorja osi stožca |ro|.

x*xo + z*zo = |r|·|ro|sin(δ)

Po deljenju enačbe z velikostjo (dolžino) osi stožca |ro| dobimo:

|r|·sin(δ) = x*xo/|ro| + z*zo/|ro|

Is slike razberemo, da se da razmerji zapisati kar s koti:

xo/|ro| = cos φ
zo/|ro| = sin φ

Tako lahko zapišemo splošno obliko produkta |r|·sin(δ) kar s kotnima funkcijama:

|r|·sin(δ) = x*xo/|ro| + z*zo/|ro| = x cos φ + z sin φ

Sedaj zapišimo še končno obliko enačbe preseka stožca v kvadratni obliki [ r²·sin²(δ) = (x cos φ + z sin φ)² ] :

(x² + y² + z²)sin²δ = (x cos φ + z sin φ)²

Kako pa je dejansko s presekom vodoravne ravnine? Vodoravna ravnina, na kateri opazujemo senco, je zapisana kar z enačbo:

z = -v

Kot smo že omenili, je presek s to ravnino stožnica, po kateri potuje senca konice pokončne (recimo ošiljene) palice. Da dobimo iskano enačbo stožnice za pot sence skozi dan za realno palico, vstavimo v zgornjo splošno enačbo izraz za horizontalno ravnino pod palico, ki je kar z = -v. Tako dobimo iskano enačbo prirejeno za Zemljo, palico in Sonce (z deklinacijo δ), velja pa seveda univerzalno:

(x² + y² + v²)sin²δ = (x cos φ - v sin φ)²

Zgornji zapis je torej enačba poti, stožnice, ki ji sledi senca palice višine 'v', ki je pokončno zapičena na horizontalno ravnino. To odvisnost smo tudi iskali. Enačba predstavlja torej stožčasti prerez (v našem primeru hiperbolo). Spodnja preprosta slika narejena s spletnim risalnikom 'desmos' potrjuje povedano.

Sončna ura 7

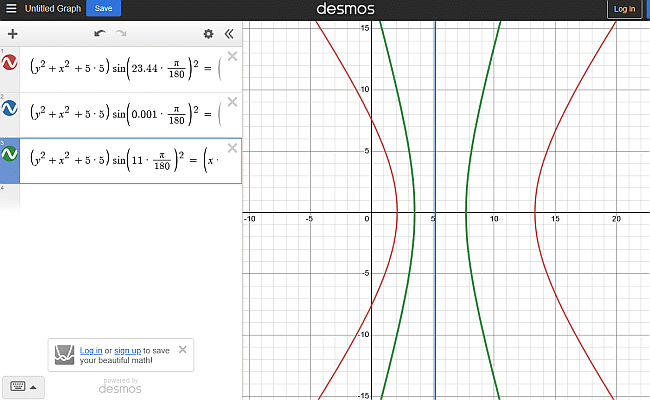
Izris poti sence (hiperbol), od leve proti desni, za φ=46° (recimo Slovenija), za deklinacije:
δ=23.43° (poletni solsticij),
δ=11° (dan med poletjem, cca 25. avg.),
δ=0° (enakonočji),
δ=-11° (dan v jeseni, cca 23. okt.),
δ=-23.43° (zimski solsticij).
Za vse dni, razen za enakonočji, je pot sence hiperbola.

Za palico na polu φ=90° bo senca sledila krožni poti in ob enakonočju (cca 22. september in cca 21. marec, ko je δ=0°, senca izriše ravno črto).

V aplikacijo 'desmos' lahko vstaviš recimo enačbo:

\left(y^{2}\ +\ x^{2\ }+5\cdot5\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -\ 5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

\left(y^{2}\ +\ x^{2\ }+5\cdot5\right)\sin\left(0.001\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -\ 5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

\left(y^{2}\ +\ x^{2\ }+5\cdot5\right)\sin\left(11\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -\ 5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

Še vaji. Testiral sem enačbo recimo za dolžino sence za 21. jun. 2025, deklinacija δ = 23.44 °, ob 16:23:00, ko je azimut Sonca 270 °, je torej na zahodu, višina Sonca pa je 33.47 °. Podatke sem dobil preko kalkulatorja lege Sonca:
http://www2.arnes.si/~gljsentvid10/visina_sonca01a.html .
Torej bi Senca morala biti dolga (pri palici višine 5 cm, pri x = 0), y = v/tan(33.47°) = 5 cm/tan(33.47°) = 7.56 cm.
Če pogledate na graf, boste dobili vrednost 7.53 (sečišče krivulje z y osjo), kar glede na približnost deklinacije dokazuje ustreznost enačbe.

Na poletni solsticij bi ob 12 h morala biti senca dolga x = v tan(φ - δ) = 5cm * tan(46 - 23.44) = 2.077 cm
- in ta vrednost tudi ustreza preseku hiperbole z x osjo.

Enake vaje lahko naredite za enakonočje in poletni solsticij.

Še alternativna izpeljava poti sence palice - ki je pa dobljena z metodo rotacije koordinatnega sistema, vsekakor zelo zanimiva izkušnja.
Obstaja pa še žal napačna izpeljava, kjer so narobe upoštevali rotacijo ravnine (kar z enačbo nove ravnine in ne s preslikavo koordinat). Njihova izpeljava da napačne krivulje, dolžine senc !!! Njihova izpeljava se začne odlično, potem pa spregledajo znano matematično resnico, da rotacija ni translacija.

Risanje sence.
Priporočam tudi 3D spletni risalnik 'desmos 3D' - https://www.desmos.com/3d [osnova za risanje stožca je recimo
y^2+(z-5)^2=f(x)^2
ali
y^2+x^2=f(z-5)^2, klikneš še na opcijo add slider [f]
ali
z=ax^2+by^2 - dovoliš add slider a b all (a in b parametra se spodaj na drsnikih privzeto nastavita na 1, lahko pa ju seveda spreminjaš)
ali
segment((3,0,0),(0,0,4)) - premica od do
ali
(0,0,5) - točka na osi z = 5 ]

Pomoč za risanje 3d grafov z orodjem desmos:
* https://docs.google.com/document/d/1jDJC0Zw7cB82SNEc04m5HGQHaXYaJK62iZM88ojNYwI/preview?tab=t.0
* https://help.desmos.com/hc/en-us/articles/19796006153997-Getting-Started-Desmos-3D
* https://blog.desmos.com/articles/beta-3d-release/

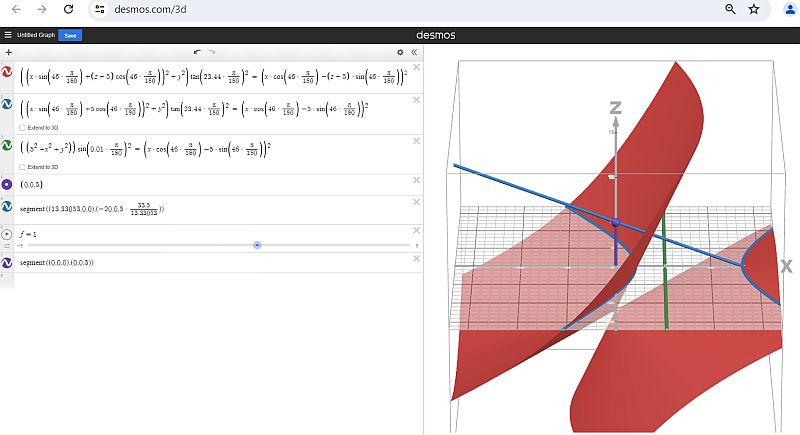
3D graf sence pokončne palice dolžine v = 5 cm. Tisto kar se lepo opazi je, da se enačba stožnice (v tem primeru hiperbole - modri krivulji), pričakovano lepo ujema s presekom stožca na ravnini (x, y). Enakonočji predstavlja zelena črta. Modra premica predstavlja Sončev žarek na vrhu palice ob zimskem solsticiju.
Za pote sence vstavite v 3d graf recimo enačbe:

* alternativna enačba stožca - izris:
\left(\ \left(x\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\ +\left(z+5\right)\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\right)\tan\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -\left(z+5\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

presek ravnine - alternativna enačba stožnice:
\left(\ \left(x\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\ +5\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\right)\tan\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

* presek ravnine - klasična enačba stožnice (enakonočje δ ≈ 0):
\left(\ \left(5^{2}\ +x^{2}\ +\ y^{2}\right)\right)\sin\left(0.01\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

* klasična enačba stožca - izris:
\left(\ \left(\ z+5\right)^{2}\ +x^{2}\ +\ y^{2}\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -\left(z+5\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

* presek ravnine - klasična enačba stožnice:
\left(\ \left(5^{2}\ +x^{2}\ +\ y^{2}\right)\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

* risanje pomožnih črt:
\left(0,0,5\right)
\operatorname{segment}((13.33053,0,0),(-20,0,5\cdot\frac{33.5}{13.33053}))
\operatorname{segment}((0,0,0),(0,0,5))

3D spletni risalnik 'desmos 3D' - https://www.desmos.com/3d .

Pelica dolžine h, ki kaže prodi osi vrenja nebesnega svoda in njena senca

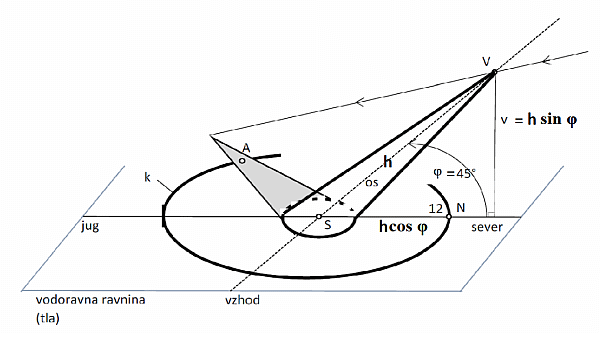
Enačba dolžine sence za palico dolžine 'h', ki kaže proti osi rotacije nebesne sfere (blizu Severnice), je torej vzporedna z osjo navideznega gibanja Sonca in oklepa z vodoravnico kot φ (to je geografska širina opazovališča, zato je višina konice nad horizontalo v = h sin φ), je:

((x - h cos φ)² + y² + (h sin φ)²)sin²δ = ((x - h cos φ) cos φ - h sin φ sin φ)²

Izhodišče koordinatnega sistema smo tudi tokrat premaknili v točko vboda palice v Zemljo, zato je x-os premaknjena za h cos φ (to je za projekcijo palice na tla, glejte sliko). Če narišemo recimo oba grafa skupaj (krivulje sta vzporedni), za vertikalno palico v = 5 cm in ustrezno palico poravnano z osjo Rotacije Zemlje h = v/sinφ = 5 cm/sin 46° = 6.95082 cm, dobimo vzporedni hiperboli. Na spodnji sliki se lepo opazi, da ko je senca usmerjena na vzhod (x = 0) za navpično palico v = 5 cm (za 21. jun. 2025, deklinacija δ = 23.44 °, ob 16:23:00, ko je azimut Sonca 270 °, višina Sonca pa je 33.47 °), senca poševne palice ni usmerjena na vzhod, rdeča krivulja, ampak ima koordinate (4.82844, 7.53346). Navpična palica, modra krivulja, pa ima koordinate (0, 7.53346). Rdeča krivulja ima za ta čas in datum dodano še koordinato zamika izhodišča v vbodišče palice [ h*cos(46°) = 6.95081795508 cm*cos(46°) = 4.82844 cm ]. Spodnja slika.

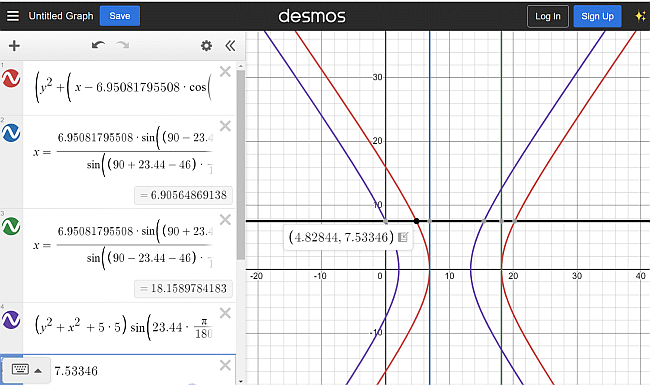
Grafa poteka senc dveh palic, vertikalne v = 5 cm (modra krivulja) in poševne (vzporedne z osjo rotacije Zemlje, kjer je h = 6.95081795508 cm in v = h sinφ = 6.95081795508 cm*sin(46°) = 5 cm, za deklinacijo &delta = 23,44 °, poletni solsticij) - rdeča krivulja. Poti senc sta lepo vzporedni, enačbi sta:
(x² + y² + v²)sin²δ = (x cos φ - v sin φ)²
((x - h cos φ)² + y² + (h sin φ)²)sin²δ = ((x - h cos φ) cos φ - h sin φ sin φ)²

Spet lahko v aplikacijo 'desmos' vstaviš spodnjo enačbo v kodni obliki (palice dolžine h = 5 cm usmerjena proti osi vrtenja nebesne krogle):
\left(\ \ \left(x-5\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\ +\ \left(5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(\left(x-5\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

- ali za vertikalno palico v = 5 cm:
\left(y^{2}\ +\ x^{2\ }+5\cdot5\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -\ 5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

Senca pri taki poševni palici (poravnani z osjo rotacije Zemlje) ne sovpada s smerjo 'vzhod - zahod' (recimo, ko sta azimut Sonca 90° ali 270°). Zato je navpična palica morebiti bolj primerna za Sončno uro, stvar okusa. Je pa poševna palica (poravnana z osjo rotacije Zemlje), na katero je pravokotno nameščena okrogla plošča (projekcija sence nanjo je kar krožnica, ker je ta ravnina vzporedna ekvatorialni), zelo primerna za merjenje časa, za številčnico, saj so ure med sabo razmaknjene za enake kote (360 °/24 h = 15 °/h) - slika in razprava spodaj. Še prej pa preverimo dolžino sence palice dožine h = 5 cm, ki je usmerjena proti nebesnemu polu, za 12. h po socu, ob dnevni kulminaciji Sonca, ob enakončjih cca 21. marec, cca 23. september, ob poletnem solsticiju cca 21. junij in zimskem solsticiju 21. decembru (v teh datumih prihaja do dnevnega zamika, večinoma zaradi necelega štvila dni v letu, tropsko ali Sončevo leto traja približno 365.242189 srednjih Sončevih dni, tako smo definirali prestopna leta - več si preberite spodaj pri koledarju). Kot bomo videli, se enačba sence lepo sklada s spodnjimi izračuni v trikotniku palica, senca, Sončev žarek.

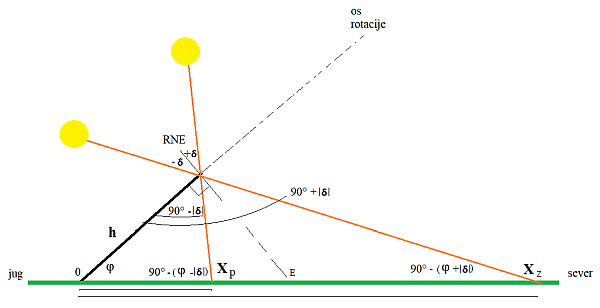
RNE - je ravnina vzporedna ekvatorski ravnini Zemlje, je pravokotna na palico. Iz slike razberemo (na njej je kot δ podan absolutno), da ob kulminacijah Sonca, za palico dolžine recimo h = 5 cm, ki je usmerjena proti nebesnemu polu (za ge. širino φ = 46 °), velja sinusni izrek za dolžino sence - glejte oznake na sliki:

Xp/sin(90° - δ) = h/sin(90° - (φ - δ))

- na poletni solsticij (ko je deklinacija δ = 23.44 °) ob kulminaciji Sonca (12 h), je tako senca dolga:
Xp = h sin(90° - δ)/sin(90° - (φ - δ)) = 5 cm sin(90 ° - 23.44 °)/sin(90° - (46 ° - 23.44 °)) = 4.96750795087 cm
- ob zimskem solsticiju (ko je deklinacija δ = -23.44 °)):
Xz = h sin(90° - δ)/sin(90° - (φ - δ)) = 5 cm sin(90 ° + 23.44 °)/sin(90° - (46 ° + 23.44 °)) = 13.0624759098 cm
- ob enakonočjih (ko je deklinacija δ = 0 °)) pa:
XE = h sin(90°)/sin(90° - φ) = 5 cm /sin(90° - 46 °) = 7.19778269813 cm

Koda za izris spodnjega grafa in izračun dolžine senc za zgornji primer (h = 5 cm, palica oklepa kot 46 ° s horizontalo - kaže proti osi vrtenja nebesne krogle):
\left(\ \ \left(x-5\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\ +\ \left(5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(\left(x-5\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}

\frac{\left(5\cdot\sin(90\cdot\frac{\pi}{180}-23.44\cdot\frac{\pi}{180})\right)}{\sin(90\cdot\frac{\pi}{180}-(46-23.44)\cdot\frac{\pi}{180})}

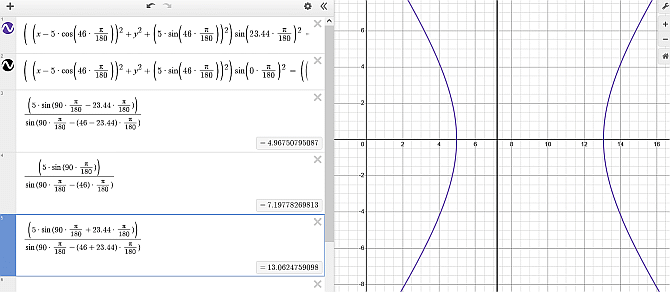
Zgornja slika je narejena s spletnim risalnikom 'desmos'. Senca palice (h = 5 cm, palica oklepa kot 46 ° s horizontalo - kaže proti osi vrtenja nebesne krogle) - dnevni potek med poletnim in zimskim solsticijem ter enakonočjema.

3. Merjenje časa s Sončno uro

Spomnimo se, kako senca palice na severnem tečaju sledi krožni poti na vodoravni ravnini. Ravnina obzorja na severnem polu je vzporedna z ekvatorjem. Na kateri koli zemljepisni širini 'φ', če palico poravnamo vzdolž zemeljske osi (tj kaže proti severu in tvori kot z vodoravno ravnino, ki je enak zemljepisni širini) in sledimo senci na vzporedni ravnini z ekvatorjem (takšna ravnina bo pravokotna na palico) potem bomo videli, da senca sledi popolnoma krožni poti. To je koncept ekvatorialnih Sončnih ur.

Sončna ura 8

Ekvatorialna Sončna ura pri pomorščakovem spomeniku, Port Arthur, Teksas, ZDA (geografska širina 29°52). Palica oklepa kot 29°52 z vodoravnico in kaže proti severu

Slika je vzeta iz: http://www.wsanford.com/~wsanford/exo/sundials/stpete/

Palica se imenuje tudi "gnomon". Z vodoravno ravnino oklepa kot enak lokalni zemljepisni širini in je usmerjena proti pravemu severu.

Zemlja se zavrti okoli svoje osi glede na Sonce v 24 urah, torej ima kotno hitrost 360°/24 h [stopinj na uro] oz. 15° na uro. Za nas opazovalce, ki rotiramo vzdolž Zemlje, se zdi, da se Sonce po nebu giblje s kotno hitrostjo 15° na uro. Z drugimi besedami, Sonce se premakne za 15° v 1 uri na nebu. To pomeni, da se bo senca na ekvatorialni številčnici (kot je zgoraj) premaknila za 15° v eni uri.

Na podlagi tega preprostega sklepanja so črte, ki označujejo ure, tudi narisane na ekvatorialni številčnici. Toda ena uganka še vedno ostaja in to je: kako oštevilčiti te ure, kako bi vedeli, če je 6 popoldan ali ob 16 h ?

To težavo je mogoče rešiti z zavedanjem, da je opoldne za dani kraj na Zemlji Sonce neposredno nad glavo (natančneje, je na začetnem poldnevniku, na velikem krogu, ki poteka skozi kraj/točko na Zemlji ter nebesni severni in južni pol). Tako bo senca palice, usmerjene proti severu, opoldne kazala proti sever. Zato so lahko urne črte na ekvatorialni Sončni uri označeno kot je prikazano na sliki:

Sončna ura 9

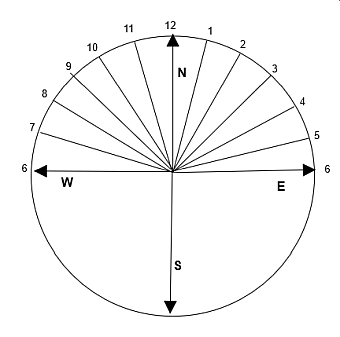
Črta, linija, ki kaže proti severu, se zgodi opoldne (12.00).

Ekvatorialne Sončne ure morajo biti označene na obeh straneh, saj pozimi na eni strani ne bo nastala senca. To je zato, ker gre Sonce južno od nebesnega ekvatorja (ali, ker Sončna deklinacija postane negativno po enakonočju). Ugotovimo lahko, da so ekvatorialne Sončne ure lahko razumljive, vendar jih je praktično težko narediti.

3.1 Horizontalne Sončne ure

V tej vrsti konfiguracije je palični "gnomon" podoben ekvatorialni Sončni uri, usmerjen proti severu in tvori kot, ki je enak lokalni zemljepisni širini z vodoravna ravnina. V tej konfiguraciji se senci sledi na vodoravni ravnini.

Trik tukaj je najti urne črte. Da bi poiščite urne premice si lahko predstavljamo ekvatorialno Sončno uro z urnim kotom ‘E’= 15° (kot med dvema urnima črtama) in projiciramo krožnico ravnina te številčnice na vodoravni ravnini ob ‘gnomonu’ oz palici.

Sončna ura 10

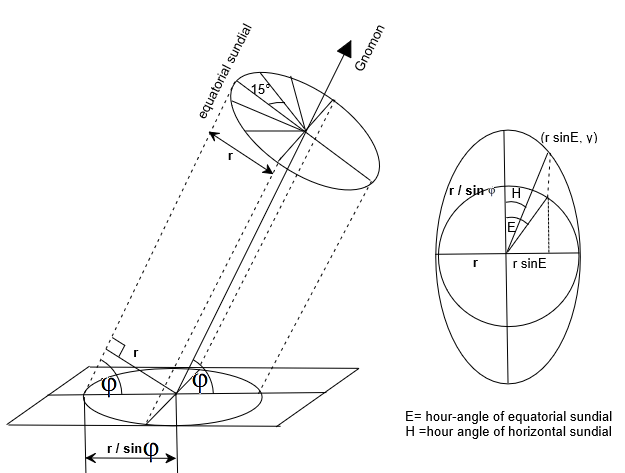
Projekcija kroga na vodoravno ravnino je elipsa (lahko se dokaže). Zapišimo enačbo elipse:

x²/a² + y²/b² = 1

Kot izjemo, v tej orientaciji elipse zamenjamo pomen konstant a in b, naj bo torej v tem primeru b glavna os elipse in a mala - zgolj za naš primer. Naj bo polmer številčnice "ekvatorialne Sončne ure" 'r'. Iz slike (levo) razberemo, da je mala os 'a' = r in glavna os elipse oklepa kot φ s polmerom 'r' in zato velja:

b = r/sinφ

- zadnji izraz nadomestimo v enačbi elipse:

x²/r² + (y²/r²)sinφ² = 1

Na sliki zgoraj desno je urna črta na ekvatorialni številčnici pod kotom od V (=15°) do črte sever-jug (ali črte opoldanske ure). Koordinate ustrezne projekcije urnega kazalca na elipso lahko dobimo kot: (r sinE, y). Zamenjava v enačbi elipse:

(r² sinE²)/r² + (y²/r²)sinφ² = 1

Rešitev zgornje enačbe za spremenljivko y je kar:

y = rcosE/sinφ

Koordinate urne oznake na vodoravni ravnini so tako:

(r sinE, y) = (rsinE, rcosE/sinφ)

Če pogledamo sliko zgoraj desno, potem velja za tan H = x/y = rsinE/y = rsinE/(rcosE/sinφ) = tanE sinφ,

- tako bo urni kot H na vodoravni ravnini kar:

H = tan^-1 (tanE sinφ) = atan(tanE sinφ)

Kaj imamo sedaj na razpolago:

Za palico višina 'h' na zemljepisni širini φ, če palico usmerimo vzdolž zemeljske osi (tj. pod kotom z vodoravno ravnino, ki je enaka zemljepisni širini φ in kaže proti severu), velja.

Znamo risati urne črte na vodoravno ravnino in kako označimo te črte.
H = atan(tanE sinφ), kjer je E=15°
mi pa iščemo enačbo poti, ki jo izriše senca gnomona na določen dan.

(x² + y² + v²)sin²δ = (x cos φ - v sin φ)²

Na poletni solsticij 21. junija je deklinacija Sonca 'δ'=23,43°. Zmanjšuje se skoraj linearno do 21. decembra, ko je δ=-23,43°. Nato začne spet skoraj linearno naraščati do 21. junija, ko je δ=23,43°. Zemlja potuje okrog skupnega težišča s Soncem po elipsi - kar pomeni, da se sončna deklinacija skozi leto ne spreminja linearno. Spreminja se cca s sinusno funkcijo - deklinacijski kot se tako lahko natančneje izračuna z enačbo
δ = arcsin[ sin( - 23.436° ) · cos ( ( N + 10 )360°/365.24 + (360°/π)0.0167 sin( ( N - 2 )360°/365.24 ) ) ]
N je število dni od polnoči UT, ko se začne 1. januar (tj. dnevi rednega datuma -1) in lahko vključuje decimalke za prilagoditev z lokalnim časom pozneje ali prej v dnevu. Število 2 v (N-2) je približno število dni po 1. januarju do perihelija Zemlje. Število 0,0167 je trenutna vrednost ekscentričnosti Zemljine orbite. Največje napake v tej enačbi so manjše od ± 0,2°.
Linearnost je le približek, ko zanemarimo napako, ki jo povzroča majhna ekscentričnost zemeljske orbite. Zato je, če privzamemo linearnost, za vse deklinacijske kote za vse dni v letu mogoče dobiti s preprosto linearno interpolacijo. A bolje je uporabiti zgornjo enačbo.
Tako lahko narišemo enačbe poti, ki jo zariše senca ob vseh datumih leta. Zato lahko ocenimo tudi datume.

4. Poglejmo, kako ta trditev deluje:

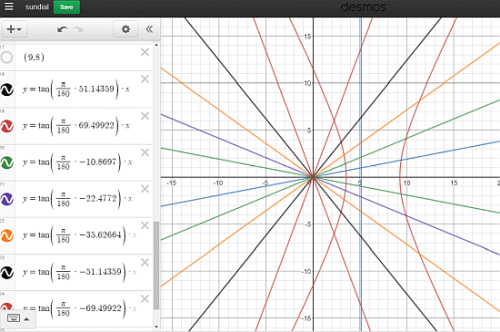
Z uporabo enačbe H = atan(tanE sinφ) poiščemo urne kote

Recimo za geografsko širino 45.777 so podatki za E° in H° naslednji:

E°   H°
15   10.869
30   22.477
45   35.626
60   51.143
75   69.499
90   90.000

Sončna ura 11

Za risanje urnih črt se lahko uporabi spletni risalnik "desmos". Upoštevajoč črto za os x kot opoldan (12 pm), potem je enačba za 11:00 uro kar y=tan (10,869).x in za 13:00 uro kar y=tan (-10,869).x in tako naprej.

Tudi za izračun poti sence po datumih in za risanje grafa se uporabi enačbo:
(x² + y² + v²)sin²δ = (x cos φ - v sin φ)²

Sončna ura 12

Sončna ura 13

Primer Sončne ure ali gnomona na zgornji sliki. Stranica višine 'h=5cm' je usmerjena proti severu pod kotom 45,7° (geografska širina Clermont-Ferrand) z vodoravno ravnino. Z drugimi besedami, ta stran gnomona je poravnana z zemeljsko osjo vrtenja (za pomanjšanje Sončne ure se recimo vse dimenzije deli s faktorjem 2, potem je višina gnomona je 2,5 cm).

Povezava Observations (Contd..The mathematics of shadows and time-keeping by sundials) vsebuje opažanja in težave z merjenjem časa s Sončnimi urami.

Astronomska osnova zahodnega koledarja in bistvena vloga merjenja senc (višine Sonca)

Glavni astronomski cikli so torej dan (na podlagi rotacije Zemlje okrog lastne osi), leto (na podlagi potovanja Zemlje okrog Sonca, letnih časov) in mesec (na podlagi potovanja Lune okoli Zemlje). Zapletenost koledarjev tiči v dejstvu, ker ti cikli ne obsegajo celega števila dni, in ker časovno niso stabilni. Oglejmo si težave s koledarjem. Siderski ali zvezdni dan (obrat Zemlje glede na oddaljene zvezde) traja slabe 4 minute manj kot srednji Sončev dan, ki je dolg 24 ur. Tako kot je dan definiran z zaporednimi kulminacijami Sonca (od poldneva do poldneva), je tudi tropsko ali Sončevo leto definirano s sezonskim gibanjem Sonca. Leto je v splošnem definirano s časom obhoda Zemlje okrog Sonca, a ker Zemlja precesira, je tropsko leto (čas med dvema zaporednima prehodoma Sonca čez pomladišče) za približno 20 minut krajše od zvezdnega leta in Sončev koledar mora upoštevati sezonsko gibanje (višino) Sonca. Tropsko ali Sončevo leto traja približno 365.242189 srednjih Sončevih dni. Če poenostavimo, lahko rečemo, da je leto dolgo 365 povprečnih Sončevih dni in približno 6 ur (dobrih 11 minut manj, natančneje 11.248 minut, to pomeni da z julijanskim koledarjem prehitevamo višino sonca za en dan že v 24*60 min/11.248 min = 128.0136548 letih). To je bil tudi argument, da so se v prvem stoletju pr. Kr. odločili, da bodo leta dolga 365 dni in vsako četrto leto (imenovano prestopno) za dan daljše, torej dolgo 366 dni. V štirih letih se namreč nabere razlika približno enega dneva (4X6 ur = 24 ur = 1 dan). Koledarsko reformo je leto 46 pr. n. št. izpeljal J. Cezar (svetoval pa mu je imeniten astronom in matematik, Grk Sosigen). Dogovorjeno je bilo, da so prestopna leta vsa tista, katerih letnica je deljiva s štiri. To je bil julijanski koledar, ki je v večjem delu Evrope veljal do 16. stoletja, v Rusiji pa celo do leta 1918. Povedali smo že, da leto ne traja točno 365 dni in 6 ur, ampak dobrih 11 minut manj, kar je naneslo do konca 16. stoletja že zamik desetih dni. V štiristo letih se namreč naberejo že dobri trije dnevi preveč (približna ocena 400X11 min ), zato so leta 1582 odvzeli 10 dni, ki so se nabrala od uvedbe julijanskega koledarja in s tem uvedli gregorijanski koledar.
Zakaj cca 10 dni razlike? Veljavno krščansko datiranje velike noči je bilo definirano na Nicejskem koncilu leta 325 in večinoma temelji na starejšem judovskem koledarju in razmerju med polno luno in enakonočjem. Prej je bila velika noč v celoti povezana z judovskim verskim praznovanjem pashe (beg Judov iz Egipta, Exodus - Izhod, glejte 2Mz 12,1-50) in še danes ima to povezavo. Nicejski koncil je prešel na julijanski sistem datiranja velike noči in takrat še ni bilo dovolj očitno, da ima julijanski koledar napako (v cca 128 letih je prehiteval za en dan), kar je pomenilo, da datum enakonočja sčasoma ni bil več usklajen z dejanskim dogodkom (z višino Sonca na prvi pomladni dan). Če pogledamo razliko let 1582 in 325 ta znaša 1257 let in če to razliko delimo s periodo 128, ki da napako enega dneva (izračunali zgoraj), dobimo zamik (prehitevanje) že za 10 dni, saj velja:
(1582 - 325)/128.0136548 = 9.82 dni ≈ 10 dni.
In še o reformi koledarja - kdaj in kako stopi v veljavo gregorijanski koledar?
Četrtku 4. oktobra 1582 je sledil prvi dan gregorijanskega koledarja, to je petek 15. oktobra 1582 (cikel prehoda med tedni ni bil prizadet). Da se napaka ne bi spet ponovila (večala), so Gregorijanski koledar dodatno korigirali tako, da se v 400 letih odvzamejo že omenjeni trije odvečni dnevi. Ti trije dnevi se odvzamejo tako, da se tri prestopna leta štejejo kot navadna. To so leta, katerih letnice se pišejo z dvema ničlama na koncu (prehodi med stoletji) in niso deljiva s 400 (to rešitev je predlagal Luigi Lilio). Zdaj tudi razumemo, zakaj sta leti 1600 in 2000 prestopni, leta 1700, 1800 in 1900 pa niso bila prestopna (so sicer deljiva s 4 a ne s 400). Resnici na ljubo tudi gregorijanska korekcija ni rešila težav s koledarjem, saj se bo napaka enega dneva spet nabrala v dobrih 3200 letih ( 400*11.248/(60*24) dni = 3.1244 dni na 400 let, napaka enega dneva se pa spet pojavi, zaradi 0.1244 dni ostanka, v približno 400*1/0.1244 let = 3215,4 letih). Papež, po katerem se koledar tudi imenuje, je reformo koledarja razglasil 24. februarja 1582 z bulo Inter gravissimas in to v vili Mondragone v Frascatiju blizu Rima, o čemer priča vgrajena plošča (reformo je pripravila posebna komisija na podlagi predloga nemškega astronoma Christophera Claviusa in neapeljskega zdravnika, astronoma in fizika Luigija Lilia). Liliov predlog je vključeval zmanjšanje števila prestopnih let v štirih stoletjih s 100 na 97, tako da bi tri od štirih let, ki se končajo z dvema ničlama (prehodi med stoletji), privzeli za običajne s 365 dnevi, namesto prestopnih let.
Omenimo še, da seveda obstaja več možnih rešitev za tropski (Sončev) koledar, recimo Hajamov koledar (napako enega dneva baje doseže v 5000 letih), trenutno najbolj natančen koledar je iranski (leta 1925 so precej zapleteno prenovili stari perzijski koledar - le na vsakih 3,8 milijona let kopiči enodnevno napako. A se je prehod iz julijanskega v natančnejši koledar najlažje zgodil preko gregorijanske reforme. Pozna samo tri dodatne izjeme na 400 let, glede na takrat utečen julijanski koledar in zamik zgolj enega dneva v 3200 letih (zelo elegantna rešitev). So debate, zakaj Evropa recimo ni prevzela Hajamovega koledarja – a gregorijanska reforma je izjemna, saj ni zahtevala prehudih posegov v julijansko prakso (v staro Sosigenovo antično reformo).

Prvi del prispevka o poti senc, ki jih tvorijo Sončevi žarki, je bil v bistvu namenjen razlagi, kako so sploh določali višino Sonca, oziroma letne čase, recimo pomladno enakonočje. In kaj so leta cca 1580 pokazali papežu Gregorju XIII. (papež od 1572 do 1585), da so ga prepričali v nujnost reforme? Problem julijanskega koledarja je bila velika napaka glede na višino Sonca, ki je v 16. stoletju že znašala 10 dni (danes je razlika že 13 dni, konec stoletja pa bo že 14) in tako se izračuni velike noči niso ujemali z astronomskimi dejstvi, letni časi pa so bili, kot smo že omenili, zamaknjeni že za kar 10 dni ...

Takrat je bilo privzeto, da se pomlad začne 21. marca. In kaj nam pove pot sence ob enakonočju? Ob enakonočju se senca giblje premo (ravna črta). In že nekaj časa so opažali, da se senca giblje premo 11. marca in ne 21. marca. In to pot sence so pokazali tudi papežu Gregorju XIII. in tako se je reforma končno odobrila. V resnici so mu pokazali pot žarkov skozi odprtino na vrhu kupole v stolpu vetrov v Vatikanu (Rim).

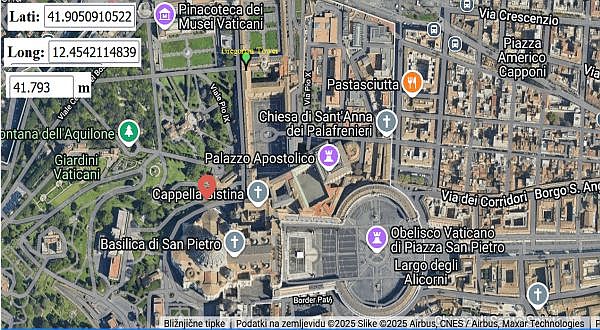
Vatikan in lega Gregorijanskega stolpa ("Gregorian Tower"), označuje ga zelen marker - Google Maps (spletno priredil Zorko Vičar).

Meridianska soba (levo) v Stolpu vetrov (desno), Vatikan ("Room of the Meridian, Tower of Winds, Vatican").
Obiskovalci Galerije zemljevidov v Vatikanskih muzejih se redko zavedajo čudeža, ki je tik nad njihovimi glavami. Na severni strani galerije se dviga večini malo znani Stolp vetrov, ki je ena najvišjih točk v Vatikanu. Med letoma 1578 in 1580 ga je postavil bolonjski arhitekt Ottaviano Mascherino. Stolp vetrov je dobil ime po anemoskopu, vetrnici, to je instrumentu, ki meri smer vetra, ki ga je zasnoval Ignazio Danti, papeški astronom. Kljub svojemu imenu pa je papež Gregor XIII. stolp posvetil le enemu namenu, to je astronomiji - za popravek napake starega Julijskega koledarja. Po pričevanjih zgodovinarjev je papež Gregor XIII. 21. marca 1581 (julijanski koledar), stopil v stolp in videl takratno veliko razliko višine, poti Sonca od pomladnega enakonočja, ki je bila takrat v dnevih že 10 dni, in se je enakonočje (pomlad) zgodila že 11. marca po takratnem koledarju. Problem velike rastoče napake koledarja so poznali že veliko prej, a resno so se ga je lotili že med Tridentinskim koncilom leta 1563, razrešili pa leta 1582. To kaže, da se je RK cerkev problema lotila znanstveno - druge ločine (protestanti, pravoslavni del sveta) so bili strogo proti reformi, raziskovanju. Sveto pismo so brali dobesedno ...

Napaka 21. marca po julijanskem koledarju v 16. stoletju - Sonce ob kulminaciji ni zadelo meridiana v točki pomladišča, ker je bil takrat koledar že zamaknjen 10 dni glede na višino Sonca.

Levo - papež Gregor XIII. (1502 - 1585), na sredi - astronom, matematik Christopher Clavius (1538 - 1612), desno - fizik, astronom, zdravnik Aloysius Lilius (c. 1510 Ciro, Calabria – 1576 Rim) - matematični oče gregorijanskega koledarja. Kot razberemo iz letnic, je umrl kar 6 let pred uvedbo njegovega novega koledarja. Študira in deluje v Neaplju. Čeprav je bil v času, ko je bil njegov predlog predstavljen v Rimu, še živ, se zdi, da ga ni on osebno predstavil - z njegovimi astronomskimi predlogi in izračuni se je ukvarjal njegov mlajši brat Antonio, prav tako zdravnik in astronom. Pravijo, da je Aloysius Liliu morda predvidel zmedo in jezo, ki bosta sledila po sprejetju koledarja, ki bo (je) ljudi "oropal" deset dni življenja! V resnici nobena koledarska reforma ni minila mirno ... No sedaj imamo še okrog 3000 let miru pred novo majhno reformo štetja dni in let - ko v našem koledarju spet nastopi razlika enega dneva (glede na višino Sonca).
Clavius ima na Luni tudi znameniti krater. Clavius in Galilej sta se dobro razumela. Rokopis Liliusa ni bil nikoli natisnjen in ni bil nikoli odkrit. Njegova vsebina je znana le iz rokopisnega poročila komisije za reformo koledarja in iz dela "Compendium of Ciaconus", ki ga je natisnil Clavius.
Kar nekaj evropskih narodov in njihovih kolonij je 1. januar uradno sprejela za novoletni dan nekoliko pred sprejetjem gregorijanske koledarja (prej se je novo leto začelo z marcem). Nekateri pa nekoliko pozneje z uvedbo gregorijanske koledarja.

Detajl iz grobnice papežev umetnika Camilla Rusconija (dokončan 1723). Antonio Lilio (Aloysius Lilius) se priklanja papežu in predstavlja svoj tiskani koledar. Ta motiv je potrebno razumeti v prenesenem pomenu - Aloysius Lilius je namreč umrl 6 let pred sprejetjem njegovega koledarskega algoritma.
https://en.wikipedia.org/wiki/Gregorian_calendar

Mnoge protestantske države so sprva nasprotovale sprejetju katoliške novosti, znanosti. Nekateri protestanti so se bali, da je bil novi koledar del zarote, ki bi jih vrnili v katoliško krilo. Na primer, Britanci zelo dolgo (do leta 1752) niso sprejeli katoliškega sistema štetja let in dni - izrecno so mu nasprotovali. Švedi so ga sprejeli leta 1753.

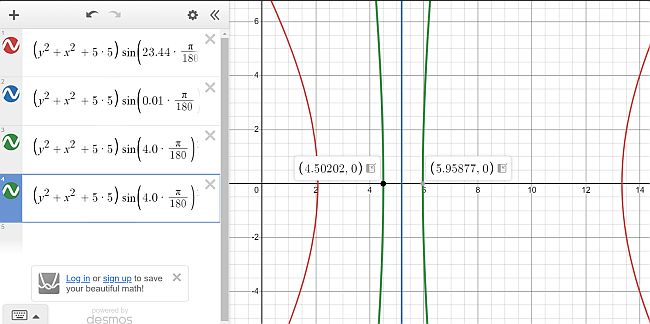
Iz slike sem ocenil višino odprtine za sonce na 5 m - Meridianska soba v Stolpu vetrov, Vatikan. Izrisal sem razliko poteka žarka za našo ge. širino, gre zgolj za oceno, za 10 dni pred in po pomladnem solsticiju. Podatke sem dobil preko kalkulatorja lege Sonca:
http://www2.arnes.si/~gljsentvid10/visina_sonca01a.html - zelo uporabno. Razlika v deklinaciji je okrog 4 ° - 0 ° = 4 °, deklinacija Sonca ob enakonočjih je seveda 0 °. Iz slike lahko razberemo, da je odmik od ravne črte sence (poti žarka) enakonočja, ki teče v smeri vzhod - zahod (modra črta) 10 dni pred ali po enakonočju, kar okrog pol metra. Os X predstavlja meridian. Torej žarek nikakor ne more zadeti pomladišča, to je presečišča modre linije in meridiana x (črna vodoravna linija) v zamiku 10 dni glede na pravo enakonočje. In tole veliko razliko so pokazali papežu Gregorju XIII. ... in bila je očitna! To se je po pričevanjih zgodovinarjev zgodilo 21. marca 1581 (julijanski koledar), ko je papež Gregor XIII. stopil v stolp in videl takratno veliko razliko višine, poti Sonca od pomladnega enakonočja, ki je bila takrat v dnevih že 10 dni, in se je enakonočje (pomlad) zgodila že 11. marca po takratnem koledarju.
Seveda sem za izračune uporabil spodnjo enačbo (izpeljali zgoraj) poti sence ali Sončevega žarka skozi odprtino:
(x² + y² + v²)sin²δ = (x cos φ - v sin φ)²

Če vas tematika zanima, lahko sami izvedete meritve in blizu enakonočij pomerite pot sence (recimo 10 dni vsak dan pred enakonočjem in po enakonočju) in s tem postanete priča napake julijanskega koledarja v 16. stoletju, ki so jo astronomi pokazali v takrat novem vatikanskem observatoriju papežu Gregorju XIII. Papež je tako pogumno sprejel reformo koledarja - ki se po njem imenuje gregorijanski koledar. Observatorij se imenuje Gregorijanski stolp ("Gregorian Tower") ali tudi stolp vetrov (na vrhu je namreč tudi vetrnica, anemoskop, ki meri smer vetra). S tako vajo boste zares dojeli težavo pri oblikovanju ustreznega algoritma za določitev ustreznega koledarja, ki mora kar se da verno sledi višini Sonca. Matematični oče gregorijanskega koledarja je fizik, astronom, zdravnik Aloysius Lilius (c. 1510 Ciro, Calabria – 1576 Rim). Umrl kar 6 let pred uvedbo njegovega novega koledarja - algoritma.

Kakšna dva meseca po zapisu tega članka, sem zasledil točnejše podatke o Gregorijanskem stolpu. Vesel sem bil, da je moja ocena o višini odprtine v steni bila dovolj točna, da ne rabim računati novih ocen o zamiku poti svetlobnega žarka glede enakonočje v zamiku desetih dni. Korekten podatek o višini odprtine je 5,2 m nad vodoravnimi tlemi (jaz sem jo iz slik ocenil na 5m), premer odprtine je cca 4 cm.

Stabilen koledar nam bistveno lajša življenje, načrtovanje.
Če je koledar usklajen z navideznim letnim gibanjem Sonca, je to velika prednost pri načrtovanju vsakdanjega življenja, pri različnih analizah dogajanja po letih, mesecih, letnih časih - recimo pri enotnih meteoroloških statistikah. Tudi vsi računalniški procesorji spletnih serverjev delujejo po taktu koledarja z enotnim greeniškim časom. Koledar je tako vgrajen v vsa relevantna računalniška orodja, programe, relacijske baze in ker je gregorijanski koledar matematično enoličen in hkrati zelo dobro sledi letni višini Sonca, je z njim enostavno upravljati. Danes noben ne pomisli, da bi kaj kompliciral s koledarjem, recimo pri izdelavi meteoroloških statistik. Zakaj, ker je Gregorijanski koledar sinhron z višino Sonca (vsaj za cca 3200 let). Če pa recimo danes primerjamo mesečne statistike (primer na spodnjem grafu) gregorijanskega in julijanskega koledarja (zamik je že 13 dni), pa vidimo, da so recimo povprečne mesečne temperature med sabo zamaknjene tudi za več kot 3 °C.
To ne bi bil tak problem, če sam julijanski koledar ne bi s cca stoletjem pridobil kar dodatni dan zamika glede višino Sonca, to je glede na gregorijanski koledar. Tako je recimo težko primerjati mesečne statistike za stoletja stare podatke v julijanskem koledarju - v gregorijanskem koledarju to ni problem. Na letnih statistikah se to sicer ne pozna bistveno - ker se zamik v povprečju dokaj dobro izniči. Velike razlike se tako pojavljajo tudi pri fenoloških fazah (recimo datumih cvetenja rastlin). V dobrih 3000 letih, ko bo gregorijanski koledar nabral napako enega dneva, bo julijanski koledar nabral že blizu 40 dni razlike. Takratne mesečne, datumske primerjave v julijanskem koledarju z današnjim časom bodo nesmiselne, v gregorijanskem pa ne bo nobenih težav. Recimo s primerjanjem mesečnih povprečnih temperatur, temperaturnih ekstremov, datumov fenoloških faz, številom ur Sončevega obsevanja, energije Sonca, kumulative padavin, višin snežne odeje. Da ne govorimo, da bo takrat pot na morje ali trganje grozdja, pobiranje krompirja, vrnitev živine iz planin ... v začetku septembra po gregorijanskem koledarju pričakovano opravilo. Po julijanskem koledarju pa nikakor ne (velja za naše geografske širine).
Časovno stabilen koledar nam torej, ne da bi se danes tega sploh zavedali, bistveno olajša življenje. In to je bil tudi glavni argument, da so tudi najbolj trmoglave dežele, države, po stoletjih iracionalnega zavračanja gregorijanskega koledarja, le tega končno sprejele.

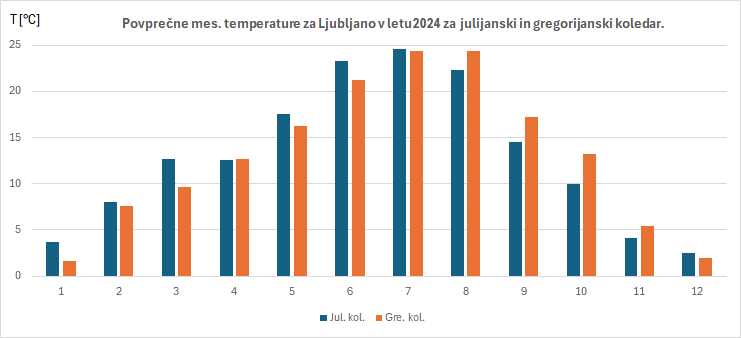
Primerjalni graf povprečnih mesečnih temperatur za Ljubljano v letu 2024 za julijanski koledar in gregorijanski, klimatološki termini. Pričakovana in očitna je razlika med povprečji jeseni in spomladi (razlike so tri ali več stopinj) - predznak razlik je nasproten. Časovno stabilen koledar nam torej, ne da bi se danes tega sploh zavedali, bistveno olajša življenje. In to je bil tudi glavni argument, da so tudi najbolj trmoglave dežele, države, po stoletjih iracionalnega (ideološkega) zavračanja gregorijanskega koledarja, le tega končno sprejele.
Časovno stabilen koledar nam torej, ne da bi se danes tega sploh zavedali, bistveno olajša življenje. In to je bil tudi glavni argument, da so tudi najbolj trmoglave dežele, države, po stoletjih iracionalnega zavračanja gregorijanskega koledarja, le tega končno sprejele.

Tabela povprečnih mes. temperatur [° C] za Ljubljano v letu 2024 za julijanski koledar in gregorijanski.

Meseci	Jul. kol.	Gre. kol.	Razlike
1	3.7			1.6	-2.1
2	8			7.6	-0.4
3	12.7			9.6	-3.1
4	12.6			12.7	0.1
5	17.6			16.2	-1.4
6	23.3			21.2	-2.1
7	24.6			24.4	-0.2
8	22.3			24.4	2.1
9	14.5			17.2	2.7
10	10			13.2	3.2
11	4.1			5.4	1.3
12	2.5			2	-0.5

V tem stoletju velja, da se prvi januar v julijanskem koledarju začne 14. januarja po gregorijanskem koledarju. Da sem dobil te primerjave, sem moral telovaditi z datumi (v PSQL-u), pri gregorijanskem koledarju pa to ni potrebno. To v svetu računalniških algoritmov sicer ni problem - je pa problem, ko se ti počasi zamaknejo letni časi, fenološke faze ... in moraš ves čas preračunavati, kaj je primerljivo s čim ... Že poletni čas je naredil ogromne škode (tudi pri meteoroloških opazovalcih ...) in ta norost se še kar nadaljuje - "Quo Vadis, Europa?".

Delno povzeto po:
https://ucatholic.com/blog/the-little-known-tower-of-the-winds-inside-the-vatican/
https://www.tiffany-parks.com/blog/2010/05/10/the-tower-of-winds-and-the-gregorian-calendar
https://amateurastroblog.wordpress.com/2016/06/26/the-mathematics-of-shadows-and-time-keeping-by-sundials/
https://www.newadvent.org/cathen/09247c.htm
http://www.naplesldm.com/lillo.php
https://en.wikipedia.org/wiki/Aloysius_Lilius
https://en.wikipedia.org/wiki/Gregorian_calendar
https://www.encyclopedia.com/science/dictionaries-thesauruses-pictures-and-press-releases/rheticus-george-joachim

Povzel Z. Vičar (2. jan. 2025)

---------------------------------------------

DODATEK - izjemen članek Miloša Rybarja iz 1983 - Gregorijanski koledar uporabljamo že 400 let.
Dodal 29. mar. 2026 - našel sem ga, ko sem s poškodovano mamo doživljal lepe trenutke, hkrati pa tudi veliko hudih preikušenj, ki jih s sabo prinese poškodba, demenca, realnost podhranjenega zdravstvstvenega sektorja. V Lj. (ko sem moral kdaj iz Koga v Lj. v pisarno) sem ji kazal Mohorjeve koledarje od Marjetke ... Tako sem slučajno zagledal ta izjemen članek - ki razkriva, kako težko je v življenje spraviti reformo (v tem primeru koledarja), kljub temu, da nam ta veliko več da, kot vzame ... Res zanimiv nauk.

https://www.dlib.si/results/?query=%27srel%3dMohorjev+koledar%27&pageSize=25&sortDir=ASC&sort=date&fyear=1983&sortDir=ASC
Mohorjev koledar 1983 (1983)
Vir: Mohorjev koledar
Izvor: Osrednja knjižnica Celje
1. PDF datoteka (30 MB)
1. TXT datoteka (768 kB)

Gregorijanski koledar uporabljamo že 400 let

Na naš koledarski sistem, ki ga stalno uporabljamo, smo se navadili in nam je tako domač, da si kar ne moremo misliti, da bi bil lahko kako drugačen. Ko bo ta članek v tisku, bo poteklo štiristo let, odkar je stopil v veljavo dekret papeža Gregorja XIII. o reformi koledarja, v letu 1983 pa bo štiristo let, kar ga uporabljamo v naših krajih.

Pri starih Rimljanih je bil do Cezarjeve reforme v veljavi koledar, ki je bil urejen po luninem letu, to je po luninih menah. Tako leto je seveda krajše, zato so imeli rimski svečeniki pravico, da so, ko je bilo potrebno, vstavljali v koledar poseben »vmesni« oz. prestopni mesec (mensis intercalaris), da so dosegli dolžino sončnega leta. S takšnim vstavljanjem mesecev ali samo nekaj prestopnih dni so lahko tudi umetno podaljševali čas vladanja rimskih funkcionarjev (konzulov itd.), ki so bili sicer izvoljeni samo za eno leto. V času rimskega diktatorja Julija Cezarja je bite že prava koledarska zmešnjava in se koledar ni več ujemal s pravimi letnimi časi. Julij Cezar si je nabral že vse funkcije, ki jih je poznala takratna rimska republika, in ko je postal še vrhovni svečenik (pontifex maximus), je dobil pravico reformirati koledar. Po nasvetih aleksandrijskega astronoma Sosigena in rimskega astronoma Flavija je leta 46 pred Kristusom odredil koledarsko reformo, s katero je z naslednjim letom vpeljal egipčansko sončno leto, s katerim se je seznanil, ko je malo pred tem bival v Egiptu. Koledarska zmešnjava je bila tedaj že tolikšna, da je bilo treba pred uvedbo reforme poleg običajnega prestopnega meseca v februarju s 23 dnevi, vriniti med november in december še 67 »vmesnih« oziroma prestopnih dni, da so dosegli sončno leto. Tisto leto je bilo dolgo kar 445 dni in so ga imenovali »annus confusionis« (leto zmešnjav) ali »annus confusionis ultimus« (zadnje leto zmešnjav, ker bo z reformo namreč drugače). Po egipčanskih izračunih je bila dolžina (sončnega) leta 365 dni in 6 ur, zato je Cezar odredil, naj si sledijo tri leta po 365 dni, četrto leto pa naj bo prestopno s 366 dnevi (s prestopnim dnem v februarju). Za začetek leta je Cezar določil 1. januar (do tedaj je bil pri Rimljanih začetek 1. marec). Uredil je tudi dolžino 12 mesecev. Ta koledar s sončnim letom in s prestopnim vsakim .. četrtim letorh se p>o Cezarju imenuje julijanski koledar in je ostal v Evropi v veljavi ves srednji vek. Krščanstvo je namreč ta način prevzelo, ostalo je tudi dvanajst mesecev s svojimi latinskimi imeni. Na novo so uvedli le teden in krščanske praznike z veliko nočjo vred (na prvo nedeljo po pomladni polni luni).

Leta 1200 so prvič opazili neskladje med julijanskim koledarjem in sončnim letom. Koledar je namreč že nekaj dni zaostajal za letnimi časi. Angleški naravoslovec in filozof Roger Bacon (1214-1294) je papežu Klementu IV. prvi predlagal reformo julijanskega koledarja. Astronomi, ki so se leta 1252 zbrali po ukazu kastiljskega kralja Alfonza X., so že izračunali, da je dolžina leta 365 dni, 5 ur, 48 minut in nekaj sekund, torej julijanski koledar zaostaja za 11 minut in nekaj sekund letno. Ta zaostanek je v XV. stoletju znašal že 9 dni, k^r vidimo tudi iz vremenskih pregovorov, ki so v tistem času nastali. Tako velja npr. po kmečkem koledarju god sv. Gregorja Vel. (12. marca) za prvi pomladanski dan in v

Papež Gregor XIII. s komisijo za reformo koledarja

Vir: https://www.bridgemanimages.com/en/noartistknown/pope-gregory-xiii-chairing-the-commission-for-reforming-roman-calendar-1582-1583-illustration/nomedium/asset/593197

nekaterih krajih ta darfspuščajo p» vodi razsvetljene hišice ali cerkvice v znak, da je odslej možno v popoldanskem času delati brez razsvetljave. Danes se nam tak datum za začetek pomladi zdi smešen in tudi pri luči moramo še delati. Toda če prištejemo temu datumu 9 dni, dobimo 21. marec, to pa je že pomlad in pomladno enakonočje. Trubarjeva pesem: »Šent Vid (15. junij) ima dan nerdalši, Lucija (13. december) pak ner ta kratši... Sveti Gregor (12. marec), mali križi (14. september) dasta nuč, dan v eni viži,« razumemo lahko le tako, da dodamo vsem datumom še 9 ali 10 dni, kolikor je pač znašala razlika v koledarju (za poletni sončni obrat moramo pri tem vzeti datum p» kmečkem koledarju, ki ga postavlja na 24. junij).

Tako velika razlika v zaostanku koledarja je bila vzrok, da sta se v XV. stoletju že vesoljna cerkvena zbora v Constanzi in Baslu na predlog kardinalov Pierra d'Aillyja in Nikolaja Cusanusa ukvarjala z vprašanjem reforme koledarja. Papež Sikst IV. je dosegel, da je prišel v Rim učenjak
4 Koledar 1983
49
Johann Miiller, imenovan Regiomontanus, ki naj bi pripravil koledarsko reformo, toda leta 1476 je umrl. Razlika je v tem času narasla ae na 10 dni, tako, da je na prvi pomladanski dan kazal koledar šele 11. marec. Predlogi za reformo so se množili, s tem se je ukvarjal tudi V. lateranski vesoljni cerkveni zbor. Končno pa je tridentinski vesoljni cerkveni zbor na svoji seji 4. decembra 1563 poleg reforme rimskega misala in brevirja naročil papežu, naj reformira tudi koledar. Liturgične knjige je takoj reformiral papež Pij V., koledarske reforme pa se je lotil papež Gregor XIII. (Ugo Buonconpagni, roj. 1502, papež od leta 1572 do smrti leta 1585). Za osnovo reforme je bilo delo, ki ga je pripravil napolitanski zdravnik in matematik Luigi Giglio Ghiraldi (Aloisius Lilius) in ga je po njegovi smrti (1576) predložil brat Antonio. Papež je imenoval posebno komisijo, v kateri so bili strokovnjaki raznih narodnosti in ki je pod vodstvom kardinala Sirleta izdelala dokončni predlog. Glavno delo v komisiji je opravil nemški matematik Christoph Clau (Clavius) iz Bamberga. Papež je predlog poslal tudi katoliškim vladarjem in katoliškim univerzam. Končno je 24. februarja 1582 papež podpisal bulo »Inter gravissimas« o reformi koledarja, ki se po papežu imenuje gregorijanski koledar.

Glavna točka gregorijanske reforme je. bila da preskoči 10 dni in s tem odpravi koledarski zaostanek, kakor pač potisnemo naprej kazalce pri uri, ki zaostaja. Papež je določil, naj po 4. oktobru tistega leta sledi takoj 15. oktober. Tako je začetek pomladi padel spet na 21. marec, kakor je to določil že vesoljni cerkveni zbor v Niceji leta 325. Da bi se pa v bodoče spet ne nabirala razlika zaradi tistih letnih 11 minut in nekaj sekund, je papež odredil, da so pri okroglih stoletjih samo tista prestopna, ki so deljiva s 400; torej je bilo leto 1600 prestopno, leta 1700,1800 in 1900 pa ne, četudi bi po julijanskem koledarju morala biti prestopna, leto 2000 pa bo spet prestopno. Ta sistem je tako dobro preračunan, da se bo šele čez 3333 let nabrala razlika za 1 dan. Te določbe papeževe bule je bilo treba sedaj saino uresničiti, toda pri tem so se že pojavile težave. Kakor je od prvega predloga za reformo pa do bule »Inter gravissimas« poteklo 400 let, tako je spet poteklo skoraj 400 nadaljnjih let, da je bil julijanski koledar zamenjan z gregorijanskim, saj so nekatere evropske države šele v tem stoletju uvedle gregorijanski koledar.

Težava pri uveljavljanju gregorijanskega koledarja je bila ta, da je bil papež verski poglavar in ne državni. Kjer je bil papež tudi državni poglavar, to je v Cerkveni državi, tam je šlo seveda brez težav. Najbolj katoliški državi, Španija in Portugalska, sta koledar uvedli z oktobrom, Francija pa z decembrom 1582. V nemških deželah (cesar je bil tedaj Rudolf II. Habsburški) so o • tem razpravljali na državnem zboru v Augsburgu in sklenili, naj uvedejo gregorijanski koledar katoliški knezi, protestantski in kalvinski knezi pa naj ostanejo pri starem (julijanskem) koledarju. Cesar je 4. septembra 1583 (po starem) odredil uvedbo gregorijanskega koledarja in v odloku iz previdnosti sploh ni omenil papeža. V Nemčiji so bile tedaj polemike med katoličani in reformiranimi kristjani na višku, vendar je nekoč Luter posebej poudaril, da koledarska reforma ni verska zadeva, zato naj ne bi razvnemala strasti. Posamezni glasovi med protestanti (evangeličani), tako npr. teolog Martin Chemnitz in meščan Barrtholomäus Scultetus iz mesta Görlitz sta se izrekla za gregorijanski koledar. Toda prevzem tega koledarja je bil povod, da so protestanti začeli divje napadati gregorijanski koledar, papeža in katoličane. Lukas Osiander, wiirtemberški dvorni pridigar, je zatrjeval, da je namen gregorijanskega koledarja porušiti verski mir. Iz papeževega grba, v katerem je bil zmaj, je prerokoval krvavi pokol v Nemčiji, ki naj bi ga po njegovem mnenju pripravljal papež. Tiibinški profesor teologije Jakob Heerbrand je trdil, da je gregorijanski koledar delo Satana, in da zato ni treba ubogati oblasti, ki ukazuje tak koledar.

Naše dežele (Kranjska, Štajerska in Koroška) so tvorile tedaj posebno enoto, imenovano Notranja Avstrija z glavnim mestom Gradcem, kjer je vladal nadvojvoda Karl II. Habsburški. Ta nadvojvoda, četudi je bil prepričan katoličan, je moral zaradi turške nevarnosti protestantskemu plemstvu in meščanstvu dovoliti razne svoboščine glede njihove vere. Sedaj je nadvojvoda Kari s sklicevanjem na cesarja 25. septembra 1583 podpisal odlok, s katerim v svojih deželah uvaja gregorijanski koledar z oktobrom (torej eno leto po papeževi buli). Za tiste, ki bi tega koledarja ne sprejeli, določa kazni. Nadvojvoda je svojemu patentu priložil vzorec novega koledarja za oktober, november in december 1583. Za koledarsko reformo so se ogreli le katoličani, protestanti pa so ostali pri starem. Najbolj se je koledarska reforma poznala v poslovnem življenju, ker je 10-dnevni preskok povzročil, da sta bili v vsakem tednu dve nedelji, ena po julijanskem, druga p» gregorijanskem koledarju. Protestantski trgovci in obrtniki so praznovali eno, katoliški pa drugo. Ko so na listinah in pismih pisali datum, so odslej morali pripisati, ali je to »po novem« aH »po starem«. Nadvojvoda je 22. oktobra (po novem) pravno uredil finančne probleme, ko so nastali zaradi izpadlih 10 dni.

Za Kranjsko nimamo veliko podatkov o prehodu na novi koledar. Gospostvo (Škofja) Loka je na gregorijanski koledar preskočilo od 22. oktobra na 1. november, deželni stanovi pa 3. novembra še datirajo po starem, 18. novembra pa že po novem. Več podatkov imamo za Štajersko. Tam je nastal pravi koledarski spor. Notranjeavstrijska vlada je poslala graškemu mestnemu županu dekret, v katerem ga opozarja na različno odpiranje lokalov; kdor bo odslej še kršil nadvojvodov odlok o uvedbi gregorijanskega koledarja, naj se mu zapleni roba, ki jo ima v lokalu. Štajerski deželni stanovi (večino so imeli protestanti) so se sestali 5. (15.) novembra in protestirali pri nadvojvodu zaradi uvedbe novega koledarja. Vlada je odredila, da bo vsak dokument, ki bo od 1. januarja 1584 (po novem) datiran po julijanskem koledarju, ničen in neveljaven, ne bo dajal nikakršnih pravic in nobeno sodišče ne bo smelo takega dokumenta sprejeti; kdor odpira in zapira lokale po starem koledarju, bo kaznovan. Pri tem je vlada ponovila odredbo o zaplembi robe za kršilce nadvojvodovega odloka. Ta vladni patent je bil izobešen v Gradcu na različnih krajih, so ga pa na več mestih raztrgali in onesnažili. Zoper tako ravnanje je nastopil nadvojvoda z osebnim razglasom, v katerem je obljubil zelo visoko nagrado 500 goldinarjev tistemu, ki bi naznanil ali pomagal izslediti storilca; kazen v enaki višini doleti tistega, ki ve za storilca, pa ga ne naznani.

Zmešnjava je trajala dalje: vlada in z njo katoličani so računali, praznovali in delali po novem koledarju, plemstvo in meščani pa po starem. Da bi pomirili svojo vest, so se štajerski deželni stanovi v novembru obrnili na evangeličansko cerkveno vodstvo v Gradcu z vprašanjem, ali smejo sprejeti ta koledar. Graški pastorji so že pred tem pridigali zoper »papistični« koledar in so se v odgovoru postavili na stališče, da gregorijanski koledar izvira od papeža, zato je nesprejemljiv. To svojo odločitev so utemeljevali celo s svetopisemskimi navajanji. Koledar na novo ureja mesece in praznike, to pa je proti nauku apostola Pavla (prim. Ef 5) in proti svobodi. Papež je Antikrist, na njega se nanašajo besede preroka Danijela o zveri, ki bo požrla, pomendrala in

4*

ROMANI
CALENDARII
A-GREGORIO XIII.
P. M. R.ESTITVTI
Explicado
SDNCLEMENTIS VIII.
P.M. I V S SV EDITA.
Auflore
CHRISTOPHORO CLAVIO
BAMBER.GENSI SOCIliTATIS IESV. Acccbitconfutatio coriim,qui Calcndariuni alitcr !níbiurandum díc contcndcrunc. ROMAE, Apud AloyfiumZanncttum/ MDCIII. ' ~ /EX SVPER.IQR.VM PER.MISSV.
C V H P K 1 V I L E C 1 O.

Naslovna stran knjige iz leta 1603, v kateri jezuit Christoph Clavius razlaga koledarsko reformo (hrani NUK Ljubljana)

razdrobila vso zemljo ter bo hotela »spremeniti čase in postavo« (Dan 7, 25). Pravi kristjani ne bodo sprejemali Antikristovega napačnega in strupenega koledarja. Četudi sta cesar in nadvojvoda sprejela novi koledar, je to Satanovo delo in je treba ravnati tako kakor Makabejci, ki so raje umrli, kakor pa da bi jedli svinjsko meso. Celo na kmečki koledar in 'pregovore so se sklicevali, češ da je z novim koledarjem vse porušeno. Pastorji so menili, da stanovi lahko toliko popustijo, da pri listinah napišejo stari in novi datum, vlada pa ne sme nikogar ovirati, da bi delal in praznoval po starem. Deželni stanovi so torej sprejeli to mnenje in tako čakali na sklic stanovskega zasedanja. Zdaj pa je nadvojvoda izdal dekret, v katerem se pritožuje nad nepokorščino, ki jo kažejo deželni stanovi pri pisanju datumov; na prihodnjem zasedanju deželnih stanov želi popolno enakost pri datiranju in bo vsak, ki se bo zoper to pregrešil v besedi ali pismu, kaznovan s 1000 dukati. Deželni zbor se je sešel 8. (18.) decembra 1583. Seveda je bilo na dnevnem redu koledarsko vprašanje. Stanovi so očitali nadvojvodu, da jih s tem omejuje v njihovih svoboščinah, da uvaja koledar pod vplivom papeškega
51
nuncija in jezuitov, nadvojvoda pa jim je očital vso polemiko in neprimerne izraze, trganje plakatov itd. To razpravljanje med nadvojvodom in stanovi je potekalo pismeno, kar je trajalo do konca decembra. V prvih dneh januarja 1584 (po novem) se je razpravljanje končalo: stanovi so izjavili, da sprejemajo novi koledar zaradi pokorščine in ne iz strahu pred kaznijo.

Toda že 4. januarja 1584 je nadvojvoda za vse svoje dežele ponovil svoj patent, ker se tudi katoličani niso držali novega koledarja. 27. junija 1584 ga je ponovil že drugič. Gospostvo Poljane ob Kolpi na Kočevskem se še tedaj ni držalo novega koledarja. 5. julija je kranjski vicedom pisal lastniku tega gospostva in zagrozil s telesnimi in denarnimi kaznimi tistim, ki bi še uporabljal stari koledar. Desetdnevni preskok se je nekaterim zdel tako hud, da so se krčevito upirali reformi, vendar so katoliške dežele v nekaj letih le prevzele gregorijanski koledar, medtem ko so bile protestantske dežele »raje v nasprotju s soncem kakor pa da bi pritrdile rimskemu sedežu«. Temeljito obrazložitev koledarske reforme in zavrnitev vseh ugovorov je pripravil vodilni član papeške komisije Christoph Clavius, ki je leta 1603 izdal o tem knjigo na 682 straneh. Važno je bilo, da sta se dva vodilna svetovna astronoma, oba protestanta, izrekla za gregorijanski koledar; to sta bila Danec Tycho Brahe in Nemec Johannes Kepler. Kepler je npr. leta 1603 zapisal, da gregorijanski koledar sicer ni brez napak, je pa mnogo bolj točen kakor julijanski. Po njegovem mnenju je sramota za Nemce, ki so pripravili predloge za zboljšanje koledarja, da se še vedno upirajo koledarski reformi.

Leta 1700 bi razlika med gregorijanskim in julijanskim koledarjem znesla že 11 dni in tedaj so reformo sprejele protestantske in kalvinske dežele v nemškem cesarstvu, v Švici, na Nizozemskem ter Danska. Ko sta novi koledar sprejeli Anglija (1752) in Švedska (1753) je bilo treba preskočiti že 11 dni.

Pravoslavna Cerkev pa je trdovratno vztrajala pri julijanskem koledarju. Leta 1593 se je v Carigradu zbrala sinoda, ki je preklela gregorijanski koledar, češ da je v nasprotju z določbami nicejskega koncila. V tej obsodbi so se združili carigrajski patriarh ter patriarha iz Aleksandrije in Armenije. Leta in stoletja so minevala, za letom 1700 je prišlo leto 1800 in za njim leto 1900. Ta po gregorijanskem koledarju niso bila prestopna, tako da je sedaj razlika narasla že na trinajst dni. Rusija je do oktobrske revolucije računala čas po julijanskem koledarju, kar vidimo ravno pri imenih obeh ruskih revolucij: februarska revolucija je bila 10. marca, pri njih pa je bil po julijanskem koledarju še 25. februar; oktobrska revolucija pa je bila 7. novembra, ko so pri njih še pisali 25. oktober 1917. Prva od pravoslavnih držav je prešla na gregorijanski koledar Bolgarija leta 1917, nato leta 1918 Rusija, leta 1923 pa Grčija. Na ozemlju naše države je bil ob nastanku kraljevine Srbov, Hrvatov in Slovencev v veljavi julijanski koledar na področju Srbije, Makedonije in Črne gore. Leta 1919 so tudi tam uvedli gregorijanski koledar (prešli so z 18. na 31. januar); vendar samo za državno področje. Srbska pravoslavna Cerkev je za svoje notranje področje obdržala julijanski koledar in praznuje sve svoje nepremakljive praznike 13 dni pozneje, premakljive pa tako, kakor je tisto leto velika noč (lahko istočasno, lahko 1 teden, lahko pa tudi mesec dni razlike). Bitka na Kosovem polju je bila 15. julija 1389, toda Srbi praznujejo Vidovdan sedaj 28. junija.

Tudi pravoslavne Cerkve so končno uvidele, da nima smisla vztrajati na julijanskem koledarju. V Carigradu je bil leta 1923 vsepravoslavni kongres, ki je sprejel predlog srbskega akademika Milutina Milankoviča, da bi preskočili 13 dni. Glede prestopnih let ob zaključku stoletij pa je bil Milankovičev koledar še bolj točen kot gregorijanski, vendar zaradi cerkveno-političnih razlogov tega sklepa niso izvedli. Posamezne pravoslavne Cerkve (carigrajska, grška, ciprska, romunska) so potem tudi za notranje območje sprejele gregorijanski koledar, le računanje velike noči je ostalo drugačno. Kako so ljudje navezani na stari koledar, se je videlo v Grčiji, ko dve škofiji nista hoteli preskočiti 13 dni.

V našem stoletju je bilo že več predlogov tako pri Društvu narodov kakor pri sedanji Organizaciji združenih narodov, za korenito spremembo koledarja v njegovi notranji ureditvi. Dolžino leta, ki jo je pred 400 leti točno določil papež Gregor XIII., pa so pustili nedotaknjeno. Po julijanskem koledarju pade sedaj začetek pomladi že na 8. marec in tega koledarja se danes držijo samo še nekatere pravoslavne Cerkve za svoje interno področje (med njimi srbska in ruska). Gregorijanski koledar je šele danes doživel splošno uporabnost in lahko damo priznanje vsem tistim, ki so že pred 400 leti imeli pogum, da so to reformo kljub številnim ugovorom sprejeli.

Miloš Rybar