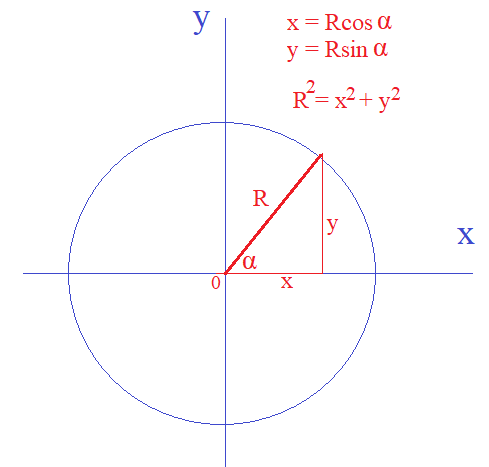Pot sence palice zaradi navideznega gibanja Sonca po nebu - alternativna izpeljava z rotacijo ravnine
iz ekvatorialne v tangentno ravnino
Klasična izpeljava je na:
pot_sence_sonca_zv_vert_pal.html.
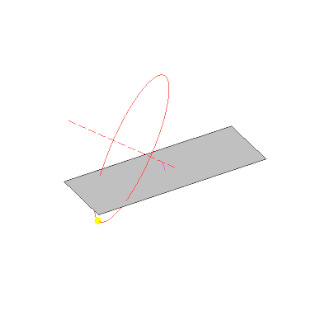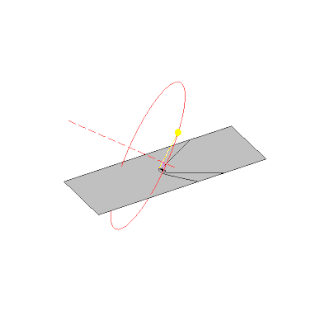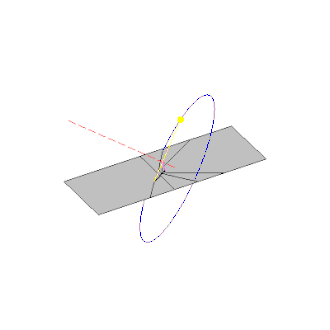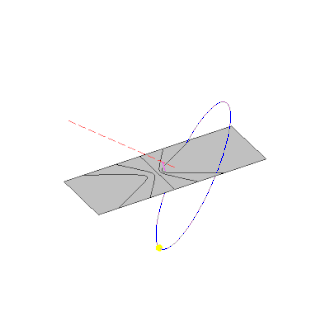
Pot sence palice zaradi navideznega gibanja Sonca po nebu.
Katere informacije lahko dobimo glede na pot sence, ki jo tvori palica?
Opazimo, da se senca (po vsaki označitvi vrha sence) premakne za neenakomerne kote in dolžine glede na časovne
intervale.
Pot sence konice pokončne palice (ali konice poljubnega ozkega telesa
z višino 'v' nad vodoravno površino) je kar enaka stožčastemu preseku (hiperboli). Zakaj?
Ker je pot sence palice stožec, bo presek tega stožca z ravnino horizonta,
ki oklepa kot φ (geografska širina kraja
opazovanja)
z osjo stožca
kar stožnica - izkaže se, da hiperbola (razen na polih, kjer je krog ali
elipsa nad ge. širino 90 ° - δ). Glejte slike in izpeljave, ki sledijo. A najprej zelo kratek povzetek,
ki bo morebiti nekaterim zadoščal:)
STRNJEN POVZETEK POTI SENCE - izhajajmo iz zgornjega uvoda in slik, ki sledijo
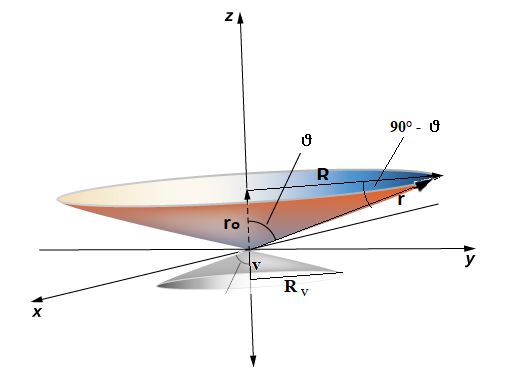
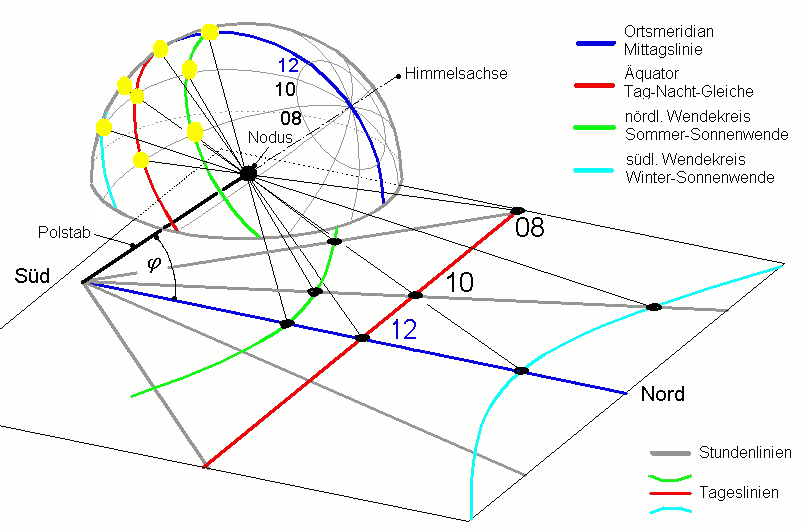
Naj bo kot δ = 90° - θ, glejte sliko levo zgoraj v koordinatnem sistemu (X, Y, Z),
to je kot med presekom (osnovno ploskvijo, ki je
krog) in plaščem stožca.
Če pogledamo stožec, velja
tan δ = Z/R, oziroma R = Z tan δ ,
enačbo še kvadriramo. Ker za krog velja enačba R2 = X2 + Y2, velja naslednji
splošen zapis:
(X2 + Y2)tanδ 2 = (Z)2
Sliki nista v merilu, razdalja do Sonca je veliko večja od polmera Zemlje, tako da ravnino ekvatorja
lahko, v mejah Zemlje, poljubno vzporedno premikamo in se s tem, za našo natančnost, geometrija sence palice ne bo
zaznavno spreminjala - bo še zmeraj enak stožec.
Ekvator tvori tisto ravnino, vzporedno s katero navidezno dnevno potuje Sonce,
to je kar dober približek (in senca pokončne palice na ravnino ekvatorja tvori stožec med dnevnim potovanjem
Sonca).
Poiščimo pa enačbo projekcije preseka stožca na ne pravokotno ravnino (glede na os stožca).
V tem primeru je ta ravnina rotacija iz ravnine ekvatorja v tangentno ravnino Zemlje
(naše opazovališče, ravnina horizonta).
Ravnina ekvatorja in ravnina našega horizonta sta zarotirani za 90 ° - φ. Na ravnini našega horizonta
tako dobimo stožnico (elipso, hiperbolo, ...). Kot φ
je geografska širina opazovališča (za naše kraje je okrog 46 stopinj).
Uporabimo torej znani transformaciji (iz srednje šole) med rotiranima koordinatnima sistemoma in ju
zamenjajmo v zgornji enačbi. Ti transformaciji se glasita (nekoliko nižje je transformacija tudi pojasnjena):
X = x'cos (90 - φ) - z' sin (90 - φ) = x'sin φ - z' cos φ
Z = x'sin (90 - φ) + z' cos (90 - φ) = x'cos φ + z' sin φ
Y = y'
Tako dobimo naslednji izraz:
((x'sin φ - z' cos φ)2 + y'2)tanδ2 = (x'cos φ + z' sin φ)2
Končni izraz za vertikalno palico dolžine z' = -v je torej kar (odpravimo še črtice x',y',z' => x, y, z):
((xsin φ + v cos φ)2 + y2)tanδ2 = (xcos φ - v sin φ)2
Zgornji zapis je torej enačba poti, stožnice (za naše kraje hiperbole), ki ji sledi
senca palice višine 'v', sedaj usmerjena navpično na Zemljino ravnino, torej na ravnino horizonta.
Iz sence palice lahko določimo letne čase, ocenimo dolžino leta, torej tudi datume,
uro v dnevu, ko sije Sonce ...
Priporočam tudi 3D spletni risalnik
'desmos 3D' - https://www.desmos.com/3d
[osnova za risanje stožca je recimo
y^2+(z-5)^2=f(x)^2
ali
y^2+x^2=f(z-5)^2, klikneš še na opcijo add slider [f]
ali
z=ax^2+by^2 - dovoliš add slider a b all (a in b parametra se spodaj na drsnikih privzeto nastavita na 1, lahko pa ju seveda spreminjaš)
ali
segment((3,0,0),(0,0,4)) - premica od do
ali
(0,0,5) - točka na osi z = 5
]
Pomoč za risanje 3d grafov z orodjem desmos:
*
https://docs.google.com/document/d/1jDJC0Zw7cB82SNEc04m5HGQHaXYaJK62iZM88ojNYwI/preview?tab=t.0
*
https://help.desmos.com/hc/en-us/articles/19796006153997-Getting-Started-Desmos-3D
*
https://blog.desmos.com/articles/beta-3d-release/
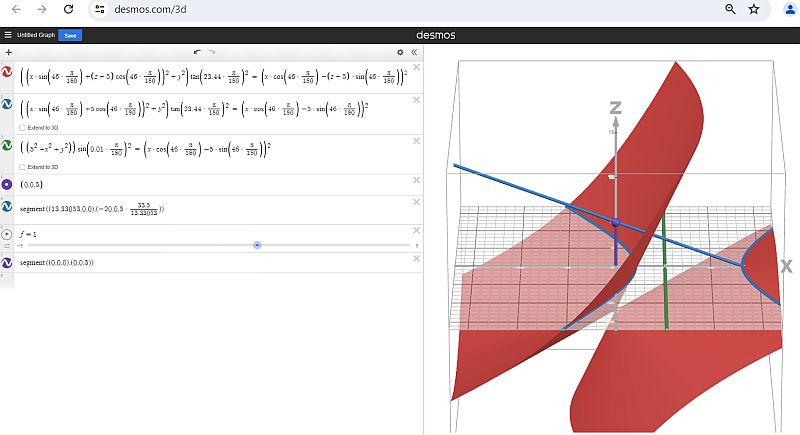
3D graf sence pokončne palice dolžine v = 5 cm. Tisto kar se lepo opazi je, da se enačba stožnice
(v tem primeru hiperbole - modri krivulji), pričakovano lepo ujema s presekom stožca na ravnini (x, y).
Enakonočji predstavlja zelena črta. Modra premica predstavlja Sončev žarek na vrhu palice ob zimskem solsticiju.
Za pote sence vstavite v 3d graf recimo enačbe:
* alternativna enačba stožca - izris:
\left(\ \left(x\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\ +\left(z+5\right)\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\right)\tan\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -\left(z+5\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
presek ravnine - alternativna enačba stožnice:
\left(\ \left(x\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\ +5\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\right)\tan\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
* presek ravnine - klasična enačba stožnice (enakonočje δ ≈ 0):
\left(\ \left(5^{2}\ +x^{2}\ +\ y^{2}\right)\right)\sin\left(0.01\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
* klasična enačba stožca - izris:
\left(\ \left(\ z+5\right)^{2}\ +x^{2}\ +\ y^{2}\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -\left(z+5\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
* presek ravnine - klasična enačba stožnice:
\left(\ \left(5^{2}\ +x^{2}\ +\ y^{2}\right)\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
* risanje pomožnih črt:
\left(0,0,5\right)
\operatorname{segment}((13.33053,0,0),(-20,0,5\cdot\frac{33.5}{13.33053}))
\operatorname{segment}((0,0,0),(0,0,5))
3D spletni risalnik
'desmos 3D' - https://www.desmos.com/3d
.
Sedaj pa se posvetimo dodatni matematično-astronomski razlagi, z več skicami,
ki je zelo poučna - je nekoliko dolga, a ne bo vam žal.
No - pa začnimo.
Sledi daljša matematična obravnava problema
Preprost primer palice na severnem polu.
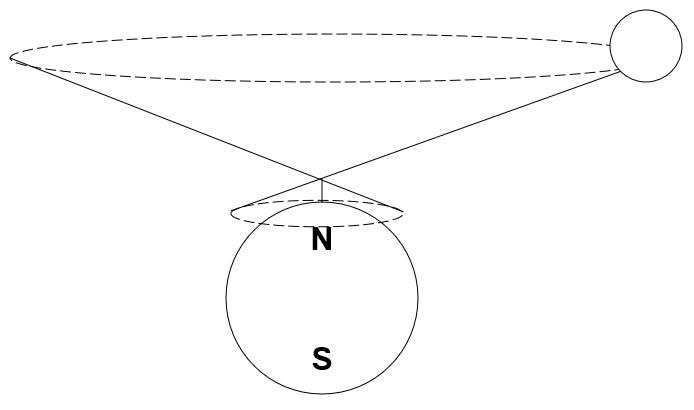
Sončna ura 1
Razmislimo o palici na severnem polu.
Ko se Sonce giblje po nebesni sferi, v enem
dnevu žarki, ki zadenejo konico palice
oblikujejo stožec (kot je prikazano na zgornjem diagramu). Sečišče
tega stožca z ravnino obzorja (palica kaže proti severu) je pot sence palice (
presečišče ravnine s stožcem je stožnica
- krog, elipsa, parabola ali hiperbola).
Oboroženi s temi spoznanji - ko
sončni žarki čez dan tvorijo
stožec z vrhom na konici palice (palica je poravnana z osjo zemeljske
rotacije) in presečišče tega stožca z ravnino
obzorja je kar iskana pot, ki jo začrta senca palice - potem lahko
problem načeloma geometrijsko zelo enostavno rešimo.
**Nebesna sfera je namišljena sfera,
ki se razteza od središča Zemlje, na kateri se zdi, da Sonce in zvezde krožijo okoli Zemlje - okoli osi rotacije
Zemlje (premikanje teles na nebesni sferi je torej večinoma posledica rotacije Zemlje).
Za nas kot opazovalce, ki se vrtimo skupaj z Zemljo,
se zdi, da se Sonce (in zvezde) vrtijo okoli zemeljske osi v nasprotni smeri rotacije
Zemlje.
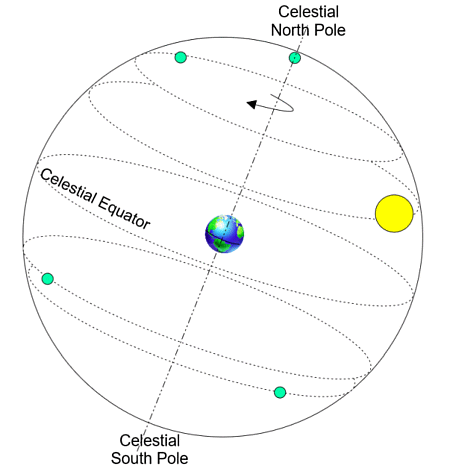
NEBESNA SFERA
2. Zdaj pa razmislimo o bolj splošnem primeru.
Preučimo palico višine 'h', usmerjeno vzdolž (vzporedno)
Zemljine rotacijske osi (na severni polobli bo taka palica, ki kaže
proti severu, ležala kar v osi rotacije) na zemljepisni širini 'φ' (podrobnosti o zemljepisni širini najdemo na:
leto in Zemljina orbita ter s tem povezana gibanja na nebu).
Sončna ura 2
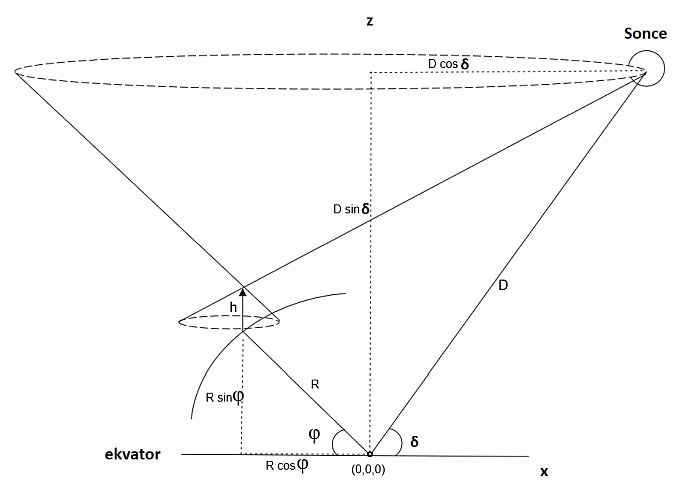
D je razdalja od središča Zemlje do Sonca in "δ" je
deklinacija Sonca.
Deklinacija Sonca je analogna zemljepisni širini. Določa
položaj Sonca na nebesni sferi. Natančneje določa, kako
daleč na severu ali jugu se nahaja ravnina gibanja Sonca
glede na nebesni ekvator. Tako kot zemljepisna širina pove, kako daleč severno, oz.
južno, leži nek kraj od zemeljskega ekvatorja (gre za kotno razdaljo).
Za razumevanje deklinacije Sonca, si oglejte spodnjo sliko, ki prikazuje začrtano pot
Sonca na nebesni sferi skozi vse leto. To pot pa imenujemo
'EKLIPTIKA' (je v resnici ravnina orbite Zemlje okoli
Sonca - skupnega težišča). Ker je os vrtenja Zemlje nagnjena
za 23,44 stopinje glede na orbito Zemlje okoli Sonca (podatki so različni), zato
Sonce v različnih letnih časih leži na različnih položajih
nebesne krogle.
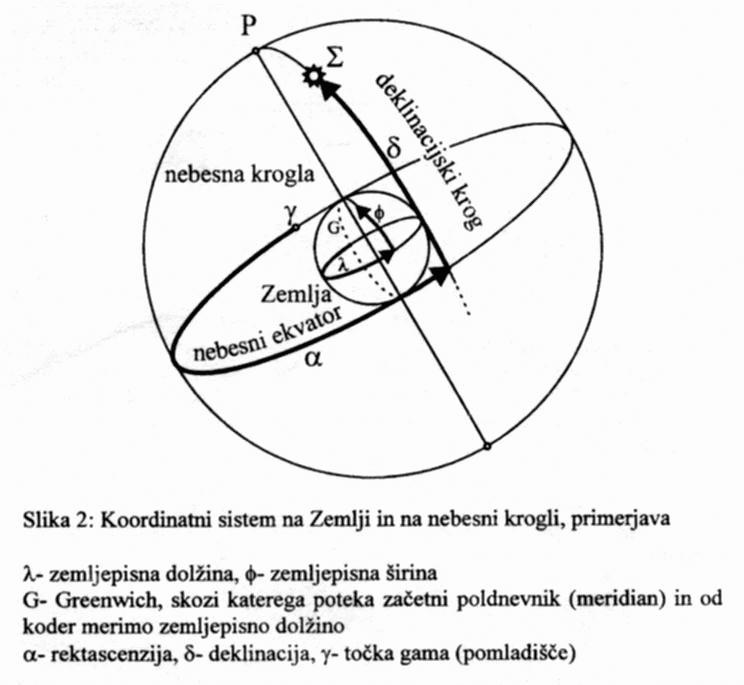
Sončna ura 3
Primerjava koordinatnega sistema na Zemlji in na nebesni krogli.
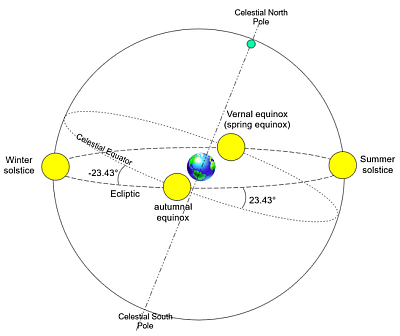
Poudarimo še: na poletni solsticij je os
Zemlje najbolj nagnjena proti Soncu: deklinacija Sonca je takrat 23,43°.
Simetrično je ob zimskem solsticiju, ko je zemeljska os nagnjena
stran od Sonca in je deklinacija Sonca: -23,43 °.
Ob enakonočju zemeljska os ni nagnjena ne stran ne proti
Sonce, deklinacija Sonca je takrat: 0 °. Zato deklinacija
Sonca skozi vse leto niha od 23,43° do -23,43°.
Če se vrnemo k
problemu, se jasno vidi, da se Sonce navidezno premika
po krogu s polmerom D cosδ in središče tega kroga
leži na višini D sinδ od središča Zemlje.
Iz prejšnje slike je razvidno, da je
središče kroga Sončnega gibanja zamaknjeno za Rcosφ od
konico palice. Ker je polmer tega kroga Dcosδ >>>
Rcosφ (D = razdalja Sonca od Zemlje, 149,6 milijona km in R = polmer
Zemlja, 6371 km), lahko štejemo, da središče gibanja Sonca
poteka vzdolž konice palice, kot je prikazano na sliki
spodaj:
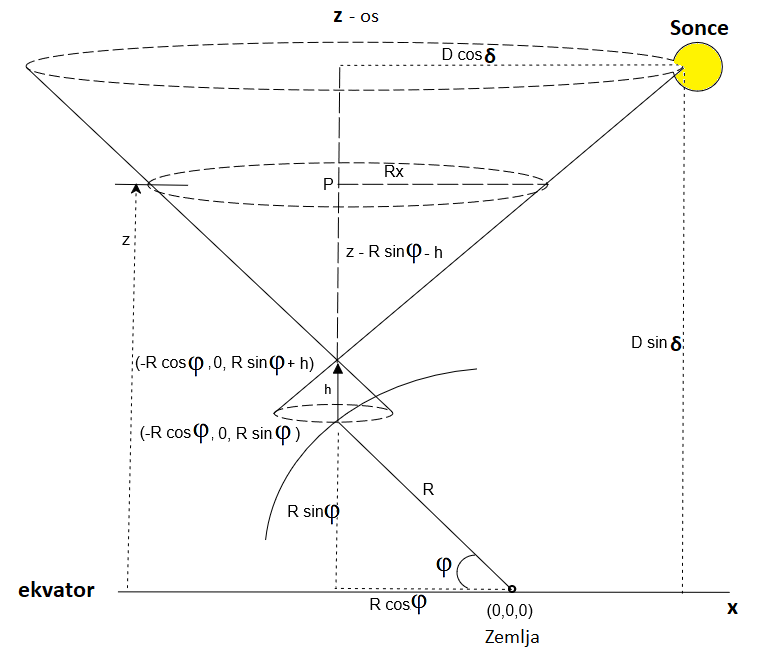
Sončna ura 4
Zdaj moramo najti enačbo stožca, ki ga tvorijo
Sončni žarki na konici palice v obhodu enega dneva (slika levo). Koordinate (0, 0, 0) so v središču Zemlje.
Povejmo še, da je
ravnina pod palico kar ravnina našega obzorja, ki se dotika Zemlje na vbodišču palice (slika desno).
Torej črta, ki povezuje središče Zemlje
in točko preboda palice s tlemi, je kar normalna na to
ravnino. Iz tega je mogoče najti enotski vektor, ki je kar normala na ravnino
[ n = r/|r| = (-R cosφ, 0, R sinφ)/R = (-cosφ, 0, sinφ) ].
Poleg tega ta ravnina poteka skozi koordinate vboda
palice ro = (-R cosφ, 0, R sinφ ),
y os kaže v ravnino. Pozneje bomo to ravnino našega obzorja obravnavali posebej in
na njej poiskali presek s stožcem sence palice.
Obravnavajmo točko P na višini 'z' od
središča Zemlje. Koordinate takšne točke so (-Rcosφ, 0, z).
Polmer kroga osnovne ploskve stožca na tej
višini je 'Rx' v središčni točki P z že omenjenimi koordinatami (-Rcosφ, 0, z).
Tako je enačba kroga osnovne površine podana kot:
(x+Rcosφ)2
+ y2 = Rx2
Sončna ura 5
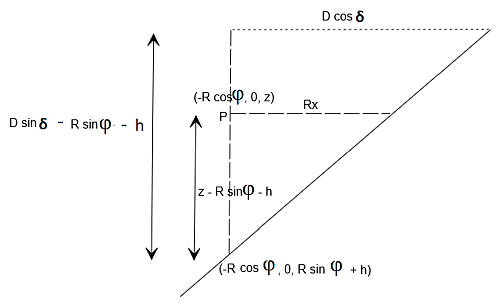
Zdaj bomo poiskali izraz za "Rx".
Na zgornji sliki obravnavajmo manjši pravokotni trikotnik z osnovo 'Rx'
in višino ‘z – R sinφ – h’ in podobno (večji)
trikotnik z osnovo 'D cosδ' in višino 'D sinδ – R sinφ
– h’. Iz podobnih trikotnikov veljajo naslednja razmerja:
Rx/(Dcosδ) = (z-R sinφ-h)/(Dsinδ-Rsinφ-h)
Rx/(Dcosδ) = (z-R sinφ-h)/(D(sinδ- Rsinφ/D-h/D))
Ker je D >> R in tudi D >>> h, velja:
Rx = cosδ(z - R sinφ-h)/sinδ
Rx = (z - Rsinφ - h)/tanδ
Enačba stožca (osnovne površine, preseka z ravnino) ima sedaj obliko:
((x+Rcosφ)2 + y2)tanδ2 = (z-R sinφ-h)2
To je enačba stožca (osnovne krožne površine), oblikovanega na konici palice
višine 'h', ki je usmerjen vzdolž zemeljske osi
vrtenje. Zagotovo velja, če ravnina obzorja (ki poteka skozi osnovo
palice) preseka stožec, bo senca sledila stožcu - stožnici. Ta
stožčasti prerez je torej pot, ki jo zariše senca palice.
Spodnja slika prikazuje ravnino obzorja in stožec,
ki ga nariše senca palice na horizontalni ravnini.
Sončna ura 6
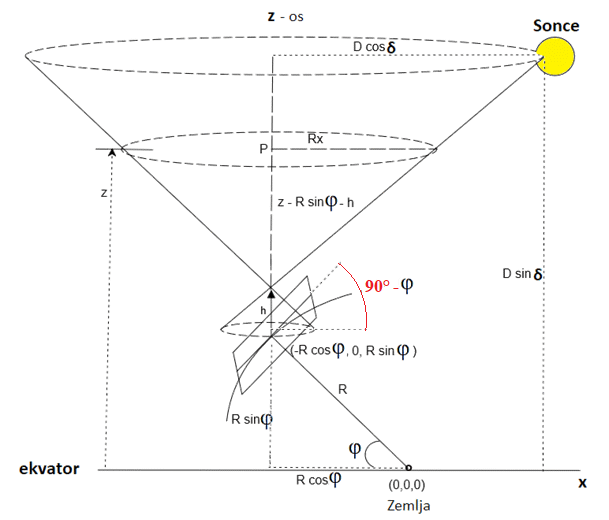
Ravnina pod palico je kar ravnina obzorja, ki se dotika Zemlje na vbodišču.
Torej črta, ki povezuje središče Zemlje
in točko preboda palice s tlemi, je kar normalna na to
ravnino. Iz tega je mogoče najti enotski vektor, ki je kar normala na ravnino
[ n = r/|r| = (-R cosφ, 0, R sinφ)/R = (-cosφ, 0, sinφ) ].
Poleg tega ta ravnina poteka skozi koordinate vboda palice ro = (-R cosφ, 0, R sinφ ),
y os kaže v ravnino.
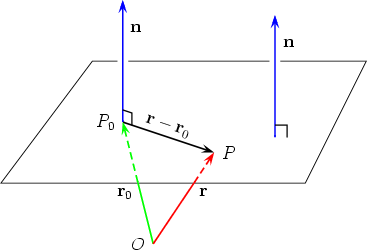
Zato je enačba takšne ravnine kar skalarni produkta med normalo n in premico na ravnini, izraženo z razliko vektorjev
(r - ro), kjer je ro vektor do ravnine (v našem primeru je ro
pravokoten na ravnino, torej na horizont, saj je kar polmer Zemlje R).
Skalarni produkt je zaradi pravokotnosti enak nič. Zato velja:
n·(r - ro) = 0,
kjer je n = (cosφ, 0, sinφ), vektor r = (x, y, z) in
ro = (-R cosφ, 0, R sinφ).
Tako velja: (-cosφ, 0, sinφ)·( (x, y, z) - (-R cosφ, 0, Rsinφ) ) = 0
Izvedemo odštevanje in še skalarnoi produkt, tako dobimo:
(-cosφ, 0, sinφ)·(x + R cosφ, 0, z - Rsinφ) = 0
-x cosφ - R cosφ2 + 0 + z sinφ - R sinφ2 = 0
-x cosφ + z sinφ - R(cosφ2 + sinφ2) = 0
Tako zapišemo končno obliko enačbe naše iskane horizontalne ravnine:
-x cos φ + z sin φ = R
Gre torej za rotacijo (okrog y osi) koordinatnega sistema za kot (90 - φ) iz ekvatorske v tangentno ravnino.
Do tukaj smo sledili izpeljavi na strani
"https://amateurastroblog.wordpress.com/2016/06/26/the-mathematics-of-shadows-and-time-keeping-by-sundials/
,
ki pa ima od tu naprej napako
- ker so žal napačno upoštevali rotacijo ravnine.
Vstavili so enačbo nove ravnine in ne
s preslikavo koordinat zarotiranih ravnin.
Njihova izpeljava žal vrne napačne krivulje, dolžine senc !!! Izpeljava se začne sicer odlično, nazorno, potem
pa spregledajo znano matematično resnico, da rotacija ni translacija :(
Zgornja izpeljava enačbe naše ravnine horizonta je bila tako tudi na nek način odvečen korak.
A nič hudega - tako si lahko vsaj nekoliko lažje predstavljamo, kako prehajamo iz ene ravnine v drugo na
dimenzijah Zemlje in Sončevega sistema.
Poglejmo matematično korektno pot za transformacijo koordinat med dvema zarotiranima
kartezičnima koordinatnima sistemoma.
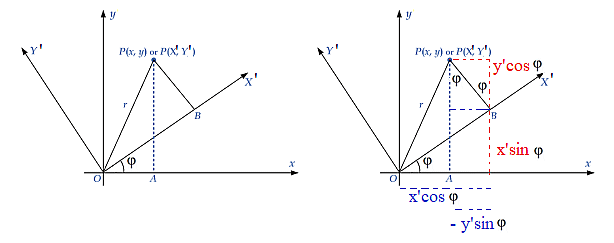
Slika zgoraj, koordinatni sistem (') je zarotiran za kot φ glede na horizontalo.
Preslikava je znana in velja (pomagajte si s slikama):
x = x'cos (φ) - y' sin (φ)
y = x'sin (φ) + y' cos (φ)
z = z'
Vse kar potrebujemo zdaj je, da zamenjamo vrednost z in x v zgornji enačbi stožca,
pridobljeni prej, da bi tako našli pot
sence palice čez celoten dan na horizontalni (tangentni) ravnini opazovalca,
ko je Sončna deklinacija 'δ'.
Toda te enačbe je mogoče še poenostaviti,
če bazo prevedemo na vbodišče palice
(-R cosφ, 0, R sinφ ).
V tem primeru naj bodo nove koordinate
X, Y, Z . Potem velja:
X = x + Rcosφ, Y = y, Z = z - Rsinφ
in stare koordinate lahko zapišemo kot:
x = X - Rcosφ,
y = Y, z = Z + Rsinφ
Enačba stožca se sedaj poenostavi kot:
(X2 + Y2)tanδ2 = (Z - h)2
Enačba ravnine se poenostavi na:
-cos φ X + sin φ Z = 0
Velja torej tudi iz zgornje enačbe:
Z = Xcos φ/sin φ = X/tan φ
Zadnjo povezavo za (Z) so vstavili kar v (X2 + Y2)tanδ2 = (Z - h)2 ) in tako
dobili napačno formulo
[ (X2 + Y2)tanδ2 = ((cos φ/sin φ)X - h)2 ],
to napako najdete na strani:
https://amateurastroblog.wordpress.com/2016/06/26/the-mathematics-of-shadows-and-time-keeping-by-sundials/
:(
S to rokohitrsko potezo so tako pozabili na pravilno pot, to je rotacijsko transformacijo !!!!!!!!!!!!!!!!!!!!!!!
Za naš primer pa torej velja, da rotiramo okrog y osi in da je kot rotacije (90 - φ) - glejte sliko tangente na Zemljo zgoraj.
Rotiramo torej x in z os, zato velja.
X = x'cos (90 - φ) - z' sin (90 - φ) = x'sin φ - z' cos φ
Z = x'sin (90 - φ) + z' cos (90 - φ) = x'cos φ + z' sin φ
Y = y'
Da bo manj pisanja, postavimo višino palice na h = 0 (stožec se dotika tal)
in bomo koordinato z zamaknili na koncu za z'=-v (navpična palica
na horizontali). Pri palici dolžine h, ki kaže proti polu, pa bomo naredili ustrezen x-zamik
(takrat velja za koordinati palice v = hy = h sin φ
in hx = h cos φ).
Zamenjajmo torej v (X2 + Y2)tanδ2 = (Z)2
spremenljivke iz že zapisane preslikave za rotacijo:
X = x'sin φ - z' cos φ
Z = x'cos φ + z' sin φ
Y = y'
Tako dobimo naslednji izraz:
((x'sin φ - z' cos φ)2 + y'2)tanδ2 = (x'cos φ + z' sin φ)2
Končni izraz za vertikalno palico dolžine z = -v je torej kar (odpravimo še črtice x',y',z' => x, y, z):
((xsin φ + v cos φ)2 + y2)tanδ2 = (xcos φ - v sin φ)2
Zgornji zapis je torej enačba poti, ki ji sledi
senca palice višine 'v', usmerjena navpično na Zemljini ravnini, horizontu.
Pri palici dolžine h, ki kaže proti polu, pa bomo naredili ustrezen x-zamik
(takrat velja za koordinati palice v = hy = h sin φ
in hx = h cos φ).
(( (x - h cos φ)sin φ + h sin φ cos φ)2 + y2)tanδ2 = ( (x - h cos φ)cos φ - h sin φ sin φ)2
Zgornji izraz pa je torej enačba poti, ki ji sledi
senca palice višine 'h', usmerjena vzdolž Zemljine
osi. To enačbo smo tudi iskali.
Enačba predstavlja stožčasti prerez.
Ta izpeljava je na spletu trenutno unikum - temelji pa žal na napačnem rezultatu iz strani
https://amateurastroblog.wordpress.com/2016/06/26/the-mathematics-of-shadows-and-time-keeping-by-sundials/.
Zmotili so se pri rotaciji ravnine, kjer so v enačbo ekvatorialne ravnine napačno
kar vstavili enačbo horizontalne ravnine, kar pa je pri rotaciji ravnine matematično napačna pot
(še zmeraj se dobi recimo hiperbolo, a njene vrednosti se ne ujemajo s potjo sence).
Pravilna je uporaba enačb transformacije koordinat pri rotaciji koordinatnega sistema.
In to sem tudi izvedel v zgornjih korakih. Omenjeno stran sem obvestil o napaki ...
sledi pa še klasična enačba poti, ki ji sledi
senca vertikalne palice višine 'v', ki je pokončno zapičena na horizontalno ravnino in seveda da enak rezultat
kot zgornji 2 enačbi - a njena izpeljava je bila izvedena preko klasične poti, to je
skalarnega produkta krajevnega vektorja na stožcu "r" in osi stožca "ro", glejte stran spodnje izpeljave
"pot_sence_sonca_zv_vert_pal.html".
Obe izpeljavi sta legitimni in seveda vrneta enak rezultat gibanja sence palice, to bomo preverili
v nadaljevanju. Sedaj pa še obljubljena klasična enačba:
(x2 + y2 + v2)sin2δ = (x cos φ - v sin φ)2
- to je klasična oblika enačbe sence palice zaradi dnevne poti Sonca
Obe enačbi sta v bistvu enaki, le pot do njiju je rahlo drugačna - pa povedano še dokažimo.
Spodnjo (v modri barvi) alternativno enačbo rahlo preoblikujmo in sicer izrazimo iz nje y2 in upoštevajmo,
da je:
1/tan2δ = cos2δ/sin2δ =
(1 - sin2δ)/sin2δ = 1/sin2δ - 1 .
((xsin φ + v cos φ)2 + y2)tan2δ = (xcos φ - v sin φ)2
Iz zgornjega zapisa torej izrazimo y2:
y2
= (xcos φ - v sin φ)2/tan2δ - (xsin φ + v cos φ)2
Sedaj upoštevajmo, da je 1/tan2δ = 1/sin2δ - 1.
Tako dobimo naslednji izraz:
y2 = (xcos φ - v sin φ)2(1/sin2δ - 1) - (xsin φ + v cos φ)2
Ostane nam še množenje in kvadriranje, ter upoštevanje kotnih funkcij
[ sin2δ + cos2δ = 1]. Pa začnimo:
y2 = (xcos φ - v sin φ)2/sin2δ - (xcos φ - v sin φ)2 - (xsin φ + v cos φ)2
y2 = (xcos φ - v sin φ)2/sin2δ - (x2cos2φ - 2vx cos φsinφ + v2sin2φ)
- (x2sin2φ + 2vx cos φsinφ + v2cos2φ)
V zgornji enačbi opazimo, da se člena 2vx cos φsinφ odštejeta in da velja:
-x2cos2φ - x2sin2φ = -x2
in
-v2cos2φ - v2sin2φ = -v2
Tako dobimo obliko:
y2 = (xcos φ - v sin φ)2/sin2δ - x2 -v2
Če prenesemo x2 in v2 na levo stran in pomnožimo enačbo z sin2δ,
dobimo klasično obliko enačbe:
(x2 + y2 + v2)sin2δ = (x cos φ - v sin φ)2
Dokaz je tako končan. Katera izpeljava vam je ljubša? Ta - z rotacijo ravnine -
ali klasična s skalarnim produktom?
Morebiti je ta z rotacijo ravnine bolj razumljiva in predstavljiva. Obe skupaj pa
sta celota in sta izjemno poučni vaji za razumevanje postulatov matematike, geometrije.
Preprosta risba na
spletnem risalniku 'desmos'
potrjuje povedano za obe izpeljavi.
Not vstavimo enačbe:
a) alternativa izpeljava zgoraj za vertikalno palico:
\left(\ \left(x\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\ +5\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\right)\tan\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
b) klasična izpeljana enačba za vertikalno enačbo palice, ki vrne seveda enake rezultate kot opcija a:
\left(\ \left(\ 5\right)^{2}\ +x^{2}\ +\ y^{2}\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(x\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
c) alternativa izpeljava (z rotacijo) zgoraj za palico usmerjeno v smeri osi rotacije Zemlje, nebesne krogle -
da enak rezultat kot opcije d:
\left(\ \left(\left(x-5\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\ +5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\right)\tan\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(\left(x-5\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
d) klasična izpeljava za palico usmerjeno v smeri osi rotacije Zemlje dolžine h,
da enak rezultat kot opcija c
:
\left(\ \ \left(x-5\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\ +\ y^{2}\ +\ \left(5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}\right)\sin\left(23.44\cdot\frac{\pi}{180}\right)^{2}\ =\ \left(\left(x-5\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\right)\cdot\cos\left(46\cdot\frac{\pi}{180}\right)\ -5\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\cdot\sin\left(46\cdot\frac{\pi}{180}\right)\right)^{2}
Priporočam tudi 3D spletni risalnik
'desmos 3D' - https://www.desmos.com/3d
[osnova za risanje stožca je recimo
y^2+(z-5)^2=f(x)^2
ali
y^2+x^2=f(z-5)^2, klikneš še na opcijo add slider [f] ]
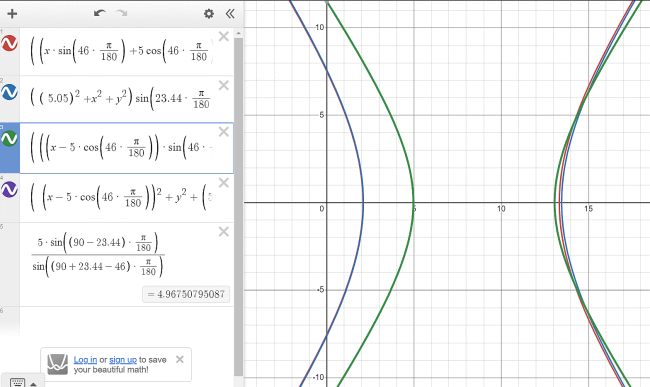
Grafi poti senc na poletni solsticij (δ=23.44°) za geografsko širino φ = 46 °:
a) (rdeča krivulja)
za izpeljavo, ki smo jo naredili tukaj (z rotacijo), vertikalna palica višine v = z = - 5 cm:
((xsin φ + v cos φ)2 + y2)tanδ2 = (xcos φ - v sin φ)2
b) (modra krivulja) za klasično enačbo (grafa sta enaka - da ju rahlo razločimo, je na grafu b palica rahlo podaljšana na 5.05 cm, desno
krilo hiperbole se tako rahlo razloči - modra in rdeča krivulja sta blizu skupaj)
(x2 + y2 + v2)sin2δ = (x cos φ - v sin φ)2
- a in b grafa tečeta enako
c) (modra krivulja) za poševno palico h = 5 cm pod kotom 46 ° usmerjeno proti polu nebesne rotacije
(za alternativno enačbo izpeljano z rotacijo):
(( (x - h cos φ)sin φ + h sin φ cos φ)2 + y2)tanδ2 = ( (x - h cos φ)cos φ - h sin φ sin φ)2
d) enaki pogoji, kot pri poševni palici c, le da za klasično izpeljavo (je skrita pod zeleno krivuljo):
((x - h cos φ)2 + y2 + (h sin φ)2)sin2δ = ((x - h cos φ) cos φ - h sin φ sin φ)2
Za palico
na polu φ=90° bo senca sledila krožni poti in
ob enakonočju (22. september in 21. marec, ko je δ=0°, senca
izriše ravno črto.
Spodaj je napačni graf za napačno formulo
[ (X2 + Y2)tanδ2 = ((cos φ/sin φ)X - h)2 ]
iz strani:
https://amateurastroblog.wordpress.com/2016/06/26/the-mathematics-of-shadows-and-time-keeping-by-sundials/
Za φ=45,777° (Clermont Ferrand Francija), δ=23,43°
(21. junij, poletni solsticij) je pot sence hiperbola - a napačna:(
sončna ura 7
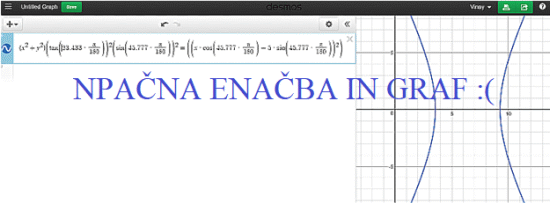
Zgoraj sta napačna enačba in graf, napaka je na strani:
https://amateurastroblog.wordpress.com/2016/06/26/the-mathematics-of-shadows-and-time-keeping-by-sundials/
3. Merjenje časa s Sončno uro
Spomnimo se, kako senca
palice na severnem tečaju sledi krožni poti
na vodoravni ravnini. Ravnina obzorja na severnem polu je
vzporedna z ekvatorjem. Na kateri koli zemljepisni širini 'φ', če
palico poravnamo vzdolž zemeljske osi (tj
kaže proti severu in tvori kot z vodoravno ravnino, ki je enak zemljepisni širini)
in sledimo senci na vzporedni ravnini
z ekvatorjem (takšna ravnina bo pravokotna na palico)
potem bomo videli, da senca sledi popolnoma krožni poti.
To je koncept ekvatorialnih Sončnih ur.
sončna ura 8
Ekvatorialna Sončna ura pri pomorščakovem spomeniku,
Port Arthur, Teksas, ZDA (geografska širina 29°52). Palica oklepa kot
29°52 z vodoravnico in kaže proti severu
Slika je vzeta iz: http://www.wsanford.com/~wsanford/exo/sundials/stpete/
Palica se imenuje tudi "gnomon". Z vodoravno ravnino oklepa kot
enak lokalni zemljepisni širini in je usmerjena
proti pravemu severu.
Zemlja se zavrti okoli svoje osi glede na Sonce v 24 urah,
torej ima kotno hitrost 360°/24 h [stopinj na uro] oz.
15° na uro. Za nas opazovalce, ki rotiramo vzdolž Zemlje,
se zdi, da se Sonce po nebu giblje s kotno hitrostjo 15°
na uro. Z drugimi besedami, Sonce se premakne za 15° v 1 uri
na nebu. To pomeni, da se bo senca na ekvatorialni številčnici
(kot je zgoraj) premaknila za 15° v eni uri.
Na podlagi tega preprostega sklepanja so črte, ki označujejo ure,
tudi narisane na ekvatorialni
številčnici. Toda ena uganka še vedno ostaja in to je: kako
oštevilčiti te ure, kako bi vedeli, če je 6
popoldan ali ob 16 h ?
To težavo je mogoče rešiti z zavedanjem, da je
opoldne za dani kraj na Zemlji Sonce neposredno nad glavo
(natančneje, je na začetnem poldnevniku, na velikem krogu, ki poteka
skozi kraj/točko na Zemlji ter nebesni severni in južni pol).
Tako bo senca palice, usmerjene proti severu, opoldne kazala proti
sever. Zato so lahko urne črte na ekvatorialni Sončni uri
označeno kot je prikazano na sliki:
Sončna ura 9
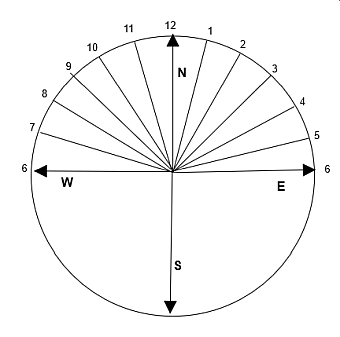
Črta, linija, ki kaže proti severu, se zgodi opoldne (12.00).
Ekvatorialne Sončne ure morajo biti označene na obeh straneh, saj pozimi
na eni strani ne bo nastala senca. To je zato,
ker gre Sonce južno od nebesnega ekvatorja (ali, ker Sončna deklinacija postane
negativno po enakonočju). Ugotovimo lahko, da so ekvatorialne Sončne ure lahko razumljive,
vendar jih je praktično težko narediti.
3.1 Horizontalne Sončne ure
V tej vrsti konfiguracije
je palični "gnomon" podoben ekvatorialni Sončni uri, usmerjen proti
severu in tvori kot, ki je enak lokalni zemljepisni širini z
vodoravna ravnina. V tej konfiguraciji se senci sledi na vodoravni
ravnini.
Trik tukaj je najti urne črte. Da bi
poiščite urne premice si lahko predstavljamo ekvatorialno Sončno uro z urnim kotom
‘E’= 15° (kot med dvema urnima črtama) in projiciramo krožnico
ravnina te številčnice na vodoravni ravnini ob ‘gnomonu’ oz
palici.
sončna ura 10
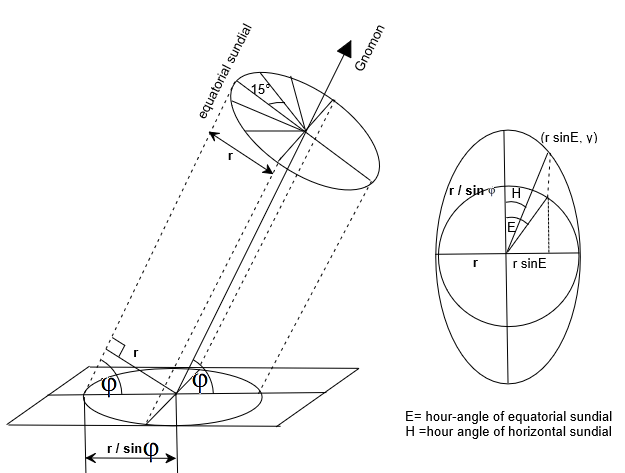
Projekcija kroga na vodoravno ravnino je
elipsa (lahko se dokaže). Zapišimo enačbo elipse:
x2/a2 + y2/b2 = 1
Kot izjemo, v tej orientaciji elipse zamenjamo pomen konstant a in b, naj bo torej
v tem primeru b glavna os elipse in a mala - zgolj za naš primer.
Naj bo polmer številčnice "ekvatorialne Sončne ure"
'r'. Iz slike (levo) razberemo, da je mala os 'a' = r in
glavna os elipse oklepa kot φ s polmerom 'r' in zato velja:
b = r/sinφ
- zadnji izraz nadomestimo v enačbi elipse:
x2/r2 + (y2/r2)sinφ2 = 1
Na sliki zgoraj desno je urna črta na ekvatorialni številčnici pod kotom
od V (=15°) do črte sever-jug (ali črte opoldanske ure).
Koordinate ustrezne projekcije urnega kazalca na elipso lahko
dobimo kot: (r sinE, y). Zamenjava v enačbi elipse:
(r2 sinE2)/r2 + (y2/r2)sinφ2 = 1
Rešitev zgornje enačbe za spremenljivko y je kar:
y = rcosE/sinφ
Koordinate urne oznake na vodoravni ravnini so tako:
(r sinE, y) = (rsinE, rcosE/sinφ)
Če pogledamo sliko zgoraj desno, potem velja za tan H = x/y = rsinE/y = rsinE/(rcosE/sinφ) = tanE sinφ,
- tako bo urni kot H na vodoravni ravnini kar:
H = tan-1 (tanE sinφ) = atan(tanE sinφ)
Kaj imamo sedaj na razpolago:
Za palico višina 'h' na zemljepisni širini φ, če palico usmerimo vzdolž
zemeljske osi (tj. pod kotom z vodoravno ravnino,
ki je enaka zemljepisni širini φ in kaže proti severu), velja.
Znamo risati urne črte na vodoravno
ravnino in kako označimo te črte.
H = atan(tanE sinφ), kjer je E=15°
mi pa iščemo enačbo poti, ki jo izriše senca gnomona
na določen dan.
(X2 + Y2)tanδ2 sinφ2 = (cos φ X - h sinφ)2
Na poletni solsticij 21. junija je deklinacija Sonca 'δ'=23,43°. Zmanjšuje se skoraj linearno
do 21. decembra, ko je δ=-23,43°. Nato začne spet skoraj linearno naraščati
do 21. junija, ko je δ=23,43°. Zemlja potuje okrog skupnega težišča s Soncem
po elipsi - kar pomeni,
da se sončna deklinacija skozi leto ne spreminja linearno. Spreminja se cca s
sinusno funkcijo -
deklinacijski kot se tako lahko natančneje izračuna z enačbo
δ =
arcsin[ sin( - 23.436° ) · cos ( ( N + 10 )360°/365.24 + (360°/π)0.0167 sin( ( N - 2 )360°/365.24 ) ) ]
N je število dni od polnoči UT, ko se začne 1. januar
(tj. dnevi rednega datuma -1) in lahko vključuje decimalke za prilagoditev z lokalnim časom
pozneje ali prej v dnevu. Število 2 v (N-2) je približno število dni po 1. januarju do perihelija Zemlje.
Število 0,0167 je trenutna vrednost ekscentričnosti Zemljine orbite.
Največje napake v tej enačbi so manjše od ± 0,2°.
Linearnost je le približek,
ko zanemarimo napako, ki jo povzroča majhna ekscentričnost zemeljske orbite.
Zato je, če privzamemo linearnost, za vse deklinacijske kote za vse
dni v letu mogoče dobiti s preprosto linearno interpolacijo. A bolje je uporabiti zgornjo enačbo.
Tako lahko narišemo enačbe
poti, ki jo zariše senca ob vseh datumih
leta. Zato lahko ocenimo tudi datume.
4. Poglejmo, kako ta trditev deluje:
Z uporabo enačbe H = atan(tanE sinφ) poiščemo urne kote
Recimo za geografsko širino 45.777 so podatki za E° in H° naslednji:
E° H°
15 10.869
30 22.477
45 35.626
60 51.143
75 69.499
90 90.000
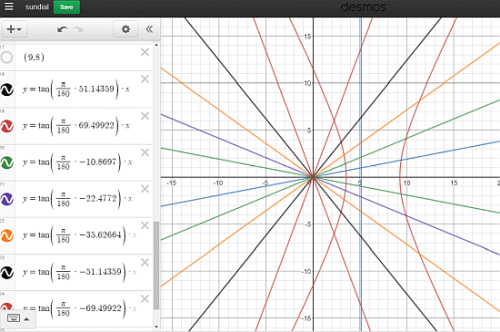
Sončna ura 11
Za risanje urnih črt se lahko uporabi spletni risalnik
"desmos".
Upoštevajoč črto za os x kot opoldan (12 pm), potem je
enačba za 11:00 uro kar y=tan (10,869).x in za 13:00 uro
kar y=tan (-10,869).x in tako naprej.
Tudi za izračun poti sence po datumih in za risanje grafa se uporabi enačbo:
(X2 + Y2)tanδ2 sinφ2 = (cos φ X - hsinφ)2.
sončna ura 12
Sončna ura 13
Primer Sončne ure ali gnomona na zgornji sliki. Stranica višine 'h=5cm' je usmerjena
proti severu pod kotom 45,7° (geografska širina Clermont-Ferrand) z
vodoravno ravnino. Z drugimi besedami, ta stran gnomona je poravnana z
zemeljsko osjo vrtenja (za pomanjšanje Sončne ure se recimo
vse dimenzije deli s faktorjem 2, potem je višina
gnomona je 2,5 cm).
Povezava
Observations (Contd..The mathematics of shadows and time-keeping by sundials) vsebuje opažanja in težave z
merjenjem časa s Sončnimi urami.
Do napake, ki je zgoraj odpravljena, delno povzeto po:
https://amateurastroblog.wordpress.com/2016/06/26/the-mathematics-of-shadows-and-time-keeping-by-sundials/
Povzel in dodal popravke
Z. Vičar (24. dec. 2024)
