Ugotavljanje lomnega količnika materiala po lomu žarkov na planparalelnih stranicah prozornega kvadra in merjenje mejnega kota popolnega odboja.
Pripomočki:
· prozoren kvader
· cilindrični polkrožni element
· svetilo
· usmernik
· zaslonka
· kotomerni krog
Na papir položimo kvader in narišemo njegov obris. Žarek svetlobe usmerimo poševno na stranico kvadra. S svinčnikom označimo po sredi žarka več točk, da lahko narišemo smer svetlobe pred vstopom v kvader in po izstopu. Povežemo točki vstopa in izstopa, da dobimo pot žarka skozi kvader. Postopek ponovimo še pri štirih drugih naklonih vstopajočega žarka.
Vstopni in izstopni žarek sta vzporedno premaknjena. Narišemo vpadne pravokotnice in izmerimo vpadne in lomne kote. Po enačbi
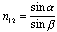
izračunamo lomni količnik, iz vseh meritev pa še njegovo povprečno vrednost.
Za paralelni premik žarka velja enačba:
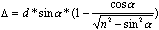
kjer je d debelina plošče, a pa vpadni kot. Izmerimo potrebne količine, iz enačbe izrazimo lomni količnik n in ga primerjmo z vrednostjo, ki smo jo izračunali z lomnim zakonom.

Do popolnega odboja svetlobe pride, ko svetloba prehaja iz optično gostejše snovi v optično redkejšo. Za lomni kot popolnega odboja velja:
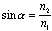
kjer je n2 lomni količnik zraka (1,00), n1 pa lomni količnik cilindričnega polkrožnega elementa. Položimo cilinder na sredo kotomernega kroga in izmerimo kot, pri katerem pride do popolnega odboja svetlobe. Meritev še nekajkrat ponovimo in izračunamo povprečno vrednost lomnega količnika.
Optična prizma:
Z risanjem določi lomni kot prizme in določi lomni količnik stekla, iz katerega je prizma.
Stekleno prizmo postavi na risalni list. Na papir začrtaj meje prizme, nato zabodi dve buciki (1 in 2) na eno stran prizme. Poglej z druge strani prizme tako, da vidiš skozi prizmo obe buciki. Z viziranjem zabodi buciko 3 na mejo (drugo stran) prizme in buciko 4 tako, da sta z bucikama 1 in 2 navidezno na isti premici.
Na papirju začrtaj prehod žarka po bucikah in s kotomerom izmeri lomni kot prizme. Izvedi račun za lomni količnik stekla:
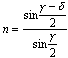
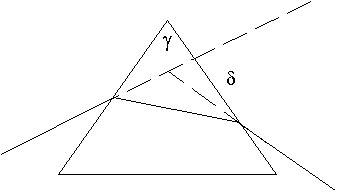
(iz: http://baza.svarog.org/fizika/maturitetne_naloge/18_lom.php)
Zbiralna (konveksna)


Naj bo a > f.
Slika predmeta je obrnjena in realna, saj sliko lahko projeciramo na platno ali film, lahko pa jo tudi opazujemo skozi drugo lečo (lupo) in tako ustvarimo teleskop ali mikroskop.
Slika 1.1
Za izračun razmerja med velikostjo predmeta in slike, razdalje (a) predmeta od optične ravnine in razdalje (b) slike od predmeta zadostujeta dva žarka.
Žarek 1 potuje od konice predmeta k leči vzporedno z optično osjo.
Žarek 2 potuje od konice predmeta k leči skozi geometrijsko središče.
F -gorišče leče
f -goriščna razdalja leče
Poiščimo povezave med a, b, p, s in f s pomočjo podobnih trikotnikov (slika 1.1).
1.1)  1.2)
1.2) 
Če enačbi med sabo delimo in nekoliko preoblikujemo, dobimo enačbo 3, ki ji tudi pravimo enačba zbiralne leče (v našem primeru je a > f).
deljenje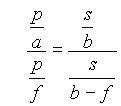 sledi
sledi
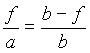 sledi
sledi 
1.3
)
Če je razdalja (a) do predmeta zelo velika, potem približno velja: 1/a=0 ,kar pomeni, da slika nastane zelo blizu gorišča, brez velike napake velja: b=f
Kje torej nastane slika objektiva teleskopa in zakaj?
2. Zbiralna leča kot lupa (a<f)

Slika 2.1
V primeru, da je razdalja predmeta (a) od optične ravnine leče manjša kot goriščna razdalja (f), nastane povečana, pokončna in navidezna slika predmeta na isti strani kot je pred
met. Lahko bi tudi rekli, da je razdalja b negativna.Izpeljimo povezave med a, b, p, s in f s pomočjo podobnih trikotnikov (slika 2.1).
2.1)  2.2)
2.2) 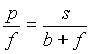
Če enačbi med sabo delimo in nekoliko preoblikujemo, dobimo enačbo 3, ki ji tudi pravimo enačba zbiralne leče (v našem primeru je a > f).
deljenje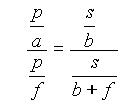 sledi
f/a=(b+f)/b sledi
sledi
f/a=(b+f)/b sledi 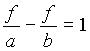
2.3
) ali
ali

Enačba je zelo podobna enačbi zbiralne leče, če je a>f, le da je sedaj razdalja b negativna.
3. Fotoaparat, diaprojektor, lupa (okular), teleskop
in definicije povečav
3.1. Fotoaparat
Fotoaparat je optično-mehanični sistem, ki predmete preslika na film. Slika na filmu je obrnjena, realna in ponavadi pomanjšana. Fotoaparat je sestavljen iz objektiva (slika 3.1), kateri projecira svetlobo odbito ali emitirano od realnih predmetov na film in časovnega mehanizma za proženje, ka
teri odmakne zaveso pred filmom, da se le ta osvetli.Objektiv je sistem leč z vgrajeno spremenljivo vhodno odprtino, ki odloča o zaslonki. Zaslonka je razmerje (kvocient) med goriščno razdaljo (f) in vhodno odprtino (D), velja: zaslonka=f/D (vrednosti so ponavadi od 2,8 do 22, za šolski teleskop LX200 je to razmerje 2500mm/250mm=10). Manjša je vrednost zaslonke, večji je premer vhodne odprtine D, več svetlobe pade na film, film je bolj osvetljen in obratno. Razmerje (kvocient) med vhodno odprtino (D) in goriščno razdaljo (f) je relativna odprtina: D/f. Relativna odprtina je tudi obratna vrednost zaslonke: 1/zaslonka=1/(f/D). Osvetlejnost filma je sorazmerna s kvadratom relativne odprtine (D/f)2=(1/(f/D))2.
Z vrtenjem objektiva ostrimo sliko, to je spreminjamo razdaljo b, ki je ponavadi le nekoliko večja od f, za zelo oddaljene predmete je razdalja b kar enaka f. Globinska ostrina se zelo poveča, če je vhodna odprtina zaprta (zaslonka 11 ali 16). V astronomiji potrebujemo odprtine velikih premerov, da ulovimo več prihajajoče svetlobe, ki je ponavadi šibka, ker so vesoljska telesa zelo daleč.Objektiv je, na kratko, zbiralna leča (sestavljena iz večih leč), kjer je a>f in veljajo enačbe na strani 1.
O povečavi težko govorimo, razen če fotoaparat montiramo na mikroskop. V splošnem si najraje predstavljamo, da je povečava definirana kot razmerje velikosti slike in predmeta, velja:
povečava je M=s/p, za vesoljska telesa je to kar f/a, kar pomeni, da je povečava (v tem primeru "pomanjšava") precej manjša od 1. Ugotovi odkod izraz M=f/a za veso
ljska telesa?---------
Opomba
Tak način definicije povečave (slika/predmet) ponavadi ni ustrezen. V splošnem je povečava definirana kot razmerje med tangensom zornega kota pod katerim vidimo telo s prostim očesom in tangensom zornega kota pod katerim vidimo telo skozi optični instrument.

Slika 3.1
3.2. Diaprojektor
Diaprojektor preslika predmet (ponavadi diapozitiv) na oddaljen zaslon, kjer dobimo obrnjeno močno povečano sliko predmeta. Diaprojektor je v grobem sestavljen iz žarnice, ki presvetli diapozitiv in objektiva (sestavljena zbiralna leča), ki presvetljeni diapozitiv projecira na zaslon (slika 3.2). To je obraten postopek kot pri fotografiranju, saj že posnet predmet na filmu povečamo s projekcijo na zaslon, kjer je projekcija lahko celo večja kot s
a m predmet v naravi. Z vrtenjem objektiva ostrimo sliko, to je spreminjamo razdaljo a, ki je ponavadi le nekoliko večja od f. Povečava diaprojektorja je spet definirana kot razmerje med velikostjo slike (slika na platnu) in predmeta (predmeta na diapozitivu): Md =s(na platnu)/p(na diapozitivu) in je tipično nekaj 10 kratna.Objektiv je sestavljena zbiralna leča, kjer je razdalja a le nekoliko večja od f in veljajo enačbe na strani 1.

Slika 3.2
3.3. Povečava Lupe
Lupa je zbiralna leča s kratko goriščno razdaljo, s katero predmet navidezno povečamo, tako da ga postavimo med optično ravnino in gorišče (a<f) ali v gorišče (a=f).
Poglejmo primer če (a<f)
Odmaknimo lupo toliko od predmeta, da navidezna povečana slika nastane na bližnji razdalji (xo=25cm) očesa. Bližnja razdalja očesa je razdalja, na kateri oko (človek) predmet najbolje vidi, oziro najbližja razdalja, ko še lahko brez naprezanja ostri sliko. V povprečju znaša bližnja razdalja xo=25cm. Iz te izkušnje izpeljimo povečavo, pomagajmo si s sliko 3.3.
Iz razmerja 2.2 (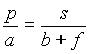 )
sledi,
da je po definiciji povečava
)
sledi,
da je po definiciji povečava
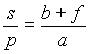 .
Ker je b+f približno enako xo
, in ker je razdalja a le
nekoliko krajša od f sledi, da je v grobem povečava lupe:
Ml=xo/f.
.
Ker je b+f približno enako xo
, in ker je razdalja a le
nekoliko krajša od f sledi, da je v grobem povečava lupe:
Ml=xo/f.
Primer: lupa z goriščno razdaljo f=2,5cm poveča M
l=25cm/2,5cm=10 krat.Poglejmo primer če (a=f)
Najlažje gledamo skozi lupo predmet v goriščni ravnini (a=f). Slika nastane v neskončnosti in oko prilagodimo na neskončnost. Velikost slike na očesni mrežnici je premosorazmerna tangensu zornega kota telesa (slika 3.3). Zorni kot je kot pod katerim vidimo telo. Povečavo optičnega instrumenta torej lahko tudi definiramo, kot razmerje med velikostjo slike, ki jo dobimo na mrežnici s pomočjo optičnega instrumenta, ter velikostjo slike
, ki jo vidi prosto oko. Ta definicija je splošno veljavna in nam da enak rezultat, glej spodnjo sliko. j 1 je kot pod katerim vidimo predmet skozi lupo, j 2 pa je kot pod katerim vidimo predmet s prostimi očmi na bližnji razdalji xo. Seveda je zorni kot j 1 večji od kota j 2, saj smo pri lupi predmet približali očesu na razdaljo blizu f, ki pa je manjša ali enaka xo. Velja:tg(j 2)=P/xo, tg(j 1)=P/a je približno P/f,
sledi že znani rezultat:
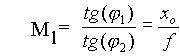 .
.

Slika 3.3
3.4. Teleskop
Teleskop je naprava, ki nam navidezno približa oddaljene predmete in zbere več svetlobe kot prosto oko, ker ima večjo vhodno odprtino in zato vidimo tudi manj svetle objekte v daljnem vesolju.
Obravnavali bomo le teleskop sestavljen iz sistema zbiralnih leč. Teleskop, ki je sestavljen izključno iz leč imenujemo tudi refraktor. Ime izhaja iz bistvenega pojava, da se svtloba (žarki) pri prehodu skozi leče lomi, temu pojavu pa s tujko rečemo tudi rafrakcija. Poznamo namreč tudi teleskope reflektorje, ki imajo kot objektiv vbočeno zrcalo, imenovano tudi konkavno zrcalo (amaterski teleskopi imajo ponavadi cenejše kroglno zrcalo, imenovano tudi sferno, profesionalni pa optično kvalitetnejše parabolično zrcalo). Take teleskope imenujemo zrcalne oziroma refleksne, ker je bistvena optična lastnot odboj, ki ga s tujko imenujemo refleksija. Zrcalni ali refleksni teleskopi imajo določene prednosti pred refraktorskimi. Pri zrcalnih teleskopih ni barvne napake, pa tudi vgradnja vecjih objektivov (tudi šestmeterskih zrcal) je mogoča. Pri lečnih (refraktorskih) objektivih pride, zaradi lastne teže in voskoznosti stekla, do omejitev na velikost enega metra. Optična geometrija in tudi osnovni zaključki so pri obeh tipih teleskopov enaki.Teleskop ref
raktor sestavljata objektiv, ki da realno sliko in lupa (okular), ki sliko objektiva še dodatno poveča. Kot zanimivost, Galilejo G. je kot okular uporabil razpršilno lečo, tak sistem da pokončno sliko, a manjše zorno polje.Zastavimo si nekaj vprašanj!
Na kateri razdalji tvori objektiv realno sliko?
Na kateri razdalji tvori okular navidezno sliko?
Objektiv teleskopa tvori sliko skorajda v gorišču (zakaj?). Kako izračunamo velikost slike, ki jo tvori objektiv, če poznamo goriščno razdaljo objektiva in zorni kot telesa? Če opazujemo vesoljsko telo, je zorni kot pod katerim ga vidimo ponavadi zelo majhen. Iz spodnje slike tako lahko razberemo, da je računanje velikosti slike, ki jo tvori objektiv, kar enako računanju loka na krogu. Razlaga!
Če je lok naprimer kar obseg kroga, potem velja: O=2p r=j r,j =kot, ki meri 2p radianov, to je 6,28radianov.
Torej je 2p radianov=360o, ali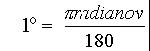 ;
;
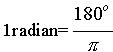 .
Ker je pri majhnih kotih tetiva skorajda enaka loku, je
naša trditev utemeljena, glej sliko 3.4.
.
Ker je pri majhnih kotih tetiva skorajda enaka loku, je
naša trditev utemeljena, glej sliko 3.4.
lok=jr
če j
<5o potem je tetiva približno enaka loku.Torej velja:
| S=j *f | -če zamenjamo lok s sliko (s) in r z goriščem (f) |
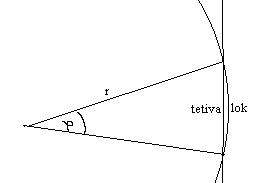

Slika 3.4
Primer:
Kot pod katerim vidimo Luno je j =30', goriščna razdalja objektiva (teleskopa) naj bo f=500mm. Kako velika slika nastane na filmu?
slune=j f
j pretvorimo v radiane (upoštevamo, da je 1o=60'): radianov
radianov
REZULTAT: s=4,4mm, kar je že solidna velikost.
Opomba: radianov ponavadi ne zapisujemo.
3.4.1
. Povečava teleskopaVelikost slike, ki jo tvori objektiv, je odvisna od razdalje predmeta od
optične ravnine (v našem primeru leži optična ravnina v leči), velikosti predmeta in seveda goriščne razdalje objektiva (fob). Če je predmet zelo daleč, kar je v vesolju zmeraj res, sta za določitev velikosti slike dovolj zorni kot, in goriščna razdalja objektiva. Zakaj? Povečava okularja (lupe) pa je odvisna od goriščne razdalje okularja (fok). Povečava teleskopa je torej odvisna od goriščnih razdalj objektiva in okularja. Povečavo teleskopa izrazimo kot kvocient med (fob) in (fok). Zakaj? Povečava teleskopa je: Mt=fob/fokČe pogledamo sliko 3.4.1, lahko uporabimo isto logiko kot pri lupi. Povečava okularja je kar kvocient med navidezno sliko okularja
(sok) in realno sliko objektiva (sob). Slika (sob), ki jo tvori objektiv, ima vlogo predmeta, ki ga z lupo (okularjem) povečamo. Poglejmo koliko prispevata k tej povečavi skupaj objektiv in okular.Po definiciji povečave lupe za okular velja: M
ok=Sok/Sob= xo/fok
Povečava teleskopa je seveda omejena zaradi "migetanja" zraka (maksimalno 500 krat) in ločljivosti teleskopa, ki je povezana z valovno dolžino svetlobe in vhodno odprtino teleskopa, na kateri se svetloba uklanja (ločljivost, najmanjši kot pod katerim še ločim dve telesi med sabo je a o=0,61*l /R in znaša za teleskop polmera 125 mm in valovno dolžino l =500 nm, 0,5 ločne sekunde ) . Groba ocena za povečavo, pri kateri še ni težav zaradi uklona svetlobe, je kar premer objektiva v mm. Torej, če je premer objektiva 100mm, pri povečavah okrog 100 še ne bo nobenih težav z ločljivostjo. Zakaj ima HST prednosti pred teleskopi na Zemlji?

Slika 3.4.1
============================================================
ZRCALA
Konkav
no (vbočeno) sferno (krogelno) zrcalo.
Animacijo je izdelal Tomaž Ščuka.
Izpeljava enačbe konkavnega zrcala je podana na k
oncu teksta. Enačba je enaka kot pri leči:1/f=1/a+1/b
Zrcala so zelo uporabna pri gradnji teleskopov, saj nimaj
o barvne napake in tudi lažje je ohranjati obliko zrcala, kot obliko velikih objektivnih leč. Sferična (krogelna) zrcala so zelo poceni in se na široko uporabljajo v amaterski astronomiji. Pri sferičnih zrcalih je problem napaka pasov (vsak pas glede na optično os ima drugačno gorišče), posledica česar je kavstika (glej spodnjo sliko).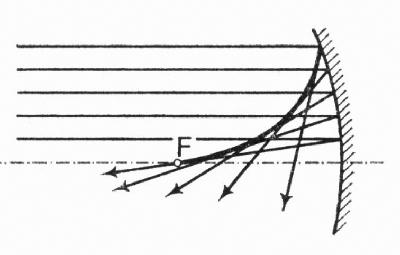
Pri sferičnih zrcalih je problem napaka pasov (vsak pas glede na optično os ima drugačno gorišče), posledica česar je kavstika.
Dva priljubljena primera zrcalnih teleskopov:


Geometrija konkavnega sferičnega zrcala

Barvna napaka in odprava napake

Barvna napaka pri lečah je posledica dejstva, da je lomni količnik
stekla različen za različne valovne dolžine, barve. Dokaz za tako napako je
že navadna prizma, ki razkloni belo svetlobo v barvni spekter, rdeča svetloba
se najmanj ukloni. To pomeni, da pripadajo
različnim barvam različne goriščne razdalje (oglej si enačbo tanke leče:
1/f=(n-1)(1/r1+1/r2)). Barvno napako odpravimo tako, da
leče sestavimo iz več leč (ponavadi iz dveh, achromatic doublet) z različnimi lomnimi
količniki in oblikami. Spodnja slika kaže primer odprave napake v sistemu
dveh prizem.
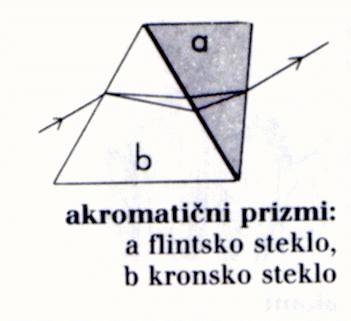
Rešitev problema barvne napake (akromatski objektiv iz dveh leč z različnima lomnima količnikom)
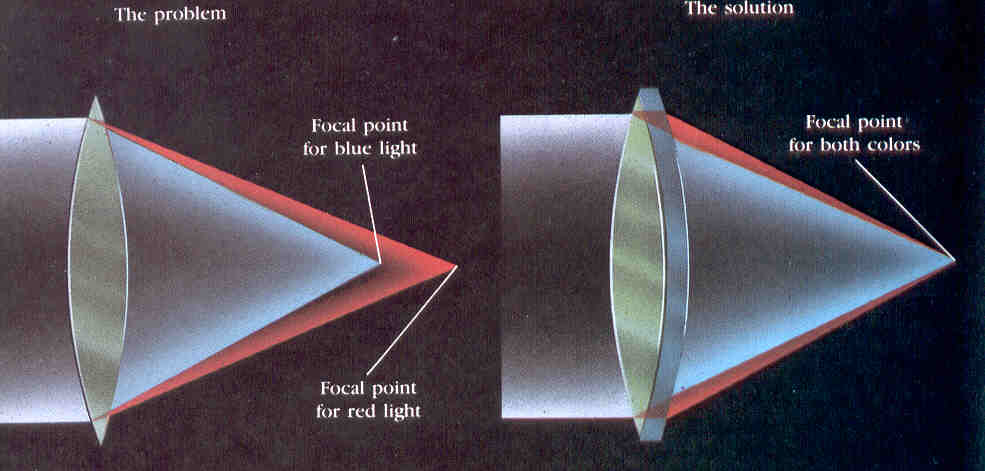
Oglej si tudi stran o teleskopih
Za astronomski krožek: ZORKO Vičar
Komentarji so zaželjeni.
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si
Nazaj na seminar.
Nazaj na domačo stran.


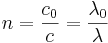 ,
,