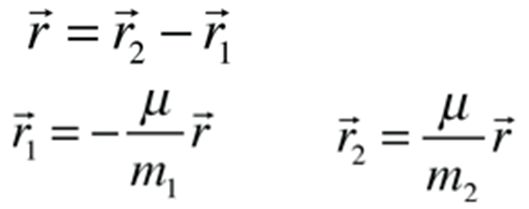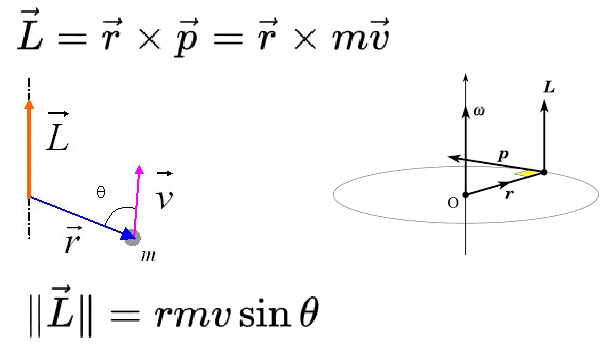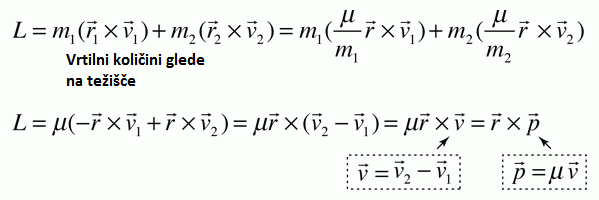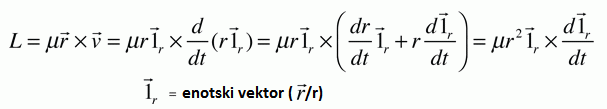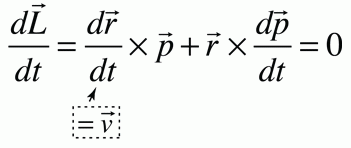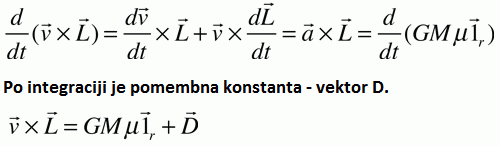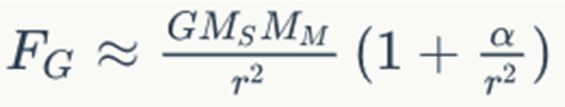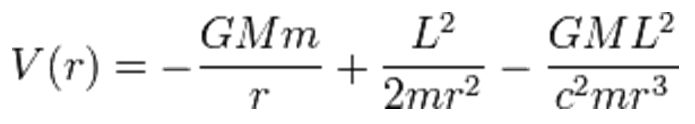Oblike orbit zaradi centralne sile sorazmerne z 1/r^2

Oblike orbit zaradi centralne sile sorazmerne z 1/r2


Za vajo dokažimo izpopolnjeno enačbo tretjega Keplerjevega zakona [ T2/a3 = 4π2/(G(m1+m2)) ]. Hkrati pa dokažimo, da centralna sila sorazmerna z 1/r2 (oz. obratno sorazmerna kvadratu razdalje), povzroči gibanje po stožnicah, in da se ploščinska hitrost planetov ohranja.

Predpostavimo orbito, recimo dveh zvezd na razdalji r = r1 + r2 (opazovani sistem sta torej samo ti dve zvezdi, brez zunanjih vplivov). Kjer je r1 razdalja od težišča sistema do zvezde z maso m1, r2 pa razdalja od težišča do zvezde z maso m2. Telesi potujeta okrog skupnega težišča.


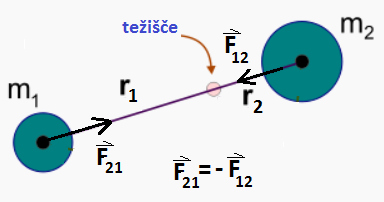
Medsebojno delovanje med dvema masama.

Razdalja med centroma mas je:
r = r1 + r2
Težišče je od centra m1 oddaljeno za r1:
r1 = rm2/(m1 + m2)
Gravitacijska sila je Fg = F21 = F12:
Fg = Gm1m2/r2
Reducirana masa je:
μ = m1m2/(m1 + m2)

Center mase m1 je od težišča sistema oddaljen za r1, m2 pa za r2. Veljajo pa naslednje povezave za izračun razdalj in težišča:
r = r1 + r2
r1m1 = r2m2 = (r-r1)m2
r1(m1 + m2) = rm2
r1 = rm2/(m1 + m2)
r1 = μr/m1 in r2 = μr/m2

Še vektorski zapisi:



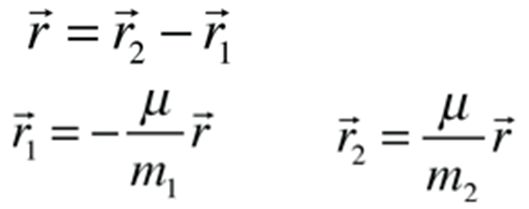
Kratka ponovitev vektorskega računa, z njim si bomo pomagali pri izpeljavah orbit nebesnih teles in nasploh pri razumevanju nebesne mehanike. Vektorski produkt je zapisan z znakom 'x', skalarni pa s piko '•'. Vektorji so v tekstu podčrtani ali imajo zgoraj puščico.

Slika prikazuje osnove vektorskega računa. Kartezične koordinate (različni vektorski zapisi, ko gre za vektorski račun, bo izraz poudarjen - "bold"):
r = (x, y, z)
Dolžina, velikost krajevnega vektorja r:
r = (x2 + y2 +z2)1/2
Skalarni produkt dveh vektorjev v ravnini je:
r1•r2 = (x1, y1)•(x2, y2) = x1y1 + x2y2 = |r1||r2|cos(φ)
Če sta vektorja pravokotna, je skalarni produkt 0, primer dveh takih vektorjev (x, 0) in (0, y):
(x, 0)•(0, y) =x0 +0y = 0
Slika prikazuje še vektorski produkt (axb), ki je spet vektor - a pravokoten na ravnino vektorjev a in b. Potem je še predstavljen zapis vektorjev v cilindričnih koordinatah in sferičnih koordinatah (pomemben za astronomijo - zvezde, planeti, lune so namreč v prvem približku sfere).




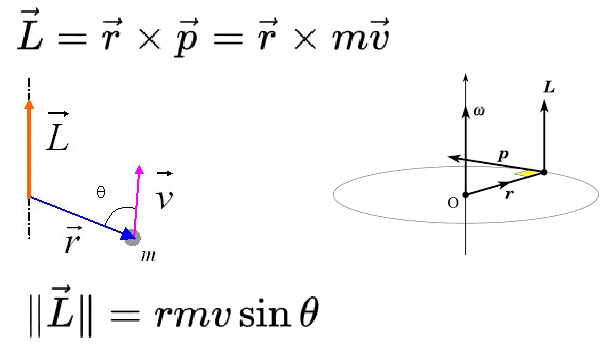
Vektorski zapisi so temelj fizike, z njimi zapišemo in računamo sile, navore, hitrosti, pospeške , poti, gibalne količine, vrtilne količine – primeri zgoraj. Kot vidimo je vrtilna količina L = rxp = m(rxv), po definiciji vrtilne količine kot vektorskega produkta med ročico in gibalno količino, pravokotna na ravnino kroženja – oz. poljubnega krivega gibanja. Da je vrtilna količina vektor, smo spoznali že kot otroci med igro pri precesiji vrtavke (enako se obnaša tudi rotirajoča Zemlja – kot ogromna vrtavka).

Vektorski produkt dveh vektorjev vrne vektor, ki je pravokoten na ravnino obeh. Velikost vektorskega produkta pa je enaka produktu velikosti obeh vektorjev in sinusa kota, ki ga vektorja oklepata. Tako je vektorski produkt vzporenih vektorjev, ki oklepata kot 0 °, enak 0 (saj velja sin(0°) = 0). Skalarni produkt dveh vektorjev zmeraj vrne skalar, ki je enak produktu velikosti obeh in cosinusa kota, ki ga vektorja oklepata. Tako je recimo skalarni produkt vzporenih vektorjev (a•b), ki torej oklepata kot 0 °, kar enak produktu velikosti obeh vektorjev (saj velja cos(0°) = 1, od koder sledi a•b = ab cos(0°) = a•b ). Skalarni produkt pravokotnih vektorjev pa je 0 (saj velja cos(90°) = 0, od koder sledi a•b = ab cos(90°) = 0 ).

Gibalna količina je definirana kot zmnožek mase in vektorja hitrosti:
p = mv.
Zapišimo še vrtilni količini teles (vektorski produkt med vektorsko razdaljo r in gibalno količino – velja za točkasta telesa:
L = rxp = m(rxv).
Vrtilna količina se ohranja (privzeli bomo, da so motnje ostalih teles majhne) in to bo eden glavnih adutov pri izpeljavi enačbe orbit in pri razlagi Keplerjevih zakonov.


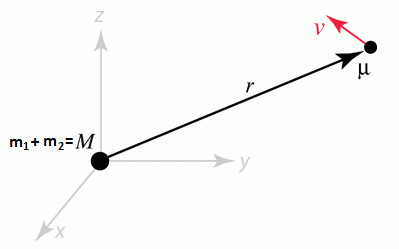
Kot bomo videli, se veliko elegantneje računa, če opišimo sistem kot reducirano maso (μ = m1m2/(m1 + m2)), ki jo privlači centralna sila celotne mase (M = m1 + m2). Velja vektorski zapis: r = r2 –r1 je razdalja med telesoma, v = v2 – v1 je relativna hitrost ter p = μv je gibalna količina. Računi sledijo.


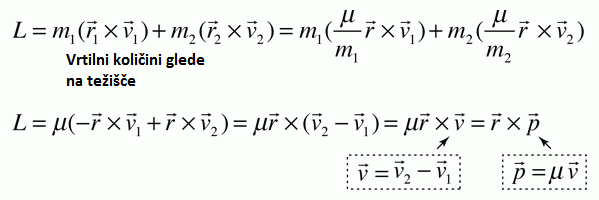
Iz končne enačbe vrtilne količine (L = μrxv) se razbere, zakaj je smiselno opis sistema poenostaviti v reducirano maso (μ = m1m2/(m1 + m2)), ki jo privlači centralna sila celotne mase (M = m1 + m2) na razdalji r.
Še enkrat: p = μv je gibalna količina; v = v2 – v1 je relativna hitrost; razdalja je: r = r2 –r1.
r

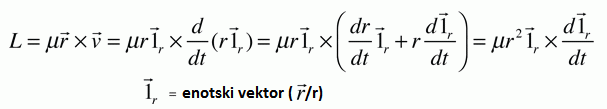
Vektorski produkt enotskega vektorja s samim seboj je 0 ( IrxIr = 0 ), ker je kot 0° (sin(0°) = 0).

Ker ni zunanjih navorov in sil, se sistemu ohranja vrtilna količina. Odvod vrtilne količine je torej po definiciji kar nič.


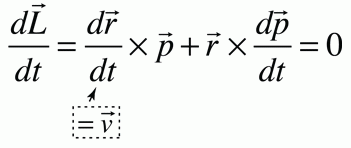
Ta lastnost nam bo prišla še kako prav pri izpeljavi enačbe orbit, še prej pa ponovimo Keplerjeve zakone.

Keplerjevi zakoni


I. Keplerjev zakon
Orbita (pot) planeta je elipsa s Soncem v enem od gorišč.

II. Keplerjev zakon
Zveznica med Soncem in planetom opiše v enakih časovnih intervalih enake ploščine. Ohranja se torej ploščinska hitrost (vrtilna količina).

III. Keplerjev zakon
Kvadrat orbitalne periode planeta je sorazmeren kubu velike polosi elipse.

Nekateri zapišejo III. zakon tudi v obliki razmerij kvadratov časov in kubov polosi:
(T1/T2)2 = (a1/a2)3
Ali v obliki – da je količnik kvadrata siderične periode 'T' in kuba velike polosi elipse 'a' za vse planete enak: T2/a3 = konst.

Pri tretjem zakonu je najbolj korekten prvi zapis (sorazmernost med kvadratom obhoda in kubom velike polosi), druga dva zapisa sta približna, a dokaj dobro veljata, ker je masa planetov 'm' precej manjša od mase Sonca 'M'. V splošnem pri dveh telesih velja, da potujeta okrog skupnega težišča in v tem primeru se danes tretji Keplerjev zakon zapiše v pravilnejši Newtonovi verziji:
T2/a3 = 4π2/(G(M + m))
G je gravitacijska konstanta.
A ker ima večina planetov precej skromne mase 'm' napram masi Sonca M, je poenostavitev T2/a3 ≈ 4π2/(GM) smiselna.

Še beseda o elipsi na preprost način - preko risanja in orbite kometa.

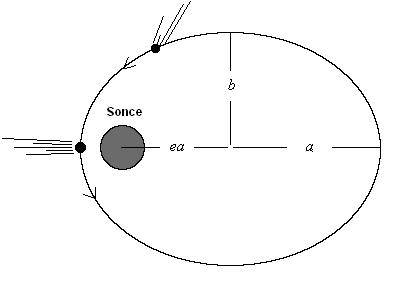
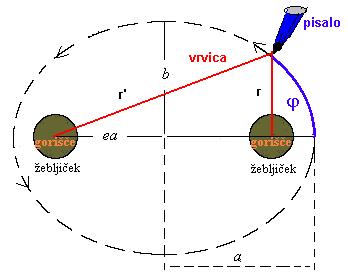
Eliptični tir kometa (levo zgoraj), Sonce je v enem izmed dveh gorišč elipse, a je velika in b mala polos elipse. Ekscentričnost elipse e je definirana kot e = (a2 - b2)1/2/a in zavzema vrednosti med 0 in 1 (0 <= e < 1 ). Slika desno zgoraj prikazuje, kako si za mnoge najlažje predstavimo naravo elipse. Recimo, na ploščo iz plute položimo list, vanj zapičimo dva žebljička, med njima napeljemo vrvico, jo s pisalom napnemo in vlečemo krivuljo, rezultat je elipsa. Žebljička predstavljata gorišči elipse. Iz geometrije na skici velja, da je vsota r' + r konstantna, je enaka dolžini vrvice in vsota izražena z veliko polosjo elipse znaša r'+r=2a. Sedaj nam ne bo težko izračunati razdalje med središčem in goriščem ((a2 - b2)1/2 = e*a). Tudi izpeljava klasičnega, kanoničnega, zapisa enačbe elipse (x2/a2 + y2/b2 = 1) nam ne sme povzročati težav, v astronomiji pa nam največkrat pride prav stožnična oblika v polarnih koordinatah:
r = a(1 - e2)/(1 + e*cos(φ)).

Sledijo dokazi, razlage Keplerjevih zakonov

Drugi Keplerjev zakon


Zveznica med Soncem in planetom opiše v enakih časovnih intervalih enake ploščine. Ohranja se torej ploščinska hitrost (vrtilna količina). Sledi dokaz.


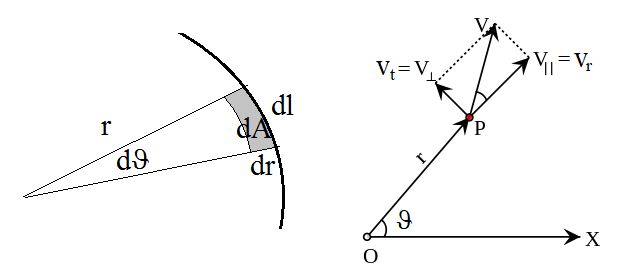
Oznaka za ploščino naj bo A. Pri klasični sliki velja dA/dt = dldr/dt = (rdr)dϑ/dt, po integraciji ( dA/dt = (dϑ/dt)∫rdr = (r2/2)dϑ/dt ) razdalje od 0 do r dobimo rezultat:
dA/dt = (r2/2)dϑ/dt.
vr = dr/dt – radialna hitrost
Vt = rdϑ/dt = rω - je hitrost pravokotna na razdaljo r (glej sliko)
v2 = Vt2 + Vr2
dA/dt = rvt/2
Zapišimo specifično relativno vrtilno količino na maso.
rvt = |rxv| = L/μ

dA/dt = L/(2μ)

Zadnji zapis je dokaz za drugi Keplerjev zakon, saj se vrtilna količina ohranja in s tem tudi ploščinska hitrost.

Zapišimo še nekaj zelo uporabnih relacij, ki izhajajo iz prvega in drugega Keplerjevega zakona.

Za gibanje po elipsi velja:
rp = a(1-e) – razdalja od gorišča do perihelija (prisončja)
ra = a(1+e) – razdalja od gorišča do afelija (odsončja)

Ohranja se vrtilna količina, znamo ju zapisati za perihelij in afelij:
μrpvp = μrava – vrtilni količini v periheliju in afeliju
vp/va = (1+e)/(1-e)

Zapišimo celotno energijo reducirane mase (vsoto kinetične in potencialne energije v točki najbližji težišču, recimo Soncu v periheliju):
E = μvp2/2 - GμM/(a(1-e)) = μva2/2 - GμM/(a(1+e)) = μva2/2 - Gμ(m1 + m2)/(a(1+e))

Uporabimo enačbe o ohranitvi vrtilne količine [ in ne pozabimo, da je M = (m1 + m2) ], od koder sledi:
vp2 = (GM/a)(1+e)/(1-e)
va2 = (GM/a)(1-e)/(1+e)

L = μrpvp – vrtilna količina (vanjo vstavimo rp in vp)
L = μ(GMa(1-e2))1/2 = μ(G(m1 + m2)a(1-e2))1/2

L2 = μ2(G(m1 + m2)a(1-e2))

Po upoštevanju zgornjih povezav dobimo za celotno energijo v periheliju (μvp2/2 - GμM/rp ) izraz »vis-viva«:
E = μvp2/2 - GμM/(a(1-e)) = μ(GM/2a)(1+e)/(1-e) - GμM/(a(1-e))
E = - GμM/(2a) = - Gm1m2/(2a)
Ali - če polos a zamenjamo z a-jem izraženim iz enačbe L = μ(GMa(1-e2))1/2, dobimo:
E = - μ(GMμ/L)2(1 – e2)

Sedaj lahko poiščemo še hitrost v poljubni točki orbite:
μv2/2 - GμM/r = - Gm1m2/(2a)

v2 = G(m1+m2)(2/r – 1/a)

Za r lahko vstavimo enačbo: r=a(1-e2)/(1+e*cos(φ)).
Od tu naprej pa se da lepo animirati gibanje preko rač. programa.

Tretji Keplerjev zakon


Kvadrat orbitalne periode planeta je sorazmeren kubu velike polosi elipse.

Najprej zapišimo ploščinsko hitrost (dA/dt), ki je enaka vrtilni količini deljeni z reducirano maso (L/(2μ)).

dA/dt = L/(2μ)
∫dA = L/(2μ)∫dt - integriramo po celotni površini A in obhodnem času T.
Integral po celotni periodi (T = to je obhodni čas) in ploščini A velja:
A = toL/(2μ) = TL/(2μ)
Ploščina elipse je: A = πab.

Zapišimo kvadrat obhodnega časa:
T2 = A24μ2/L2
T2 = 4π2a2b2μ2/L2
Ker veljata zvezi: L = μ(GMa(1 - e2))1/2 ter b = a(1 - e2)1/2

Sledi končni izraz za izpopolnjeni tretji Keplerjev zakon:

T2 = 4π2ab2/(GM(1-e2)) = 4π2a3/(G(m1+m2))


Še dokaz, da je gibanje zaradi centralne sile sorazmerne z 1/r2, v resnici gibanje po orbiti stožnic, po: krogu, elipsi, paraboli, hiperboli.

Sledi torej dokaz za prvi Keplerjev zakon.


Za uvod si še enkrat oglejmo enačbe eliptičnega tira planeta in drugi Keplerjev zakon. Podatki pomembni za matematični opis elipse so: ε ali e je ekscentričnost elipse (e = ε = (rmaks - rmin)/(rmaks + rmin) ali b = a(1 - e2)1/2), a je velika polos elipse, b je mala polos elipse, Θ je kot med zveznico r, ki povezuje gorišče elipse s točko na elipsi in veliko polosjo elipse, glejte sliko.
Velja: r = a(1 - ε 2 )/(1 + ε cos Θ).


Iščemo torej razdaljo r izraženo brez časa in hitrosti, tako bomo prišli do enačbe orbit. Uporabili bomo zakon o ohranitvi vrtilne količine in Newtonov gravitacijski zakon, iz katerega bomo izrazili pospešek a. Raziskali bomo vektorski produkt med pospeškom in vrtilno količino, ki ga bomo izrazili z odvodom hitrosti in vrtilne količine ter nato poiskali integral, ki s skalarnim produktom r vrne kvadrat vrtilne količine. To je ena krajših, a še zmeraj korektnih poti do končne enačbe orbit. Pomagajte si s priloženo geometrijo vektorskega računa in s skicami orbit. To je v resnici izpeljava orbit preko »Laplace–Runge–Lenzovega« vektorja , ki je sorazmeren vektorju glavne osi elipse (stožnic).


Še enkrat se spomnimo (slika zgoraj), da opisujemo sistem kot reducirano maso (μ = m1m2/(m1 + m2)), ki jo privlači centralna sila celotne mase (M = m1 + m2). Velja: vektorska razdalja je r = r2 – r1, relativna hitrost je v = v2 – v1, gibalna količina je p = μv.

Zapišimo pospešek a (uporabimo gravitacijski zakon, ker enotski vektor kaže od masivnejšega k lažjemu telesu – glejte sliko - uporabimo še negativni predznak pri vektorskem zapisu, kar pomeni, da je sila privlačna), hkrati pa še izvedimo vektorski produkt med pospeškom in vrtilno količino. Kot smo že pokazali, je vrtilna količina kar L = μrxv (končni rezultat pa bo L = μr2lrx(dlr/dt)). Uporabili bomo nekaj klasičnih pravil pri računanju z vektorji:


Vektorski produkt pospeška in vrtilne količine lahko zapišemo tudi kot odvod po času vektorskega produkta hitrosti in vrtilne količine (dokaz: d(vxL)/dt = (dv/dt)xL + 0 = axL = GMμdlr/dt). Hkrati pa je zelo poučen obraten proces, to je rezultat po integraciji produkta vxL = ∫(GMμdlr/dt)dt = GMμlr + D (kot bomo videli je konstanta, vektor D, sorazmerna vektorju velike polosi, recimo elipse, ki pa kot vemo ni odvisen od časa – velika polos namreč ohranja smer in dolžino, zato je njen odvod po času 0, D se tudi imenuje Laplace–Runge–Lenz vektor). Še več pa nam razkrije sam skalarni produkt integrala z razdaljo r (velja r•D = rDcosΘ). Skalarni produkt nam bo odpravil vektorski zapis in razkril enačbo orbit za gibanje teles na katere deluje centralna sila sorazmerna z 1/r2 (če smo pošteni, oče te izjemne enačbe je kar Johannes Kepler).


Slika: D = vxL - GMμlr je Laplace–Runge–Lenz vektor (LRL), ki ohranja smer in velikost glavne osi elipse (apside) - kar pa zaradi relativističnih efektov le delno drži. V večini literature je vektor LRL podan s črko A, povezava z D pa je preko enačbe A = mD = mvxL - GmMμlr = pxL - GmMμlr. Pri našem zapisu vektorja D gre v bistvu za normiranje vektorja A z maso objekta m, ki mu določamo orbito.
Seveda je Laplace–Runge–Lenz vektor pri krožni orbiti kar enak 0 (krožnica nima dominantne smeri, osi), saj velja enakost med vektorjema vxL in GMμlr. Vektorja sta vzporedna in enako dolga, saj je radialna komponenta hitrosti po celotni orbiti enaka 0 in velja kar absolutna enakost GMμ = vL = rμv2, oziroma Fc = GMμ/r2 = μv2/r. To je znana enačba za centripetalno silo pri kroženju, ki jo je izpeljal že Huygens.

Še strnjen izračun za poljubno orbito povezano s silo sorazmerno z 1/r2:





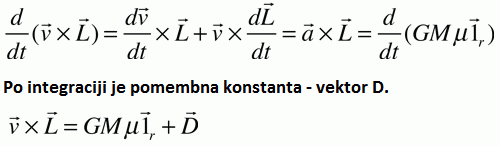
Leva stran enačbe je sorazmerna kvadratu vrtilne količine ( (rxv)•L = L2/μ ), ki se ohranja, deljena z reducirano maso. Če sedaj izrazimo razdaljo r, le ta ne vsebuje več ne časa in ne hitrosti. Tako smo prišli do dokaza, iskane enačbe orbit, ki je tudi formalno matematični zapis stožnic.

Za končni zapis enačbe orbit v polarnih koordinatah uporabimo še spodnje relacije od prej ali dobljene preko primerjav:
e = D/(GMμ)
L = μ(GMa(1-e2))1/2
b = a(1-e2)1/2

Tako smo izpeljali končno enačbo orbit, za elipso velja:

Če je ekscentričnost e = 0, je orbita kar krožnica!

Do tega izjemnega rezultata je genialni Kepler prišel pred približno 400 leti preko originalne obdelave večletnih merjenj poti (lege) Marsa na zvezdnem ozadju in tako odprl pot nebesni mehaniki, posredno tudi teoriji relativnosti. Obdelal je tri Marsove cikle po 687 dni (tudi preko Brahejevih meritev, ki pa jih Brahe žal ni znal matematično obdelati). V bistvu je Kepler iskal paralakso Marsa po vsakem njegovem obhodu okrog Sonca na zvezdnem ozadju gledano iz Zemlje in tako geometrijsko določil orbito Zemlje, ki je eliptična (popravek intuitivno napačno določene orbite Zemlje kot krožnice, je torej elipsa – J. Kepler je eden največjih umov vseh časov). Kepler ni poznal nobene razdalje, ne razdalje Mars-Zemlja in ne Zemlja-Sonce (ta je bila sicer zelo grobo ocenjena …), a vendar je izpeljal točna razmerja med parametri elips, razdaljami in obhodnimi časi ter relativnimi hitrostmi. Poznal je samo obhodne čase bližnjih planetov glede na zvezde in relativne lege Marsa med zvezdami v časovnem zaporedju – a podrobneje o tem kdaj drugič.



Še beseda o Laplace–Runge–Lenz vektorju D ali A. Le ta se v resnici pri planetih rahlo vrti zaradi navora ostalih planetov in delno Sonca, del rotacije pa je posledica mehanizmov, ki jih pravilno opiše le splošna relativnost (v resnici se ves čas spreminja energija planeta, hitrost in razdalja do Sonca – gibanje po elipsi - in s tem se spreminja masa po zvezi E/c2, kar povzroči dodatno precesijo). Zagotovo velja, če je D = vxL - GMμlr in če D odvajamo po času, nam po odvajanju zagotovo ostane člen dD/dt = -Glrd(Mμ)/dt (masi m1 in m2 se rahlo spreminjata zaradi neenakomerno pospešenega gibanja po elipsi – glejte sliko). To je sicer premislek iz posebne teorije relativnosti, ko privzamemo zgolj spremembo mase zaradi spremembe energije (E/c2), a konceptualno gre razmišljanje v pravo smer. Dodatni potencial, ki povzroča precesijo je kar sorazmeren z -1/r3, sila pa se izrazi kot:





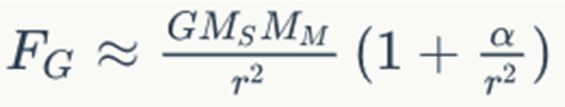
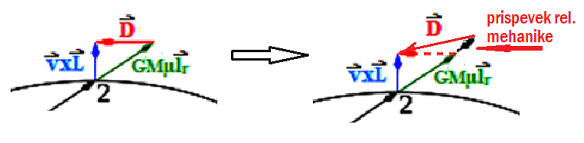
- izpeljano na strani - Zakaj astronomija - in zakaj tudi v šoli? (XIII) .

Izpeljava orbit preko Laplace–Runge–Lenzovega vektorja in dopolnitev le tega z vplivom relativistične mehanike, je ena najbolj nazornih poti tako do enačb orbit, kot do razlage – zakaj orbite planetov rahlo precesirajo (saj LRL vektor D v resnici, zaradi spreminjajoče se relativistične mase, ne ohranja smeri, pokazali z odvodom). Izpeljava precesije je zgolj fenomenološka – in ni čisto korektna, ker nismo upoštevali vseh postulatov splošne teorije relativnosti – recimo, da sprememba gravitacije potuje s končno hitrostjo (svetlobe), da je čas odvisen od pospeška, gravitacije. Splošna teorija relativnosti pa tudi ne uporablja več globalne gravitacijske sile, ampak koncept ukrivljenosti prostor-časa, ukrivlja ga masa zvezd, galaksij in ostale oblike energij. Korektna razlaga in izpeljava sledita naslednjič.


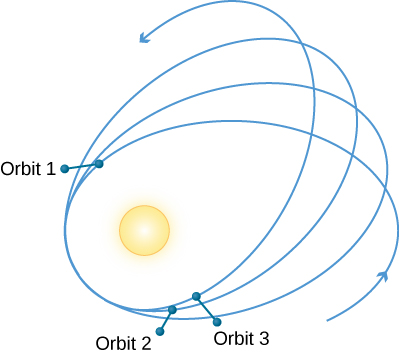
Precesija Merkurjevega perihelija, oziroma glavne osi elipse, zaradi relativističnih efektov (izpeljano na strani - Zakaj astronomija - in zakaj tudi v šoli? (XIII) ). Gibanje planetov torej ni čisto eliptično, ampak po krivulji rozete – narava nas torej zmeraj znova preseneča!


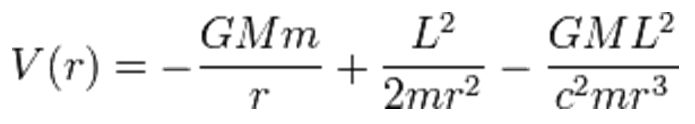
Pravilen potencial V(r) dvojnega gravitacijskega sistema sferičnih teles da (kdo drug kot) elegantna Schwarzschildova metrika, še enkrat glejte že omenjeno stran: Zakaj astronomija - in zakaj tudi v šoli? (XIII).



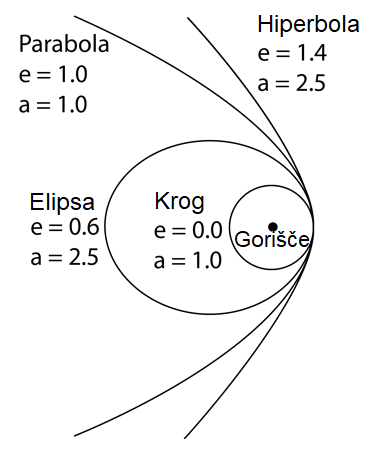
Zapišimo enačbo orbit v polarnih koordinatah – najprej za elipso:


Upoštevajmo še »vis-viva« enačbo za energijo in naredimo analizo gibanj glede na energijo, recimo nekega nebesnega telesa (kometa, sonde):
E = - μ(G(m1 + m2)μ/L)2(1 – e2)

* - če je ekscentričnost 0 ≤ e < 1, je orbita elipsa (vsota kinetične in potencialne energije je negativna):
Ek + Ep < 0 ali Ek < -Ep,

* če e = 0 je orbita krožnica (spet je seveda vsota kinetične in potencialne energije negativna):
Ek + Ep < 0 ali Ek < -Ep,

* - če je ekscentričnost e = 1, je orbita parabola (absolutna kinetična in potencialna energija sta enaki in njuna vsota je 0 ):
Ek + Ep = 0 ali Ek = -Ep,

* - če e > 1, je orbita hiperbola (skupna energija je pozitivna -(1 – e2) > 0 ):
Ek + Ep = -μ(GMμ/L)2(1 – e2) > 0 ali Ek > -Ep.


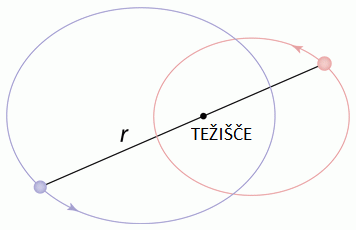
V dvojnem vezanem sistemu (dvozvezdje), je orbita elipsa za vsako zvezdo posebej in težišče obeh teles je v gorišču obeh orbit, elips.

Primeri uporabe nebesne mehanike


Podajmo še primer za sondo Voyager 1 (lansirana 5. septembra 1977, je trenutno od nas najbolj oddaljen objekt, ki je delo človeških rok). Na razdalji r = 17 milijard km od Sonca je sonda imela hitrost v = 17,1 km/s in, kot bomo videli, potuje po hiperboli:

E = μv2/2 - GμM/r = Gm1m2/(2a)

Reducirana masa je v tem primeru (ko je mv/mS ≈ 0) kar masa sonde Voyager 1:
μ = mvmS/(mS(1 + mv/mS)) = mv/(1 + mv/mS) ≈ mv.
Skupna masa pa je kar masa Sonca: M = mS.

M☉ = mS = 1,99*1030 kg, G = 6,67408×10-11 m3·kg-1·s-2
Tako se naša »vis-viva« enačba (po krajšanju mase Voyagerja) glasi:
v2/2 - GmS/r = GmS/(2a) = 138 km2s-2.

V neskončnosti v∞, kjer velja 1/r = 0 pa bo hitrost enaka (v∞2/2 + 0 = 138 km2s-2):
v∞ = 16.6 km/s


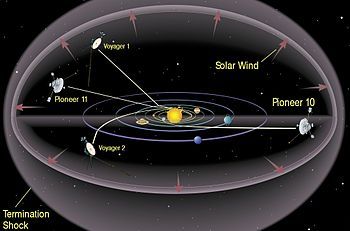
A to bo še zmeraj premajhna hitrost, da bi Voyager 1 zapustil gravitacijo Rimske ceste, tukaj so še vplivna območja drugih teles.

Ocenjena hitrost Sončevega sistema okrog jedra Rimske ceste je približno 230 km/s, galaktična ubežna hitrost pa znaša približno 550 km/s (ocene so od 492 do 594 km/s). Torej, v smeri vektorja hitrosti Sončevega sistema je relativna ubežna hitrost iz naše Galaksije približno 550 km/s - 230 km/s = 320 km/s, a še prej je potrebno pobegniti iz Zemlje in Sončevega privlaka. Zadnje ocene mase naše Galaksije so od 0.8 – 1.5×1012 M☉, znotraj orbite Sonca pa znaša masa Galaksije okrog 7×1010 M☉. Število zvezd je ocenjeno na 100–300 milijard. Oddaljenost Sonca od središča Galaksije bi naj bila od 24000 do 28400 svetlobnih let. Okrog središča galaksije pa bi naj potovali 225 do 250 milijonov let. Če starost Zemlje (4,5 milijarde let) delimo z obhodnim časom okrog središča Galaksije (tako določimo število obhodov), nam rezultat pove, da smo doslej naredili zgolj 19 galaktičnih let (smo ravno polnoletni). Torej smo galaktično še zelo mladi.

Ubežno hitrost iz neke razdalje r od objekta z maso M izračunamo iz zakona o ohranitvi energije (E = Ek + Ep = Ek∞ + Ep∞) . Ubežna hitrost pomeni, da bo telo v neskončnosti imelo hitrost 0 (kjer velja 1/r∞ = 0 in v∞ = 0).
Ek + Ep = Ek∞ + Ep∞
mv2/2 - GmM/r = mv2∞/2 - GmM/r∞
V2/2 - GM/r = 0 – 0
V = (2GM/r)1/2 – je ubežna hitrost iz razdalje r od sferičnega telesa z maso M

Za vajo izračunajte ubežno hitrost z Zemlje (polmer Zemlje je 6371 km, masa Zemlje je 5.97237×1024 kg) – ta hitrost znaša vIIZ = (2GMz/rz)1/2 = 11,2 km/s.
Izračunajte še ubežno hitrost glede na Sonce iz orbite Zemlje (razdalja je ae = 150 milijonov km) – ta hitrost pa znaša 42,1 km/s.

Vprašajmo se še, s kakšno hitrostjo vx moramo izstreliti raketo glede na Zemljo, da bo le ta v neskončnosti ušla gravitaciji Zemlje in Sonca.

Ker Zemlja potuje okrog Sonca s povprečno hitrostjo 29,8 km/s (izračunajte to vrednost), izstrelimo raketo v smeri gibanja Zemlje, tako da rabimo daleč vstran od Zemlje samo še dodatno hitrost vrel = 42,1 km/s - 29,8 km/s = 12,3 km/s. A še prej moramo ubežati privlaku Zemlje, ta je (vIIZ = (2GMz/rz)1/2 = 11,2 km/s ali V2IIZ/2 = GMz/rz).
Vprašajmo se torej, s kakšno hitrostjo vx moramo izstreliti raketo glede na Zemljo, v smeri gibanja Zemlje, da bo le ta imela hitrost vrel =12,3 km/s zelo daleč vstran od površine (1/r∞ = 0). Uporabimo zakon o ohranitvi energije v neskončnosti glede na Zemljo in na površini Zemlje.
mV2x/2 - GmMz/rz = mV2rel/2 - GmMz/r∞
V2x/2 - GMz/rz = V2rel/2 – 0
V2x/2 - V2IIZ/2 = V2rel/2
V2x - V2IIZ = V2rel
Končni rezultat hitrosti vx izstrelitve rakete glede na Zemljo, da bo le ta v neskončnosti ušla gravitaciji Zemlje in Sonca, je kar forma Pitagorovega izreka:
Vx = (V2rel + V2IIZ)1/2 = ((12,3 km/s)2 + (11,2 km/s)2)1/2 = 16,6 km/s

Če upoštevamo še izstrelitev v smeri rotacije Zemlje na Ekvatorju, so te hitrosti še nekoliko manjše. A sondi Voyager sta imeli na začetku nekoliko manjše hitrosti, saj sta obiskovale planete, ki so jima spet povečevali hitrosti, a sta po opravljenih slikanjih in meritvah spet ušli gravitaciji samega planeta in se usmerile do naslednjega (to je sistem gravitacijske frače – glej sliko).


Graf prikazuje hitrosti sonde Voyager 2, ki je na poti v svojo korist uporabila gravitacijske privlake ostalih planetov– princip vesoljske frače. Zato je tudi začetna hitrost (okrog 36 km/s) bila manjša od ubežne (42,1 km/s) glede na Sonce.
Naš rojak Anton Mavretič je v okviru projektov Voyager 1 in Voyager 2 sodeloval pri izdelavi plazemskega spektrometra PLS – Plasma Spectrometer - izjemno uspešno je vodil skupino inženirjev, instrument še deluje.


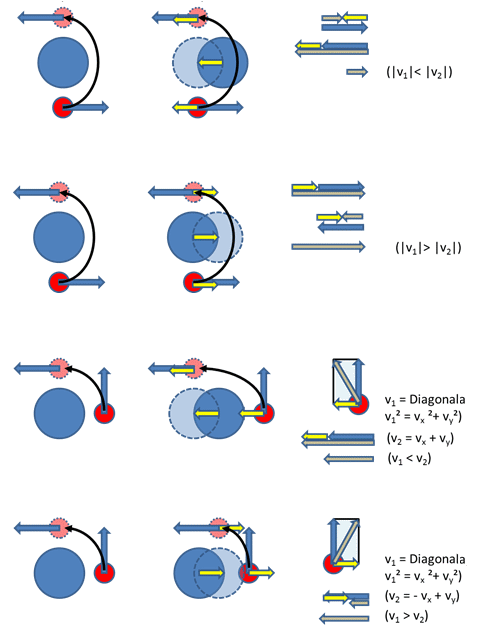
Vesoljska (gravitacijska) frača, princip delovanja – planet ujame sondo in jo preusmeri, nekaj primerov. Levo je pogled iz planeta, na sredi iz Sonca (rumene puščice kažejo hitrost planeta glede na Sonce), desno pa izračun vektorskih hitrosti sond (sive puščice predstavljajo začetne v1 in končne v2 hitrosti sond glede na Sonce). Rdeč poln krogec je začetek, črtkan svetlejši krogeč pa konec dogodka za izračun. Hitrosti se kdaj povečajo (to velikokrat uporabijo pri sondah, ki raziskujejo Sončev sistem – sonde letajo od planeta do planeta, do lun), kdaj pa zmanjšajo. Zmeraj pa je hitrost sonde, glede na planet, ubežna (to je gibanje po hiperboli ali blizu te krivulje – zakaj blizu - ker na sonde deluje več sil, planet-i, Sonce), razen če sonda želi krožiti ali celo pristati na kakem izmed planetov (večkrat smo že s sondami, seveda brez posadke, pristali na Marsu, tudi Veneri, se spustili v plinska velikana Jupiter, Saturn …).
Logika je prav enaka kot v prejšnjem primeru, ko smo računali s kakšno hitrostjo vx moramo izstreliti raketo glede na Zemljo, da bo le ta v neskončnosti ušla gravitaciji Zemlje in Sonca. Zemlja s svojo orbitalno hitrostjo okrog Sonca in lastno gravitacijo, že predstavlja tako gravitacijsko fračo.
Neke vrste gravitacijsko fračo so odkrili tudi, ko sta se dve galaksiji in seveda črni luknji gravitacijsko ujeli in sta naknadno ujeli še tretjo črno luknjo (velikosti 20 milijonov Sončevih mas), ki pa je odfrčala iz sistema in za sabo potegnila dolgo sled zvezd ... – zanimivo (posnel še zmeraj izjemen teleskop Hubble).

Pri projektu Voyager je imel veliko vlogo tudi naš rojak dr. Anton Mavretič (NASA). Vodil je ekipo, ki je izdelala senzor Sončevega vetra, kateri je določil, kdaj je sonda dosegla rob vpliva Sonca (rob heliosfere - ko tok Sončevega vetra postane manjši od toka medzvezdnih delcev). Dr. Anton je izjemen strokovnjak, seveda tudi celotna ekipa, saj je naredila sondo in inštrument, ki deluje desetletja v hladu vesoljske praznine.

Sondi Voyager 1 in 2 sta s seboj ponesli tudi podatke o človeški civilizaciji. Ti so shranjeni na pozlačeni bakreni gramofonski plošči (LP – zanimivo, kako zelo se je tehnologija zvočnega zapisa spremenila v pretečenem času – a narava zvoka ostaja večna), spravljeni v aluminijasto skrinjo, na kateri so vgravirana navodila za uporabo, priložena pa je še gramofonska igla. Plošča, ki nosi naslov Zvoki Zemlje (The Sounds Of Earth), vsebuje štiri tematske skupine podatkov, med katerimi so zvoki narave in živali, človeški govor (pozdravi v različnih jezikih) glasba (ljudske in umetne skladbe: Mozart, Blind Willie Johnson, Chuck Berry in Valya Balkanska) in tudi slike.
V tem kontekstu ni odveč mlade opozoriti na šalo, ki kroži po spletu, da so se Nezemljani na Voyagerjev zvočni zapis odzvali le s štirimi besedami "pošljite več Chucka Berrya" ("Send more Chuck Berry"), Chuck Berry je eden od očetov rock & rolla, ki je v svojem res, za glasbenika, dolgem življenju (91 let) igral, nastopal, zabaval občinstvo praktično do konca, oziroma začetka poti v večnost 2017 (ko je že pozabljal besedila, kitarske akorde, rife).
Seveda, astronomija prežema vso našo kulturo in tudi kultura prežema astronomijo, sploh v Sloveniji se v tej smeri trudi kar nekaj umetnikov.


Tako nam je nebesna mehanika omogočila raziskovanje globin vesolja in novo upanje pri komunikaciji z morebitnim življenjem v medzvezdnih prostranstvih.

Več v ostalih poglavjih.

Povzel (maj 2018): Vičar Zorko