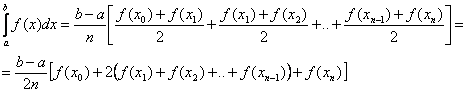Metoda trapezov

Pri tej metodi namesto ploščin pravokotnikov na posameznih podintervalih vzamemo ploščine

trapezov, ki nastanejo, če loke krivulje f(x) v vsakem podintervalu nadomestimo z ustreznimi

tetivami krivulje.


Približno vrednost integrala lahko izrazimo z vsoto:




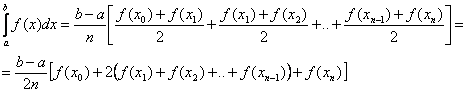
Ta metoda daje boljše približke od metode pravokotnikov, seveda je tudi pri tej metodi stopnja

natančnosti odvisna od števila podintervalov n.

FUNCTION F(X)
F=x*x*log(x)
RETURN
END
 
WRITE(*,*)' Podaj meji:'
READ (*, *) A, B
WRITE(*,*)' Podaj stevilo delitvenih tock:'
READ (*, *) N
H=(B-A)/(N-1)
TI=F(A)+F(B)
DO X=A+H,B-0.9*H,H
TI=TI+2*F(X)
ENDDO
TI=TI*H/2
WRITE(*,*)' INTEGRAL=',TI
END