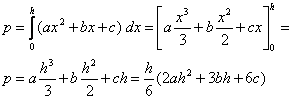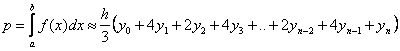Simpsonova metoda


Naj bodo v ravnini dane tri točke tako, da je abscisa srednje točke enaka

aritmetični sredini abscis ostalih dveh točk. Njihove koordinate naj bodo:


T₁(0,y₁)

T₂(h/2,y₂)

T₃(h,y₃)


Skozi tri točke poteka enolično določena parabola druge stopnje, ki jo zapišemo z enačbo y=ax²+bx+c.


V enačbo y=ax²+bx+c vstavimo koordinate točk T₁, T₂ in T₃ter dobimo parametre a,b in c.
Parametri a,b in c so določeni z naslednjim sistemom enačb:


Y₁=c

Y₂=ah²/4+bh/2+c

Y₃=ah²+bh+c


Ploščina lika, ki ga oklepa parabola z abscisno osjo med ordinatama v točkah x=0 in x=h

je dana z določenim integralom:





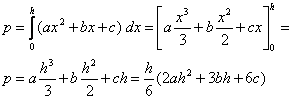
Če sedaj enačbo Y₂=ah²/4+bh/2+c pomnožimo s 4 dobimo:


4Y₂=ah²+2bh+4c


in seštejemo Y₁+4Y₂+Y₃=c+ah²+2bh+4c+ah²+bh+c=2ah²+3bh+6c.

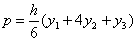
Ploščino omenjenega lika izračunamo torej naravnost iz koordinat danih točk, ne da bi morali

najprej določiti parametre ustrezne parabole druge stopnje.

V tistih točkah na abscisni osi, ki imajo sode indekse, imamo postavljene ordinate.

Lik med krivuljo f(x) in abscisno osjo ter ordinatama v točkah a in b razdelimo na n pasov širine
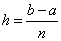, kjer je vedno po ena točka z lihim indeksom ravno razpolovišče ustreznega podintervala.



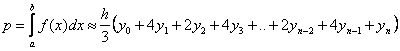
Zgornjo enačbo za izračun približne vrednosti določenega integrala imenujemo Simpsonovo formulo.

Ta metoda, da boljše približke kot metoda pravokotnikov ali trapezna metoda.Število delitvenih

točk pri simpsonovi metodi mora biti liho. Približek računanja je tem boljši čim večji je n.


FUNCTION F(X)
F=X*X*ALOG(X)
RETURN
END

WRITE(*,*)'Podaj meji:'
READ(*,*)A,B
WRITE(*,*)'Podaj stevilo delitvenih tock:'
READ (*,*)N
IF(MOD(N,2).EQ.0) STOP 'Stev. del. tock mora biti liho'
SI=F(A)+F(B)
H=(B-A)/(N-1)

DO X=A+H,B-0.9*H,2*H
SI=SI+4*F(X)
ENDDO

DO X=A+2*H,B-1.9*H,2*H
SI=SI+2*F(X)
ENDDO

SI=SI*H/3
WRITE(*,*)'INTEGRAL=',SI
END