SEKANTNA METODA
Kadar je računanje odvoda funkcije dolgotrajno, uporabimo sekantno metodo.
Za določitev ničle nelinearne funkcije f(x) najprej izberemo dva približka x0 in x1.
Nadomestimo nelinearno funkcijo s sekanto skozi točki (x0,f(x0))
in (x1,f(x1)) ter izračunamo kje sekanta seka os x. To
presečišče je novi približek x2. Nato postavimo novo sekanto skozi
točki (x1,f(x1)) in (x2,f(x2)) in
nadaljujemo postopek.
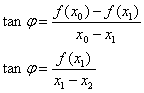
zgornji enčbi izenačimo in dobimo:
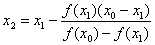
Nadaljne približke izračunamo po formuli:
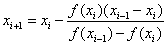
Algoritem sekantne metode:
1.postavimo indeks i=0,izberemo začetna približka x0,x1 izberemo dopustno
relativno napako ε, določimo maksimalno število iteracij (ponovitev).
2.izračunamo nov približek xi+1 po formuli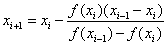
3.če je izvedemo predpisano maksimalno število iteracij se program ustavi, računanje prekinemo. Pomeni, da
xi+1 ni primeren približek rešitve enačbe.
4.če je 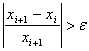 , povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi+1,dober približek
rešitve enačbe α. Ponavljanje zaključimo.
, povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi+1,dober približek
rešitve enačbe α. Ponavljanje zaključimo.
FUNCTION F(X)
F=X-EXP(-X)+0.3*SIN(X)
RETURN
END
WRITE(*,*)'Podaj zacetna priblizka:'
READ(*,*)X0,X1
WRITE(*,*)'Podaj zahtevano natancnost:'
READ(*,*)ES
WRITE(*,*)'Podaj maksimalno stevilo iteracij:'
READ(*,*)MAXIT
ITER=0
EP=1.1*ES
DO WHILE(EP.GT.ES.AND.ITER.LT.MAXIT)
WRITE(*,10)ITER,X0
ITER=ITER+1
X2=X1-F(X1)*(X0-X1)/(F(X0)-F(X1))
IF(X1.NE.0.0)THEN
EP=ABS((X1-X0)/X1)
ENDIF
X0=X1
X1=X2
ENDDO
WRITE(*,*)'Koren=',X0
WRITE(*,*)' Dosezena natancnost=',EP
WRITE(*,*)' Stevilo iteracij=',ITER
10 FORMAT(I5,F14.6)
END

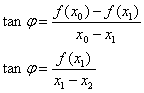
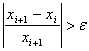 , povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi+1,dober približek
rešitve enačbe α. Ponavljanje zaključimo.
, povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi+1,dober približek
rešitve enačbe α. Ponavljanje zaključimo.