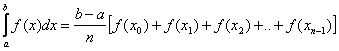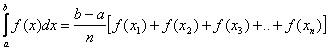Pravokotniška metoda


Interval [a,b] razdelimo na n enakih delov. Širina vsakega podintervala je (b-a)/n.

Vrednost določenega integrala lahko aproksimiramo z vsoto ploščin pravokotnikov, ki imajo širino

(b-a)/n, višina pa je vsakokrat funkcijska vrednost v začetni ali končni točki podintervala.

Tako dobimo formulo:

Ploščine pravokotnikov v začetnih točkah podintervalov:



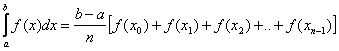
ali

Ploščine pravokotnikov v končnih točkah podintervalov:



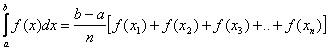
V obeh primerih je seveda približek tem boljši, čim večje je število podintervalov n.

FUNCTION F(X)
F=x*x*log(x)
RETURN
END

WRITE(*,*)'Podaj meji:'
READ (*, *) A,B
WRITE(*,*)'Podaj stevilo delitvenih tock:'
READ (*, *) N
H=(B-A)/(N-1)
RI=F(A)+F(B)

DO X=A+H,B-0.9*H,H
RI=RI+F(X)
ENDDO
RI=RI*H
WRITE(*,*)'INTEGRAL=',RI
END