NAVADNA ITERACIJSKA METODA
Pri navadni iteracijski metodi nelinearno enačbo f(x)=0 prevedemo v ekvivalentno obliko:
x=g(x)
Poiskati moramo tako vrednost α, da je α =g(α) in je f(α)=0.
Enačba x=g(x) pove,da je rešitev enačbe f(x)=0 tista vrednost x=α, pri kateri se funkciji y=x
in y=g(x) sekata.
Algoritem navadne iteracijske metode:
1.postavimo indeks i=0,izberemo začetni približek x0,
izberemo dopustno relativno napakoε, določimo maksimalno število iteracij (ponovitev).
2.izračunamo nov približek xi+1 po formuli xi+1=g(xi).
3.če je izvedemo določeno maksimalno število iteracij se program ustavi, računanje prekinemo. Pomeni, da
xi+1 ni primeren približek rešitve enačbe.
4.če je 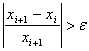 , povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi+1,dober približek rešitve enačbe α. Ponavljanje zaključimo.
, povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi+1,dober približek rešitve enačbe α. Ponavljanje zaključimo.

Graf prikazujefunkciji y=exp(-x) in y=x+0.3*sin(x). Presečišče je približno pri 0.48 .
Zaporedje približkov x1,x2,x3 konverigira(se
približuje) h korenu enačbe f(x)=0, če je blizu korena 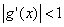 .
.
! resujemo enacbo x=exp(-x)-0.3*sin(x)
G(X)=EXP(-X)-0.3*SIN(X)
WRITE(*,*)'Podaj zacetni priblizek:'
READ*,X0
WRITE(*,*)'Podaj zahtevano natancnost:'
READ*,ES
WRITE(*,*)'Podaj maximalno stevilo iteracij:'
READ*,MAXIT
ITER=0
EP=1.1*ES
DO WHILE(EP.GT.ES.AND.ITER.LT.MAXIT)
WRITE(*,10)ITER,X0
ITER=ITER+1
X1=G(X0)
IF(X1.NE.0.0)THEN
EP=ABS((X1-X0)/X1)
ENDIF
X0=X1
ENDDO
WRITE(*,*)'Koren=',X0
WRITE(*,*)'Dosezena natancnost=',EP
WRITE(*,*)' Stevilo iteracij=',ITER
10 FORMAT(I5,F14.6)
END

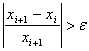 , povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi+1,dober približek rešitve enačbe α. Ponavljanje zaključimo.
, povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi+1,dober približek rešitve enačbe α. Ponavljanje zaključimo.