BISEKCIJSKA METODA
Pri bisekcijski metodi moramo najprej poiskati takšen interval (xl,xd),
da funkcija f(x) na tem intervalu natanko enkrat zamenja predznak.
Če velja f(xl)*f(xd)<0,je koren zaprt v interval xl < α < xd.
Pri bisekcijski metodi interval, ki vsebuje koren, na vsakem koraku iteracije razpolovimo.
Pri nadaljnem računanju obdržimo tisto polovico intervala, v kateri ima funkcija na krajiščih
nasprotni predznak. Z zmanjševanjem intervala se z mejama poljubno približamo korenu enačbe.
Algoritem bisekcijske metode
1.postavimo indeks i=1,izberemo začetni meji xl in xd intervala, da velja
f(xl)*f(xd)<0,
določimo dopustno relativno napako ε, določimo maksimalno število iteracij (ponovitev).
2.izračunamo razpolovišče 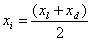 in funkcijski
vrednosti f(xl) in f(xi). Če je f(xi)=0, je xi
koren α in zaključimo ponavljanje.
in funkcijski
vrednosti f(xl) in f(xi). Če je f(xi)=0, je xi
koren α in zaključimo ponavljanje.
3.če imata funkcijski vrednosti f(xl) in f(xi) nasproten predznak je
f(xl)*f(xi)<0 se koren (ničla) nahaja znotraj intervala (xl,xi) in
postavimo xd=xi.
V nasprotnem primeru se koren nahaja znotraj intervala (xi,xd)
zato postavimo xl=xi. Če je i=1 povečamo indeks (števec) in se vrnemo na drugi korak.
4.če je izvedemo predpisano maksimalno število iteracij se program ustavi, računanje prekinemo. Pomeni, da
xi ni primeren približek rešitve enačbe.
5.če je 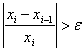 , povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi,dober približek rešitve enačbe α. Ponavljanje zaključimo.
, povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi,dober približek rešitve enačbe α. Ponavljanje zaključimo.
Ker je 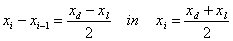 sledi, da je
ocena relativne napake korena
sledi, da je
ocena relativne napake korena 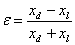 .
.
FUNCTION f(x)
F=X-EXP(-X)+0.3*SIN(X)
RETURN
END
PRINT*,'podaj levo in desno mejo ter stevilo ponovitev:'
READ*,xl,xd,maxit
IF(f(xl)*f(xd)<0) THEN
DO i=1,maxit
x=(xl+xd)/2
IF(f(xl)*f(x)<0) xd=x
IF(f(xl)*f(x)>0) xl=x
IF(f(xl)*f(x)==0) GOTO 10
PRINT*,'x novi=',x,'korak=',i
IF(ABS((xd-xl)/(xd+xl)).LT.0.0005) STOP
ENDDO
ELSE
STOP'pogoj za bisekcijo ni izpolnjen'
ENDIF
STOP
10 PRINT*,'nicla funkcije=',x
END

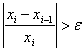 , povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi,dober približek rešitve enačbe α. Ponavljanje zaključimo.
, povečamo indeks i in se
vrnemo na drugi korak. Sicer pomeni, da je xi,dober približek rešitve enačbe α. Ponavljanje zaključimo.