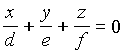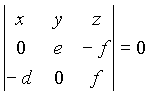
Naj bodo točke D, E in F po vrsti dotikališča stranic trikotnika
a, b in c ter trikotniku včrtane krožnice. Premici BC ter FE naj se sekata v točki D', premici AC in FD v točki E' ter premici AB in ED v točki F'. Po Desarguesovem izreku ležijo točke D', E' in F' na isti premici. Točke D', E' in F' imenujemo Nobby-jeve točke, premico skoznje pa Gergonnejeva premica.Trilinearne koordinate točke D' so: D' = 0 : e : -f, saj sta trojici točk C, B, D' in E, F, D' kolinearni, kar preprosto preverimo (pogoj
za kolinearnost treh točk). Tako so trilinearne koordinate Nobby-jevih točk:D' = 0 : e : -f
E' = -d : 0 : e
F' = d : -e : 0
Enačba Gergonnejeve premice je torej:
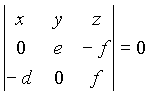
oziroma