PARABOLA rešitve
-
Vstavimo koordinati točke v enačbo in izračunamo
p: y2=8x
-
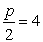 ,
torej je enačba y2=16x
,
torej je enačba y2=16x
-
Preoblikujemo enačbo
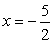 ,
p=5, y2=10x,
,
p=5, y2=10x, 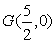
-
Kar je parameter parabole ravno razdalja od gorišča
parabole (ali katerekoli stožnice), do točke, ki je na krivulji ravno "nad
goriščem" (normala na os skozi gorišče), je ena od dveh točk oddaljena
od gorišča za p=5, torej je razdalja med točkama enaka 10. ( Seveda pa
lahko tudi poiščemo ordinato točk na
paraboli, ki imajo absciso isto kot gorišče torej x=5/2.
-
G(2,0) Če vstavimo absciso v enačbo parabole,
dobimo y=6. Točka ime torej koordinate A(9/2,6), gorišče pa G(2,0). Iskana
premica ima enačbo 12x–5y–24=0
-
Premica z naklonskim kotom 1350 ima smerni koeficient
k=–1. koordinati gorišča sta G(–1,0). Tako dobimo premico y=–x–1. Ta seka
parabolo v točkah
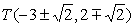 .
Razdalja med njima je 8 enot.
.
Razdalja med njima je 8 enot.
-
Trikotnik je simetričen gleden a x– os, torej
mora njegova stranica oklepati z osjo kot 300. Smerni
koeficient njene nosilke je
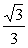 ,
enačba nosilke pa
,
enačba nosilke pa 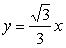 . Ta seka
parabolo v točki
. Ta seka
parabolo v točki 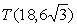 . Ekvivalentno
velja za padajočo nosilko stranice. Razdalja med točkama, ki je enaka stranici
trikotnika pa je potem
. Ekvivalentno
velja za padajočo nosilko stranice. Razdalja med točkama, ki je enaka stranici
trikotnika pa je potem 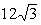 .
.
-
Točki, ki sta za 4,5 oddaljeni od gorišča
s koordinatama G(1,5, 0), sta enako oddaljeni tudi od vodnice z enačbo
x=––1,5. Torej ležita na premici z enačbo x=3. Njuna ordinata pa je
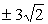 .
.
-
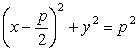
-
Krivulji se sečeta v T(0,09 in A(–3,3). V
točki T mora imeti parabola teme (da bo simetrična glede na abscisno os),
koordinate točke A pa vstavimo v enačbo y2=2px
in dobimo enačbo parabole y2=–3x.
-
Smerni koeficinet nosilke dobimo s formulo
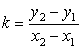 .
Vanjo lahko vstavimo
.
Vanjo lahko vstavimo 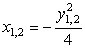 ,
kar dobimo iz enačbe parabole. Če odpravimo dvojne ulomke iz izraz uredimo,
dobimo
,
kar dobimo iz enačbe parabole. Če odpravimo dvojne ulomke iz izraz uredimo,
dobimo 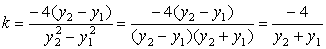 . Ker je točka M
razpolovišče tetive, velja
. Ker je točka M
razpolovišče tetive, velja 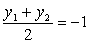 .
Iz tega izračuanmo smerni koeficient 2 in enačbo y=2x+3.
.
Iz tega izračuanmo smerni koeficient 2 in enačbo y=2x+3.
-
Šop premic skozi točko S ima enačbo y+2=k(x+2).
Rešujemo sistem te enačbe in enačbe parabole in pridemo do kvadratne enačbe
ky2–16y+32k–32=0. Da bo
premica tangenta, mora imeti ta enačba dvojno rešitev in torej diskriminanto
enako 0. D=384–256k2. Torej
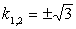 . Enačbi tangent sta
. Enačbi tangent sta 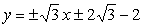 ,
kot med njima pa je 40054'.
,
kot med njima pa je 40054'.
-
Presečišči
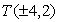 ,
razdalja med njima 8 enot.
,
razdalja med njima 8 enot.
-
-
Enačbo preuredimo v obliko (y–3)2=4(x–2);
torej je p=2, teme T(2,3), gorišče G(3,3)
in vodnica x=1.
-
(y–2)2=–9(x–2); ker je p=–9/2 negativen,
je parabola odprta v levo, torej ima T(2,2), gorišče je levo od temena
G(–1/4,2), vodnica pa desno x=17/4.
-
(x–1)2=8(y–1); p=4; parabola iam
navpično os simetrije torej T(1,1), G(1,3), y=–1(vodnica je vodoravna)
-
(x–6)2=8(y–2); p=4; T(6,2), G(6,4), y=0
-
(y–2)2=4(x–2); p=2; T(2,2), G(3,2), x=1
-
(x–1)2=–4(y+1); p=–2; T(1,–1), G(1,–2), y=0
-
Parabolo lahko zapišemo tudi v obliki (y–2)2=4(x–1)
-
Pri zrcaljenju preko simetrale lihih kvadrantov,
se medsebojno zamenjata x in y in torej dobimo enačbo x2–4x–4y+8=0
oziroma (x–2)2=4(y–1)
-
Če prezrcalimo preko abscisne osi, preide
vsak y v nasprotno število: y2–4x+4y+8=0 oz. (y+2)2=4(x–1)
-
Pri tem zrcaljenju se pretvorijo x v nasprotna števila: y2+4x–4y+8=0
oz. (y–2)2=–4(x+1)
-
(nariši skico) Teme parabole preide v T(–2,1),
parameter ostane p=+2; enačba je (x+2)2=4(y–1) oz. x2+4x–4y+8=0
-
Teme preide v T(–1,–2), p=–2; (y+2)2=–4(x+1) oz. y2+4x+4y+8=0.
NAZAJ K NALOGAM PARABOLA
NAZAJ NA ZAČETEK STOŽNIC
NAZAJ NA DOMAČO STRAN
O.J. april 2001
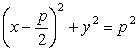
![]()