VPRASANJA ZA POKLICNO MATURO

VPRAŠANJA ZA USTNI DEL

POKLICNE MATURE 2002/2003

Šolski center Velenje

Poklicna in tehniška šola za storitvene dejavnosti

Poklic:        ekonomski tehnik - PTI

                  gostinsko - turistični tehnik - PTI

Učitelj:      Jadranka Golčer, prof.

Špela Lukanc, prof.

                  Irena Zajc, prof.

1.         Naštej lastnosti računskih operacij v množici naravnih števil.

Primer :          a)

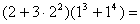
b)

 2.         Definiraj pojma praštevila in sestavljena števila ter navedi kriterije deljivosti

z 2, 3, 5, 9 in 10.

Primer :          Katero od naslednjih števil: 150, 986, 7440, 37440 in 88888 je deljivo z :

a) 2                 b) 3                 c) 5

3.         Definiraj največji skupni delitelj in najmanjši skupni večkratnik dveh celih števil. Kako ju lahko izračunamo? Kdaj sta dve števili tuji števili?

Primer :          a) D(120,144) =         b) v ( 120, 144) =

4.         Povej razloge za vpeljavo celih števil. Navedi osnovne računske operacije za računanje s celimi števili in njihove lastnosti.

Primer :          

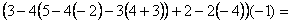
5.         Zapiši pravila za kvadriranje in kubiranje vsote in razlike dveh členov.

Primer:          

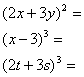
6.         Zapiši pravila za razstavljanje razlike kvadratov ter vsote in razlike kubov dveh

števil.

Primer:           Razstavi 

7.         Kako razcepimo tričlenike z uporabo Vietovega pravila?

Primer:           Razstavi tričlenike

8.         Naštej in utemelji pravila za računanje s potencami z naravnimi eksponenti.

Primer:          

9.         Kdaj, pri kakšnem imenovalcu, ulomek ni definiran? Kdaj sta dva ulomka enaka?

Primer :          Pri kateri vrednosti x ulomek  ne obstaja? 

Ugotovi ali sta ulomka  in  enaka?

10.       Povej razloge za vpeljavo racionalnih števil. Definiraj računske operacije z

racionalnimi števili.

Primer:          

11.       Opiši lastnosti računskih operacij v Q.

Primer :         

 12.       Kako seštevamo in odštevamo ulomke?

Primer:          

13.       Kako množimo in delimo ulomke?

Primer:          

14.       Definiraj potenco z negativnim celim eksponentom in naštej pravila za računanje s potencami s celimi eksponenti.

Primer :         

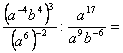
15.       Naštej računske operacije v R (realnih številih) in navedi njihove lastnosti.

Primer :          DELNO KORENJENJE                                *

Primer :          DELNO KORENJENJE                           *

16.       Naštej pravila za računanje s koreni.

Primer:          

17.       Kolikšna je vrednost potence a⁰ in kako zapišemo a^-1 z ulomkom?                     *

Primer:           POENOSTAVI IZRAZ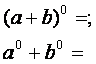

Primer:           POENOSTAVI IZRAZ ;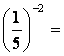

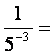
18.       Definiraj potenco s pozitivno osnovo in racionalnim eksponentom ter povej pravila za računanje s takimi potencami.

Primer:           a)

b) V obliki korena zapiši

19.       Definiraj linearno funkcijo. Kakšen je njen graf? Kako je odvisen od smernega koeficienta?

Primer:           Nariši graf funkcije .

20.       Kakšna sta grafa dveh linearnih funkcij z enakima smernima koeficientoma?

Primer:           Podano imaš premico . Določi enačbo vzporednice, ki gre skozi točko A(-4,2). Skiciraj.

21.       Zapiši enačbo linearne funkcije, katere graf poteka skozi dani točki A(x_1,y₁) in

B(x₂, y₂).

Primer :          Zapiši enačbo premice skozi točki  A(6, - 4) in B(- 2, 10). V kateri točki seka premica x  os? Kaj pa y os?

22.       Zapiši segmentno, eksplicitno in implicitno obliko enačbe premice!

Primer :          Dana je premica, ki od osi x odreže odsek 3, od osi y pa odsek 5. Zapiši jo v vseh treh oblikah!

23.       Kaj je rešitev sistema dveh linearnih enačb z dvema neznankama? Kako rešujemo sisteme dveh linearnih enačb z dvema neznankama?

Primer:            Reši sistem enačb:                             

24.       Kaj je naklonski kot premice? Kdaj sta premici vzporedni in kdaj pravokotni?

Primer :          Zapiši enačbo pravokotnice na premico  y = 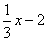, ki gre skozi točko

T (-4, 6). Izračunaj naklonski kot te premice!

25.       Kako izračunamo ploščino trikotnika z danimi oglišči A,B in C?

Primer:           Dan je trikotnik z oglišči A(3,-4), B(-2,5) in C(-1,1). Izračunaj ploščino tega trikotnika. Trikotnik nariši in ugotovi, kako je orientiran.

26.       Izpelji formulo za razdaljo med dvema danima točkama v koordinatnem sistemu.

Primer:           Točki A(5,-3) in B(1,0) nariši v isti koordinatni sistem in izračunaj razdaljo med njima.

27.       Kdaj sta dva trikotnika skladna? Naštej kriterije za skladnost trikotnikov.

Primer:           Načrtaj trikotnik s podatki in .

28.       Definiraj podobnost! Kdaj sta dva trikotnika podobna? Kaj velja za njune stranice?

Primer :          V trikotniku merijo stranice 3cm, 4cm in 5cm. Najkrajša stranica podobnega trikotnika je 8cm. Koliko merita ostali dve ?

29.       Opredeli pojme: sosedna kota, sokota, sovršna kota. Definiraj zunanje in notranje kote trikotnika.

Primer :          ;. Izračunaj še preostale notranje in zunanje kote tega trikotnika!

30.       Opredeli pojma komplementarna in suplementrana kota.

Primer:           Kotu  izračunaj komplementarni in suplementarni kot.

31.       Zapiši sinusni izrek in kdaj ga uporabljamo.

Primer :          Izračunaj neznane stranice  v trikotniku s podatki: a=10cm,

α = 82⁰ , β =45⁰ !

32.       S pomočjo Pitagorovega izreka izpelji formulo za višino in zapiši formulo za ploščino enakostraničnega trikotnika.

Primer :          Načrtaj enakostranični trikotnik s stranico a = 5cm. Načrtaj še simetrale vseh stranic. Opiši lastnosti presečišča simetral ?

33.       Opiši enakokraki trikotnik.

Primer :          Dan je enakokrak trikotnik z osnovnico o = 8cm in krakom k = 5cm. Izračunaj višino in ploščino tega trikotnika.

34.       Opredeli pojme v trikotniku: višina, simetrala stranice in simetrala kota.

Primer:           Izračunaj višino  v trikotniku: a=5cm, b=6cm in .

35.       Zapiši kosinusni izrek . Kdaj ga uporabljamo?

Primer :          Izračunaj stranico a in kot β  v trikotniku ABC s podatki: in .

36.       Zapiši Pitagorov izrek . Kdaj ga uporabljamo?

Primer:           Izračunaj stranico romba, če merita diagonali  in .

37.       Zapiši, kako vse lahko izračunamo ploščino trikotnika.

Primer:           V trikotniku so znane stranice in Izračunaj ploščino trikotnika.

38.       Definiraj paralelogram in naštej njegove lastnosti.

Primer:           Podan imaš paralelogram s podatki: ,  in . Izračunaj višino in ploščino paralelograma.

39.       Definiraj deltoid in naštej njegove lastnosti.

Primer:           Prva diagonala deltoida meri 16cm, druga pa je dvakrat krajša od prve. Izračunaj ploščino deltoida.

40.       Definiraj trapez in enakokraki trapez in naštej njune lastnosti. Kaj je srednica trapeza?

Primer:           Dan je enakokrak trapez z osnovnicama a = 16cm in c = 8cm ter krakom b= 12cm. Izračunaj kot ob osnovnici trapeza in ploščino trapeza..

41.       Definiraj romb. Opiši zvezo med stranico in diagonalama romba. Kaj je značilno za diagonali romba?                                               *

Primer :          V rombu s stranico 10cm in daljšo diagonalo 16cm izračunaj; kot, ki ga oklepata stranici romba in ploščino romba.

42.       Kaj je krog in kaj krožnica? Zapiši kako izračunamo obseg in ploščino kroga ter izpelji dolžino loka, ki pripada kotu a.

Primer:           Dan je krog s ploščino .Izračunaj obseg kroga.

43.       Opiši prizmo in utemelji formuli za prostornino in površino prizme. Kakšne tipe prizem poznaš?

Primer :          Izračunaj površino pravilne pokončne tristrane prizme z osnovnim robom

a = 4m in telesno višino v = 6m!

44.       Opiši  piramido in utemelji formuli za prostornino in površino piramide. Kakšne tipe piramid poznaš?

Primer :          Določi prostornino  pokončne pravilne tristrane piramide s telesno višino

v =8cm in stranico osnovne ploskve 

45.       Opiši krožni valj in utemelji formuli za prostornino in površino. Kdaj je valj enakostraničen?

Primer :          Polmer osnovne ploskve valja je r = 7cm. Kolikšna mora biti višina v, da bo prostornina V = 196 π cm³ ?

46.       Opiši stožec in utemelji formuli za prostornino in površino. Kolikšen je plašč tistega stožca, ki ima za osni presek enakostraničen trikotnik? Kako se imenuje?

Primer :          Izračunaj prostornino pokončnega stožca, če je njegova telesna višina enaka polmeru r osnovne ploskve!

47.       Zapiši splošno obliko kvadratne funkcije. Opiši pomen vodilnega koeficienta, prostega člena.

Primer :          Izračunaj ničli, teme, presečišče z osjo y  in nariši

48. Opiši pomen diskriminante kvadratne funkcije.

Primer: Nariši funkcijo

49.       Zapiši obliko kvadratne funkcije, iz katere sta razvidni ničli te kvadratne funkcije.

Primer :          Zapiši enačbo tiste kvadratne funkcije, ki ima ničli x₁= -2 in x₂ = 5 ter gre skozi točko A(1,2). Skiciraj!

50.       Zapiši temensko obliko kvadratne funkcije.

Primer:           Izračunaj teme in skiciraj kvadratno funkcijo

51.       Kaj je kvadratna funkcija? Kaj je njeno definicijsko območje? Naštej tri najpogostejše oblike enačbe kvadratne funkcije in opiši pomen posameznih konstant.

Primer:           Napiši enačbo kvadratne funkcije, če gre graf skozi točko , teme pa je v točki .

52.       Zapiši kvadratno enačbo! Kako jo rešimo? Kaj vpliva na rešljivost v R ?

Primer:           V množici realnih števil reši kvadratni enačbi in . Koliko rešitev imata? Zakaj?

53.       Povej Vietovi formuli za kvadratno enačbo .

Primer:           Zapiši kvadratno enačbo, ki ima rešitvi  in .

54.       Kako lahko določimo presečišča premice in parabol?

Primer:           Izračunaj v katerih točkah se sekata premica  in parabola !

55.       Kako lahko določimo presečišča parabol?

Primer:           Izračunaj v katerih točkah se sekata paraboli  in ! Skica!

 56.       Opiši, kako rešujemo kvadratne neenačbe.

Primer:           Reši kvadratni neenačbi  in

57.       Zapiši eksponentno funkcijo, skiciraj njen graf in povej njene osnovne lastnosti.

Primer :          Nariši v isti koordinatni sistem grafa eksponentnih funkcij in. Kakšna sta grafa?

 58.       Kako rešujemo eksponentne enačbe.

Primer:           Reši enačbo .

59.       Povej definicijo za logaritem . Kakšne vrednosti lahko zavzame x in z?

Primer :          Izračunaj x, če je

60.       Naštej pravila za računanje z logaritmi.

Primer :          Reši logaritemsko enačbo

61.       Definiraj polinom p(x) ter opiši osnovne računske operacije s polinomi. Kdaj sta dva polinoma enaka?

Primer             Naj bo in

Izračunaj vsoto in produkt polinomov p(x) in q(x).

62.       Definiraj polinom p(x) ter opiši osnovne računske operacije s polinomi.

Primer             Naj bo in

Izračunaj količnik polinomov p(x) in q(x).

63.       Kako delimo polinom z linearnim polinomom.

Primer :          Naj bo in

Izračunaj količnik p(x) : q(x).

64.       Pojasni uporabnost Hornerjevega algoritma.

Primer : Izračunaj ničle polinoma

 65.       Pojasni uporabnost Hornerjevega algoritma.

Primer:           S pomočjo Hornerjevega algoritma deli polinom  s polinomom .

 66.       Kaj je ničla polinoma? Koliko ničel ima polinom n-te stopnje?

Primer :          Preveri ali je  ničla danega polinoma Ali je tudi dvakratna ničla? Izračunaj še ostale ničle tega polinoma.

67.       Razloži potek risanja grafa polinoma.

Primer :          Skiciraj graf polinoma

 68.       Definiraj racionalno funkcijo. Kaj je ničla, kaj pol in kaj asimptota racionalne funkcije?

Primer :          Nariši graf 

 69.       Kako se obnaša graf racionalne funkcije v ničlah in polih lihe ali sode stopnje?

Primer :          Nariši graf 

70.       Definiraj kotne funkcije v pravokotnem trikotniku s katetama a in b ter hipotenuzo c.

Primer :          Dan je pravokotni trikotnik s kateto b =6cm in kotom α = 30⁰.  Izračunaj hipotenuzo c in kot β!

71.       Zapiši osnovne zveze med kotnimi funkcijami.

Primer.           Naj bo  in kot  naj leži v 2. kvadrantu. Izračunaj  in .

72.       Definiraj funkcijo , za poljuben kot (enotska krožnica), nariši njen graf in povej njene lastnosti!

Primer:           Nariši

73.       Definiraj funkcijo  za poljuben kot ( enotska krožnica), nariši njen graf in povej njene lastnosti!

Primer :          Izračunaj, kje ima ničle funkcija .

74.       Ali so funkcije ,  in  sode ali lihe. Kakšna je njihova perioda?

Primer:           Poenostavi

 75.       Zapiši adicijska izreka za sinus vsote in razlike.

Primer:           Poenostavi z uporabo adicijskih izrekov .

76.       Zapiši adicijska izreka za kosinus vsote in razlike.

Primer:           Poenostavi z uporabo adicijskih izrekov .

 77.       Zapiši osnovne zveze med kotnimi funkcijami in formule za kotne funkcije dvojnih kotov.

Primer:           Izračunaj, če je  in  kot x v tretjem kvadrantu.

78.       Kaj je zaporedje? Kdaj narašča ( pada), kdaj je omejeno? Spodnja in zgornja meja.

Primer :          Kakšno (naraščajoče, padajoče, omejeno, neomejeno) je zaporedje s splošnim členom 

79.       Kdaj je zaporedje aritmetično? Zapiši splošni člen aritmetičnega zaporedja.

Primer :          Sedmi člen AZ je 21, tretji pa . Poišči petnajsti člen tega zaporedja!

80.       Kdaj je zaporedje aritmetično? Zapiši formulo za vsoto prvih n členov aritmetičnega zaporedja.

Primer:         Vsota prvih dvanajstt členov AZ z diferenco – 3 je 66. Določi vsoto petnajstih členov AZ!

81.       Kdaj je zaporedje geometrijsko? Zapiši splošni člen geometrijskega zaporedja.

Primer:             Za kateri x so x+5, 25 - x, 30 + 2x členi geometrijskega zaporedja ? Izračunaj osmi tega člen zaporedja.

82.       Kdaj je zaporedje geometrijsko? Zapiši formulo za vsoto prvih n členov geometrijskega zaporedja.

Primer:            Vsota prvih pet členov GZ s količnikom 2 je 252. Določi četrti člen GZ!

83.       Zapiši formulo za obrestno-obrestno obrestovanje glavnice a po n letih pri letni

obrestni meri p in pri letnem pripisu obresti.

Primer :          Znesek 200 000 tolarjev vložimo na banko in pustimo, da se šestdesetkrat obrestuje po 0,4% mesečni obrestni meri in mesečnemu pripisu obresti. Koliko denarja lahko potem  dvignemo z obrestmi vred?

84.       S pomočjo številske premice izpelji, kolikšen znesek privarčujemo v n letih, če na začetku vsakega leta položimo znesek a.

Primer:           Na začetku vsakega leta vložimo 50 000 SIT po letni obrestni meri p = 10%. Koliko lahko z obrestmi vred dvignemo po desetih letih?

85.       Opiši kako na konformni in na relativni način preračunavamo obresti.

Primer:           V času inflacije je polletna obrestna mera 80%. Izračunaj mesečno obrestno mero na konformni in na relativni način.

86.       Naštej osnovne statistične pojme in jih obrazloži!

Primer:           Na POP TV jih je zanimalo, katere oddaje Slovenci najraje gledamo. Povprašali so 110 mimoidočih na Čopovi ulici. Obrazloži statistične pojme na tem primeru.

87.       Katere grafične prikaze poznamo? Opiši kako prikažemo podatke v obliki paličnega diagrama.

Primer :           V razredu z 32 dijaki so 3  dijaki odlični, 6 prav dobrih, 15 dijakov dobrih,

5 zadostnih, ostali pa nezadostni.Podatke prikaži v obliki paličnega diagrama.

88.       Kaj pove relativna frekvenca in kako jo izračunamo! Na kakšne načine lahko izrazimo relativno frekvenco?

Primer:           Na šoli zaključuje šolanje 40 dijakov. 5 se vpisujejo v maturitetni tečaj,16 jih bo nadaljevalo šolanje na visoki šoli, 6 na višji šoli, 4 gredo v vojsko, 6 se jih namerava takoj zaposliti, ostali še ne vedo, kaj bodo počeli.Podatke prikaži v tabeli in izračunaj relativne frekvence.

89.       Katere grafične prikaze poznamo? Opiši kako prikažemo podatke v obliki frekvenčnega kolača.

Primer:           Na šoli je bilo 24 dijakov ocenjenih negativno. 10 jih je imelo eno negativno oceno,7 dve negativni oceni, 4 tri negativne ocene, ostali pa več kot tri negativne ocene. Podatke prikaži v obliki frekvenčnega kolača.

90.       Kaj je aritmetična sredina, kaj mediana ali središčnica in kaj modus ali goriščnica?

Primer:           Paličasti diagram prikazuje rezultate pisnega ocenjevanja znanja iz matematike 4.a razreda.Koliko je dijakov v razredu? Kolikšna je povprečna ocena?Določi mediano in modus!