Vectors in two dimensions

1. In the triangle $\mathrm{△}ABC$ point $P$ is the midpoint of the segment $BC$. Write the following vectors in terms of vectors $\mathbf{a}=\overrightarrow{AB}$ and $\mathbf{b}=\overrightarrow{AC}$:
   

   (a)   $\overrightarrow{CB}$

   (b)   $\overrightarrow{PC}$

   (c)   $\overrightarrow{AP}$

   Solutions:    (a)  $\overrightarrow{CB}=\mathbf{a}-\mathbf{b}$;     (b)  $\overrightarrow{PC}=-\frac{1}{2}\mathbf{a}+\frac{1}{2}\mathbf{b}$;     (c)  $\overrightarrow{AP}=\frac{1}{2}\mathbf{a}+\frac{1}{2}\mathbf{b}$
2. The point $S$ is the center of the regular hexagon $ABCDEF$. Write the following vectors as linear combinations of vectors $\mathbf{a}=\overrightarrow{AB}$ and $\mathbf{b}=\overrightarrow{BC}$:
   

   (a)   $\overrightarrow{AC}$

   (b)   $\overrightarrow{ES}$

   (c)   $\overrightarrow{FC}$

   (d)   $\overrightarrow{EA}$

   Solutions:    (a)  $\overrightarrow{AC}=\mathbf{a}+\mathbf{b}$;     (b)  $\overrightarrow{ES}=\mathbf{a}-\mathbf{b}$;     (c)  $\overrightarrow{FC}=2\mathbf{a}$;     (d)  $\overrightarrow{EA}=\mathbf{a}-2\mathbf{b}$
3. In the rectangle $ABCD$ point $P$ is the midpoint of the side $CD$. Points $U$ and $V$ divide the side $BC$ into three equal parts. Express the following vectors as linear combinations of given vectors $\mathbf{a}=\overrightarrow{AB}$ and $\mathbf{b}=\overrightarrow{AD}$:
   

   (a)   $\overrightarrow{AC}$

   (b)   $\overrightarrow{BD}$

   (c)   $\overrightarrow{AP}$

   (d)   $\overrightarrow{AU}$

   (e)   $\overrightarrow{PV}$

   Solutions:    (a)  $\overrightarrow{AC}=\mathbf{a}+\mathbf{b}$;     (b)  $\overrightarrow{BD}=-\mathbf{a}+\mathbf{b}$;     (c)  $\overrightarrow{AP}=\frac{1}{2}\mathbf{a}+\mathbf{b}$;     (d)  $\overrightarrow{AU}=\mathbf{a}+\frac{1}{3}\mathbf{b}$;     (e)  $\overrightarrow{PV}=\frac{1}{2}\mathbf{a}-\frac{1}{3}\mathbf{b}$
4. In the square $ABCD$ point $P$ is the midpoint of the side $BC$. Express the following vectors as linear combinations of basis vectors $\mathbf{a}=\overrightarrow{AC}$ and $\mathbf{b}=\overrightarrow{AD}$:
   

   (a)   $\overrightarrow{AB}$

   (b)   $\overrightarrow{DB}$

   (c)   $\overrightarrow{PD}$

   Solutions:    (a)  $\overrightarrow{AB}=\mathbf{a}-\mathbf{b}$;     (b)  $\overrightarrow{DB}=\mathbf{a}-2\mathbf{b}$;     (c)  $\overrightarrow{PD}=-\mathbf{a}+\frac{3}{2}\mathbf{b}$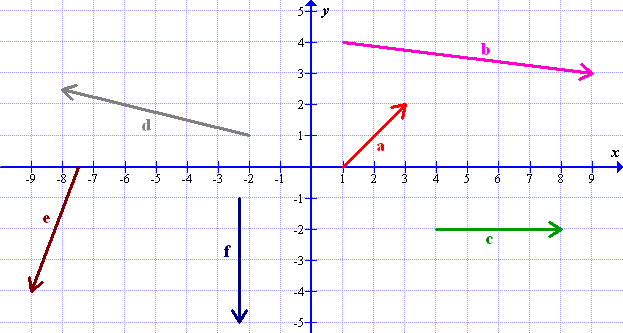
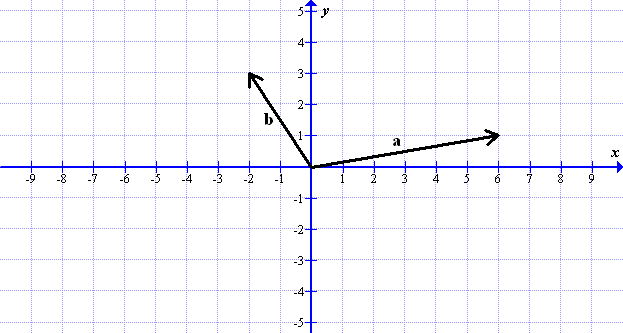
5. Write the vectors shown in the diagram bellow in column vector notation.
   

   

   Solutions:    $\mathbf{a}=\left(\begin{array}{c}2\\ 2\end{array}\right)$,     $\mathbf{b}=\left(\begin{array}{c}8\\ -1\end{array}\right)$,     $\mathbf{c}=\left(\begin{array}{c}4\\ 0\end{array}\right)$,     $\mathbf{d}=\left(\begin{array}{c}-6\\ \frac{3}{2}\end{array}\right)$,     $\mathbf{e}=\left(\begin{array}{c}-\frac{3}{2}\\ -4\end{array}\right)$,     $\mathbf{f}=\left(\begin{array}{c}0\\ -4\end{array}\right)$
6. Write the vectors shown in the diagram bellow in terms of standard basis vectors $\mathbf{i}$ and $\mathbf{j}$.
   

   

   Solutions:    $\mathbf{a}=2\mathbf{i}+3\mathbf{j}$,     $\mathbf{b}=6\mathbf{i}-3\mathbf{j}$,     $\mathbf{c}=-\mathbf{i}+6\mathbf{j}$,     $\mathbf{d}=-5\mathbf{i}$,     $\mathbf{e}=6\mathbf{j}$,     $\mathbf{f}=-7\mathbf{i}-3\mathbf{j}$
7. Vectors $\mathbf{a}$ and $\mathbf{b}$ are shown in the diagram bellow.
   

   

   (a)   Draw vectors  $\mathbf{a}+\mathbf{b}$  and  $\mathbf{a}-\mathbf{b}$.

   (b)   Write vectors $\mathbf{a}$ and $\mathbf{b}$ in column notation.

   (c)   Calculate vectors  $\mathbf{a}+\mathbf{b}$  and  $\mathbf{a}-\mathbf{b}$ and write them in column notation.

   Solutions:    (b)  $\mathbf{a}=\left(\begin{array}{c}6\\ 1\end{array}\right)$,     $\mathbf{b}=\left(\begin{array}{c}-2\\ 3\end{array}\right)$;     (c)  $\mathbf{a}+\mathbf{b}=\left(\begin{array}{c}4\\ 4\end{array}\right)$,     $\mathbf{a}-\mathbf{b}=\left(\begin{array}{c}8\\ -2\end{array}\right)$
8. Vectors $\mathbf{a}$ and $\mathbf{b}$ have the coordinates:  $\mathbf{a}=\left(\begin{array}{c}10\\ 6\end{array}\right)$,    $\mathbf{b}=\left(\begin{array}{c}6\\ 9\end{array}\right)$.
   Calculate vectors:
   

   (a)   $\mathbf{u}=\mathbf{a}+\mathbf{b}$

   (b)   $\mathbf{v}=5\mathbf{a}-6\mathbf{b}$

   (c)   $\mathbf{w}=-\frac{1}{2}\mathbf{a}+\frac{2}{3}\mathbf{b}$

   Solutions:    (a)  $\mathbf{u}=\left(\begin{array}{c}16\\ 15\end{array}\right)$;     (b)  $\mathbf{v}=\left(\begin{array}{c}14\\ -24\end{array}\right)$;     (c)  $\mathbf{w}=\left(\begin{array}{c}-1\\ 3\end{array}\right)$
9. Given vectors $\mathbf{a}=4\mathbf{i}-3\mathbf{j}$ and $\mathbf{b}=5\mathbf{i}+\frac{3}{2}\mathbf{j}$ calculate:
   

   (a)   $\mathbf{u}=\mathbf{a}+2\mathbf{b}$

   (b)   $\mathbf{v}=-\mathbf{a}+4\mathbf{b}$

   (c)   $\mathbf{w}=\frac{1}{2}\mathbf{a}-\mathbf{b}$

   Solutions:    (a)  $\mathbf{u}=14\mathbf{i}$;     (b)  $\mathbf{v}=16\mathbf{i}+9\mathbf{j}$;     (c)  $\mathbf{w}=-3\mathbf{i}-3\mathbf{j}$
10. Given vector $\mathbf{a}=\left(\begin{array}{c}8\\ 6\end{array}\right)$ calculate:
    

    (a)   $\frac{5}{2}\mathbf{a}$

    (b)   $2\mathbf{a}+3\mathbf{i}-\mathbf{j}$

    (c)   $|\mathbf{a}|$

    Solutions:    (a)  $\frac{5}{2}\mathbf{a}=\left(\begin{array}{c}20\\ 15\end{array}\right)$;     (b)  $2\mathbf{a}+3\mathbf{i}-\mathbf{j}=\left(\begin{array}{c}19\\ 11\end{array}\right)$;     (c)  $|\mathbf{a}|=10$
11. Let $\mathbf{a}=\left(\begin{array}{c}21\\ 72\end{array}\right)$ and $\mathbf{b}=\left(\begin{array}{c}42\\ -56\end{array}\right)$.
    

    (a)   Find $|\mathbf{a}|$ and $|\mathbf{b}|$.

    (b)   Calculate $\mathbf{c}=\mathbf{a}+\mathbf{b}$.

    (c)   Find $|\mathbf{c}|$.

    Solutions:    (a)  $|\mathbf{a}|=75,|\mathbf{b}|=70$;     (b)  $\mathbf{c}=\left(\begin{array}{c}63\\ 16\end{array}\right)$;     (c)  $|\mathbf{c}|=65$
12. Let $\mathbf{a}=\left(\begin{array}{c}6\\ 8\end{array}\right)$.
    

    (a)   Find $|\mathbf{a}|$.

    (b)   Write down the unit vector $\mathbf{u}$ which has the direction of the vector $\mathbf{a}$.

    Solutions:    (a)  $|\mathbf{a}|=10$;     (b)  $\mathbf{u}=\left(\begin{array}{c}\frac{3}{5}\\ \frac{4}{5}\end{array}\right)$
13. Let $\mathbf{a}=\left(\begin{array}{c}-5\\ 12\end{array}\right)$.
    Find the unit vector in the direction of the vector $\mathbf{a}$ and write it in terms of $\mathbf{i}$ and $\mathbf{j}$.
    Solutions:    $\mathbf{u}=-\frac{5}{13}\mathbf{i}+\frac{12}{13}\mathbf{j}$
14. Consider vectors ${\mathbf{u}}_1=\frac{1}{2}\mathbf{i}+\frac{\sqrt{3}}{2}\mathbf{j}$ and ${\mathbf{u}}_2=\left(\begin{array}{c}-1\\ 0\end{array}\right)$.
    

    (a)   Show that ${\mathbf{u}}_1$ and ${\mathbf{u}}_2$ are unit vectors.

    (b)   Calculate $|{\mathbf{u}}_1-{\mathbf{u}}_2|$ (write the exact value).

    Solutions:    (a)  $|{\mathbf{u}}_1|=1,|{\mathbf{u}}_2|=1$;     (b)  $|{\mathbf{u}}_1-{\mathbf{u}}_2|=\sqrt{3}$
15. Points $A$ and $B$ have coordinates $A(3,1),B(5,6)$.
    

    (a)   Write down the position vectors $\overrightarrow{OA}$ and $\overrightarrow{OB}$.

    (b)   Find the vector $\overrightarrow{AB}$.

    Solutions:    (a)  $\overrightarrow{OA}=\left(\begin{array}{c}3\\ 1\end{array}\right)$,    $\overrightarrow{OB}=\left(\begin{array}{c}5\\ 6\end{array}\right)$;     (b)  $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\left(\begin{array}{c}2\\ 5\end{array}\right)$
16. Points $A(-2,1),B(5,4)$ and $C(3,8)$ are vertices of a triangle.
    

    (a)   Find vectors $\mathbf{u}=\overrightarrow{AB}$,   $\mathbf{v}=\overrightarrow{BC}$ and $\mathbf{w}=\overrightarrow{CA}$.

    (b)   Verify that $\mathbf{u}+\mathbf{v}+\mathbf{w}=\mathbf{0}$.

    Solutions:    (a)  $\mathbf{u}=\left(\begin{array}{c}7\\ 3\end{array}\right)$,    $\mathbf{v}=\left(\begin{array}{c}-2\\ 4\end{array}\right)$,    $\mathbf{w}=\left(\begin{array}{c}-5\\ -7\end{array}\right)$;     (b)  $\mathbf{u}+\mathbf{v}+\mathbf{w}=\left(\begin{array}{c}0\\ 0\end{array}\right)$
17. Points $A(2,3),B(9,5)$ and $C(10,9)$ are three of the vertices of the parallelogram $ABCD$.
    

    (a)   Find the coordinates of point $D$.

    (b)   Find the length of the diagonal $AC$

    Solutions:    (a)  $D(3,7)$;     (b)  $|\overrightarrow{AC}|=10$
18. Points $A(-3,1),B(5,4)$ and $D(-1,6)$ are three of the vertices of the parallelogram $ABCD$.
    

    (a)   Find the coordinates of point $C$.

    (b)   Find the coordinates of the intersection point of the diagonals $AC$ and $BD$.

    Solutions:    (a)  $C(7,9)$;     (b)  $P(2,5)$
19. Points $A(6,1)$ and $B(16,5)$ are two of the vertices of the parallelogram $ABCD$. Point $M(13,8)$ is the midpoint of the side $CD$. Point $P$ is the intersection point of the diagonals.
    

    (a)   Find the coordinates of points $C$ and $D$.

    (b)   Find the coordinates of point $P$.

    Solutions:    (a)  $C(18,10),D(8,6)$;     (b)  $P(12,5.5)$
20. Points $A(-5,0),B(22,-3),C(19,10)$ and $D(-8,13)$ are the vertices of the quadrilateral $ABCD$.
    

    (a)   Show that $ABCD$ is a parallelogram.

    (b)   Find the coordinates of the point $P$ which is the intersection point of the diagonals.

    (c)   Find the length of the longer diagonal.

    Solutions:    (a)  $\overrightarrow{AB}=\overrightarrow{DC}=\left(\begin{array}{c}27\\ -3\end{array}\right)$ and $\overrightarrow{AD}=\overrightarrow{BC}=\left(\begin{array}{c}-3\\ 13\end{array}\right)$;     (b)  $P(7,5)$;     (c)  $|\overrightarrow{BD}|=34$
21. A given line segment $AB$ has the endpoints $A(2,1)$ and $B(8,10)$. Points $U$ and $V$ divide the segment $AB$ in three equal parts. Find the coordinates of the points $U$ and $V$.
    Solutions:    $U(4,4),V(6,7)$
22. Line segment $AB$ has the endpoints $A(-3,2)$ and $B(7,17)$. $T$ is the point on $AB$ such that $AT:TB=2:3$. Find the coordinates of the point $T$.
    Solutions:    $T(1,8)$
23. Points $A(5,20)$ and $B(41,-4)$ are the endpoints of the line segment $AB$.
    

    (a)   Find the coordinates of the point $U$ on $AB$ such that $AU:UB=1:3$.

    (b)   Find the coordinates of the point $V$ on $AB$ such that $AV:AB=1:3$.

    Solutions:    (a)  $U(14,14)$;     (b)  $V(17,12)$
24. $M(22,31)$ is a point on the line segment $AB$ such that $AM:MB=2:5$. Given the point $A(4,3)$ find the coordinates of the point $B$.
    Solutions:    $B(67,101)$
25. Points $B(17,5),C(25,21)$ and $D(13,17)$ are three of the vertices of the parallelogram $ABCD$. $P$ is the point on $AB$ such that $AP:PB=1:3$, and $R$ is the point on $AD$ such that $AR:RD=1:3$.
    

    (a)   Find the coordinates of the point $A$.

    (b)   Find the coordinates the points $P$ and $R$.

    (c)   Write down the coordinates the vector $\overrightarrow{PR}$.

    (d)   Show that the vector $\overrightarrow{PR}$ is parallel to the vector $\overrightarrow{BD}$.

    Solutions:    (a)  $A(5,1)$;     (b)  $P(8,2),R(7,5)$;     (c)  $\overrightarrow{PR}=\left(\begin{array}{c}-1\\ 3\end{array}\right)$;     (d)  $\overrightarrow{BD}=4\cdot \overrightarrow{PR}$
26. Consider vectors $\mathbf{a}=\left(\begin{array}{c}5\\ 3\end{array}\right)$,   $\mathbf{b}=\left(\begin{array}{c}1\\ -2\end{array}\right)$ and $\mathbf{c}=\left(\begin{array}{c}15\\ -4\end{array}\right)$. Express vector $\mathbf{c}$ in terms of $\mathbf{a}$ and $\mathbf{b}$.
    Solutions:    $\mathbf{c}=2\mathbf{a}+5\mathbf{b}$
27. Consider vectors $\mathbf{u}=\left(\begin{array}{c}8\\ 3\end{array}\right)$,   $\mathbf{v}=\left(\begin{array}{c}-2\\ 7\end{array}\right)$ and $\mathbf{w}=\left(\begin{array}{c}13\\ 1\end{array}\right)$. Express vector $\mathbf{w}$ in terms of $\mathbf{u}$ and $\mathbf{v}$.
    Solutions:    $\mathbf{w}=\frac{3}{2}\mathbf{u}-\frac{1}{2}\mathbf{v}$
28. Consider vectors $\mathbf{a}=\left(\begin{array}{c}2\\ -3\end{array}\right)$ and $\mathbf{b}=\left(\begin{array}{c}-1\\ 2\end{array}\right)$. Write vector $\mathbf{i}$ in terms of $\mathbf{a}$ and $\mathbf{b}$.
    Solutions:    $\mathbf{i}=2\mathbf{a}+3\mathbf{b}$
29. Consider vectors $\mathbf{u}=\left(\begin{array}{c}6\\ 9\end{array}\right)$,   $\mathbf{v}=\left(\begin{array}{c}4\\ 6\end{array}\right)$ and $\mathbf{w}=\left(\begin{array}{c}8\\ 10\end{array}\right)$.
    

    (a)   Express vector $\mathbf{u}$ in terms of $\mathbf{v}$ and $\mathbf{w}$ if possible.

    (b)   Express vector $\mathbf{w}$ in terms of $\mathbf{u}$ and $\mathbf{v}$ if possible.

    Solutions:    (a)  $\mathbf{u}=\frac{3}{2}\mathbf{v}+0\mathbf{w}$;     (b)  It's not possible.
30. Vector $\mathbf{a}=\left(\begin{array}{c}12\\ m\end{array}\right)$ has the modulus $|\mathbf{a}|=13$. Find the value of $m$. Write down all possible solutions.
    Solutions:    $m_1=5,m_2=-5$

 Index