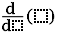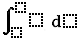Tips for using TI-nspire

Tips for using TI-nspire

Basic calculations

Copy-Paste: You can use touchpad to move to one of the previous calculations and highlight this calculation (or a part of it). Then press ctrl c to copy. After doing so move the cursor down to the active input line and press ctrl v to paste the copied content.
Substituting a given value into an expression: Given an algebraic expression including a variable, you can evaluate this expression using the operator | (vertical line) followed by the name of this variable and the numeric value (e.g. $e x p r e s s i o n | x = 2$ ). Example:
Calculation $3 x^{2} + 5 x - 1 | x = 2$ returns the result 21.
You can use this in combination with copy-paste to evaluate a given expression for several values of x.
The

TEMPLATES button: You will find this button to the right of number 9. This button shows you several templates = patterns prepared for calculations. You'll find templates for log_b a, degrees-minutes-seconds, definite integral, derivative at a given point and many others.
The

CATALOG button (book button): You will find this button to the right of TEMPLATES button. This button shows you the list of all functions available on your calculator. In addition: pressing ctrl CATALOG shows you the list of all special symbols.
Storing value into a variable: Result you've just calculated can be stored for further calculations. You can do it by assigning this value to a variable. To do this press ctrl sto→ and type the name of the variable, e.g. abc. Example:
Calculation 12 + 34 returns the result 46. Press ctrl sto→ abc to store it. In further calculations you can use the variable abc, e.g. calculation abc + 4 returns the result 50.
Operators := and =: can be used for assigning value to a variable, too. Colon (:) must be written on the same side as the name of the variable. Example:
123 =: aaa
bbb := 456
The ans function: The last result you've calculated is stored into a special variable called ans (answer). To use this value in further calculations press ans (in fact ctrl ans) or simply type letters a n s. Example:
Calculation $12^{2} + 5^{2}$ has the result 169. Immediately after calculating it, you want to find the square root of this result. Enter $\sqrt{ans}$ and the final result is 13.
Entering function names: You can use typing letters for entering the names of many other functions.
- Functions sin, cos, tan can be obtained using the trig button, but using letters s i n, c o s, t a n works fine, too.
- Base 10 logarithm can be entered typing letters l o g. For a general base logarithm (log_ax) use the log button or find the appropriate template using the TEMPLATES button.
Some special functions: Use letters to enter the names of the following functions:
- factor(n) = returns the prime factorization of n
- gcd(m,n) = returns the greatest common divisor of given numbers
- lcm(m,n) = returns the least common multiple of given numbers
- nCr(n,r) = returns n choose r = $(\binom{n}{r})$
- isPrime(n) = returns "true" if n is a prime number (warning: this function is disabled in exam mode – I hope you will not need it during an exam)
Mixed numbers are numbers made of two parts: an integer part and a proper fraction. Number $4 \frac{1}{3}$ means "four and one third". To enter this number you should type it as   $(4 + \frac{1}{3})$ . You should never omit the plus simbol between the integer part and the fraction. If you omit the plus your calculator will assume there's multiplication and the result will be wrong.
Results of calculations are normally displayed as improper fractions. If you want to write a result as a mixed number, use the propFrac function. To get this function press menu ► Number ► Fraction Tools ► Proper Fraction or simply type the name using letters. Example:
Calculate the square of $2 \frac{1}{2}$ by entering   $(2 + \frac{1}{2})^{2}$ and the result will be dispalyed as   $\frac{25}{4}$ .
Now type   propFrac(ans) and the result will be converted to   $6 + \frac{1}{4}$ .
Using

the Σ symbol for sums: To calculate the sum of a finite number of terms of a sequence use the Σ template. Press TEMPLATES button and select Σ template, then enter the values. Example:
Calculation $\sum_{n = 1}^{7} (n^{2})$ returns the result 140, which represents the sum of the first seven terms of the sequence $u_{n} = n^{2}$ .

Degrees and radians

When calculating with angles, you can use degrees or radians.

The calculator's main setting is accessed using on ► Settings ► Document Settings ► Angle. This setting sets the angle units for calculations.
(Warning: On certain calculators OK sets this setting only for one document. If there's a Make Default button, click this to activate the setting for all documents and the scratchpad.)
You can specify different angular units for graphs. On Graphs page press menu ► Settings ► Graphing Angle.

In Math AI SL course radians are not required, so I recommend you to set both settings to degrees.

In all other IB courses (Math AI HL, Math AA SL and Math AA HL) you must know how to calculate in degrees and in radians.
You can select degrees for both: calculations and graphs, but this is not recommended.
It's possible to select degrees for calculations and radians for graphs, but this is not recommended either.
I recommend you to select radians for both: calculations and graphs. When radians are selected, you will still be able to calculate with degrees (and minutes and seconds) if you use the ° ' '' symbols. Enter the angle using ° ' '' symbols and the calculator will convert the angle to radians automatically.

Calculation

\sin (30^{\circ})

returns the result 0.5.

Calculation

30^{\circ} + 60^{\circ}

returns the result 1.5708, which is the correct result in radians. You can convert it to degrees using the command Ans►DD ("Decimal Degrees") or Ans►DMS ("Degrees-Minutes-Seconds").

Additional help:

Use π► button (to the left of letter H) to enter the degrees symbol ° and the minutes symbol '. For seconds use the minutes symbol twice. Alternatively: you can use the degrees-minutes-seconds template °'''.
You'll find functions ►DD ("Decimal Degrees") and ►DMS ("Degrees-Minutes-Seconds") in the CATALOG. Alternatively: you can type them as @>DD and @>DMS. You'll find the symbol @ in the list of all symbols – press ctrl CATALOG.

Solving equations

You can use the following functions to solve simple equations and systems of simultaneous equations.

Function nSolve solves the given equation numerically. You must write the equation and specify the name of the variable. It can be used for equations in one variable and it returns one of the solutions. Warning: If a given equation has multiple solutions this function will not show all the solutions. I recommend you to use graphical mode to solve equations with multiple solutions.
Calculation $nSolve (x^{2} - x - 6, x)$ returns the result −2, which is one of the solutions, but it won't show the other solution $x = 3$ .
Function polyRoots finds roots (zeros) of a polynomial. You must write the polynomial and the name of the variable. It's also possible to write all the coefficients – in this case you must write them in curly brackets and omit the name of the variable. Function polyRoots will find all real zeros (for complex zeros use cPolyRoots). Examples:
Calculation   $polyRoots (x^{2} - x - 6, x)$    returns the result   ${- 2, 3}$ .

Calculation   $polyRoots ({1, 3, 3, 1})$    returns the result   ${- 1, - 1, - 1}$ .

Calculation   $cPolyRoots (x^{2} + 1, x)$    returns complex roots   ${- i, i}$ .
Function linSolve finds solution of a system of simultaneous linear equations. You can use different notations. In all variants you must write the equations and the names of variables. Examples of notation:
$linSolve (x + y = 3 and x - y = 1, x, y)$

$linSolve (x + y = 3 and x - y = 1, {x, y})$

$linSolve ({x + y = 3, x - y = 1}, {x, y})$

$linSolve ({\begin{matrix} x + y = 3 \\ x - y = 1 \end{matrix}, {x, y})$
The last notation is obtained using the TEMPLATES button. In all cases calculator returns the result ${2, 1}$ , meaning that $x = 2, y = 1$ .

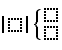
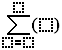
Graphs

Warning: Some of the functions described here are not available in the scratchpad mode. You must open a document with graphs page to use them.

Coordinate grid: When on the graphs page, press menu ► View ► Grid.
Table of the given function: When on the graphs page, press menu ► Table ► Split-Screen Table. When the table is displayed, you can use menu ► Actions to adjust the display mode. Use menu ► Table ► Edit Table Settings to change the initial value and step.
Window settings: If coordinate system units on the screen are too small or too big, I recommend you to change them using menu ► Window/Zoom ► Window Settings. A dialog box will appear:

XMin:   -7.12345

XMax:   7.12345

XScale:   Auto

YMin:   -5.12345

YMax:   5.12345

YScale:   Auto

              OK Cancel
You can use this dialog box to change which part of the graph is displayed (adjust XMin, XMax, YMin and YMax values).
Besides you can decide which units will be shown. Settings XScale and YScale determine which units are shown. Try replacing "Auto" setting by number 1 or some other number to select your own units.
Don't forget to press OK button at the end.
Special points on the graph: Draw the graph first. Then press menu ► Analyze Graph. Then select what you're looking for: zeros, maxima, minima, intersection points etc. For each point you must specify an interval (CLICK for "lower bound" and "upper bound").
Moving labels: Labels corresponding to graphs and points are very useful, but sometimes you'll want to move them. To do it, first move the cursor over the label. Cursor has the shape of a "hand" which is open (at the beginning). Hold CLICK for a few seconds (or use ctrl CLICK) to close the "hand". Now you have the grip and you can move this label using cursors. CLICK again to release the label.
Area between two curves: Draw graphs of two functions. Then press menu ► Analyze Graph ► Bounded Area. When selecting the lower and upper bound CLICK exactly on the intersection point (words "intersection point" must be written on the screen when clicking).
Connection between graphic mode and calculator mode: A function defined in graphic mode as f1(x) can be used in calculator mode with the same name. Use function names to avoid repetitive typing of long function equations. Example:
First draw the graf of the function $f1 (x) = x^{3} - 2 x^{2} - 4 x + 8$ . Now you can calculate the definite integral of this function simply as $\int_{- 2}^{2} f1 (x) d x$ and it returns the result 21.3333.
Tool hints: When using a special tool in graphic mode, a small square appears in the upper left corner of the display. This square is visible when the tool is active. Moving cursor over this square shows additional hints.
Point on a graph: Draw the graph of the given function. Then press menu ► Geometry ► Points and Lines ► Point On. Select the graph and the point on it. Use esc to close the point selection tool (the square indicating this tool disappears). Now you can apply different actions to this point:
- You can use the "hand" to move the point along the graph.
- You can click on one of the coordinates to highlight it. Than you can increase or decrease the number of decimals by pressing + and − buttons.
- When a coordinate is highlighted, you can store the value to a variable. Press ctrl sto→. Label var:=1234 appears. Replace var by the name of a variable, e.g.: aaa and press enter. Now you can use this variable in all calculations in this document.
  Warning: In other documents and in the scratchpad mode a variable with the same name can have a different value.
- When a coordinate is highlighted, you can change its value and move the point to a new position. CLICK the highlighted coordinate again and a small frame will appear. Enter the value in this frame and press enter.
Drawing several graphs at the same time: Sometimes you want to investigate properties of a graph at different values of a certain parameter. You can draw several graphs at the same time if you write down all parameter values in the form of a set (in curly brackets). Example:
In graphic mode enter the function $f (x) = x^{2} + {1, 2, 3}$ and your GDC will draw three functions at the same time: $f (x) = x^{2} + 1$ , $f (x) = x^{2} + 2$ and $f (x) = x^{2} + 3$ .

Derivatives and integrals

The

derivative template: Press TEMPLATES button to obtain the derivative template. TI-nspire CX calculator can not calculate the derivative in general (as a function of x), but it can calculate the derivative at a given point. To specify the point you must add the operator | (vertical line) and specify the value of x. Example:
Calculation $\frac{d}{d x} (\sqrt{x + 1}) | x = 3$ returns the result $\frac{1}{4}$ . This result is the derivative of the function $f (x) = \sqrt{x + 1}$ at $x = 3$ .
The

integral template: Press TEMPLATES button to obtain the integral template. TI-nspire CX calculator can not calculate indefinite integrals, so this template can be used only for definite integrals. Example:
Calculation $\int_{0}^{15} \sqrt{x + 1} d x$ returns the result 42. This result is the definite integral of the function $f (x) = \sqrt{x + 1}$ on the interval from $x = 0$ to $x = 15$ .

Binomial distribution and normal distribution

TI-nspire has several built-in function to calculate probabilities connected with the binomial and normal distribution: binomPdf, binomCdf, normCdf, etc. You can use these functions in three different ways:

You can simply use letters to type the name of a certain function, e.g.: b i n o m p d f . After entering the name of the function you must type the corresponding values in correct order (you must memorize that the first parameter is the number of trials, the second is probability etc.).
You can access these functions using the menu. Press menu ► Probability ► Distributions ► Binomial Pdf.
In this case a dialog box will appear. Descriptions in the dialog box will help you entering the correct values.
You can use the CATALOG button, too.

Page Sorter

Page Sorter is a special program which will help you organize documents with multiple pages. It shows all pages (as icons) on the same screen and then you can select what to do with them.

Entering Page Sorter: Press ctrl ▲ (i.e. ctrl button and cursor up on the touchpad at the same time).
Deleting a page: When in the Page Sorter mode you can delete a whole page by selecting it and then pressing del.
Exiting Page Sorter: Press ctrl ▼ (i.e. ctrl button and cursor down on the touchpad at the same time). Or simply select a page and CLICK it.

Index

XMin:	-7.12345
XMax:	7.12345
XScale:	Auto
YMin:	-5.12345
YMax:	5.12345
YScale:	Auto