Trigonometry

Solving a right-angled triangle

In a right-angled triangle trigonometric functions can be used:

\(\sin\alpha=\frac{\textstyle opposite}{\textstyle hypotenuse}\)

\(\cos\alpha=\frac{\textstyle adjacent}{\textstyle hypotenuse}\)

\(\tan\alpha=\frac{\textstyle opposite}{\textstyle adjacent}\)

In a right-angled triangle \(ABC\), \(A\hat{C}B=90^\circ,~ A\hat{B}C=37^\circ\) and \(a=BC=14~\mathrm{cm}\).

(a) Find the lengths of the other two sides \(b=AC\) and \(c=AB\).

(b) Calculate the perimeter \(P\) of the triangle.

Solutions: (a) \(b\approx10.5~\mathrm{cm},~ c\approx17.5~\mathrm{cm}\); (b) \(P=a+b+c\approx42.1~\mathrm{cm}\)

In a right-angled triangle \(ABC\), \(A\hat{C}B=90^\circ,~ A\hat{B}C=30^\circ\) and \(a=BC=12~\mathrm{cm}\).

(a) Find the lengths of the other two sides \(b=AC\) and \(c=AB\).

(b) Calculate the perimeter \(P\) of the triangle.

Solutions: (a) \(b=4\sqrt{3}~\mathrm{cm}\approx6.93~\mathrm{cm}\), \(c=8\sqrt{3}~\mathrm{cm}\approx13.9~\mathrm{cm}\); (b) \(P=a+b+c=12+12\sqrt{3}~\mathrm{cm}\approx32.8~\mathrm{cm}\)

In a right-angled triangle \(ABC\), \(A\hat{C}B=90^\circ,~ B\hat{A}C=52.5^\circ\) and \(c=AB=17~\mathrm{cm}\).

(a) Find the lengths of the other two sides.

(b) Calculate the perimeter \(P\) of the triangle.

Solutions: (a) \(a\approx13.5~\mathrm{cm},~ b\approx10.3~\mathrm{cm}\); (b) \(P=a+b+c\approx40.8~\mathrm{cm}\)

In a right-angled triangle \(ABC\), \(A\hat{C}B=90^\circ,~ a=BC=15~\mathrm{cm}\) and \(b=AC=8~\mathrm{cm}\).

(a) Find the length of the hypotenuse.

(b) Calculate the angles \(\alpha=B\hat{A}C\) and \(\beta=A\hat{B}C\).

Solutions: (a) \(c=AB=17~\mathrm{cm}\); (b) \(\alpha\approx61.9^\circ,~ \beta\approx28.1^\circ\)

In a right-angled triangle \(ABC\) the hypotenuse is \(c=25~\mathrm{cm}\) and one of the catheti is \(b=7~\mathrm{cm}\).

(a) Find the perimeter of this triangle.

(b) Calculate the angles \(\alpha\) and \(\beta\).

Solutions: (a) \(a=24~\mathrm{cm},~ P=56~\mathrm{cm}\); (b) \(\alpha\approx73.7^\circ,~ \beta\approx16.3^\circ\)

In an isosceles triangle \(\triangle ABC\), \(a=b=7~\mathrm{cm}\) and \(\alpha=B\hat{A}C=68^\circ\).

(a) Find the length of the side \(c\).

(b) Find the length of the height \(h_c\).

Solutions: (a) \(c\approx5.24~\mathrm{cm}\); (b) \(h_c\approx6.49~\mathrm{cm}\)

Isosceles triangle \(\triangle ABC\) \((a=b)\) has the base \(c=AB=24~\mathrm{cm}\) and the height \(h_c=35~\mathrm{cm}\).

(a) Find the perimeter of this triangle.

(b) Calculate the angles of this triangle.

Solutions: (a) \(P=24+37+37=98~\mathrm{cm}\); (b) \(\alpha=\beta\approx71.1^\circ,~ \gamma\approx37.8^\circ\)

Rectangle \(ABCD\) has the diagonal \(e=AC=20~\mathrm{cm}\). The angle between this diagonal and the side \(a=AB\) is \(C\hat{A}B=27^\circ45'\).

(a) Find the sides of this rectangle.

(b) Calculate the acute angle between the diagonals.

Solutions: (a) \(a\approx17.7~\mathrm{cm},~ b\approx9.31~\mathrm{cm}\); (b) \(\varphi=55.5^\circ=55^\circ30'\)

Rectangle \(ABCD\) has the side \(a=AB=18~\mathrm{cm}\). The angle between the diagonal \(d=AC\) and the side \(a\) is \(C\hat{A}B=30^\circ\). Find the side \(b=BC\) and the diagonal \(d=AC\). Write your results in the exact form.
Solutions: \(b=6\sqrt{3}~\mathrm{cm},~ d=12\sqrt{3}~\mathrm{cm}\)

The diagonals of the rhombus \(ABCD\) have lengths \(e=AC=30~\mathrm{cm}\) and \(f=BD=16~\mathrm{cm}\).

(a) Find the side \(a=AB\).

(b) Calculate the angle \(\alpha=D\hat{A}B\).

Solutions: (a) \(a=17~\mathrm{cm}\); (b) \(\alpha\approx56.1^\circ\)

A regular pentagon \(ABCDE\) is inscribed in the circle with the radius \(r=10~\mathrm{cm}\). Find the side \(a=AB\) of this pentagon.
Solution: \(a\approx11.8~\mathrm{cm}\)

A regular hexagon \(ABCDEF\) has the side \(a=7~\mathrm{cm}\). Find the length of the diagonal \(d=AE\).
Solution: \(d=7\sqrt{3}~\mathrm{cm}\approx12.1~\mathrm{cm}\)

In a triangle \(\triangle ABC\), \(\alpha=C\hat{A}B=60^\circ,~ \beta=A\hat{B}C=45^\circ\) and the height \(h_c=4\sqrt{3}~\mathrm{cm}\). Find the lengths of the sides \(a,~ b\) and \(c\). Write the exact values.
Solutions: \(a=4\sqrt{6}~\mathrm{cm},~ b=8~\mathrm{cm},~ c=(4+4\sqrt{3})~\mathrm{cm}\)

Annie has a 3 m long ladder. She will place it against a vertical wall so that the bottom part of the ladder is 75 cm apart from the wall (and the top of the ladder touches the wall).

(a) Find the height to which the top of the ladder will reach.

(b) Calculate the angle between the wall and the ladder.

Solutions: (a) \(a\approx2.90~\mathrm{m}=290~\mathrm{cm}\); (b) \(\alpha\approx14.5^\circ\)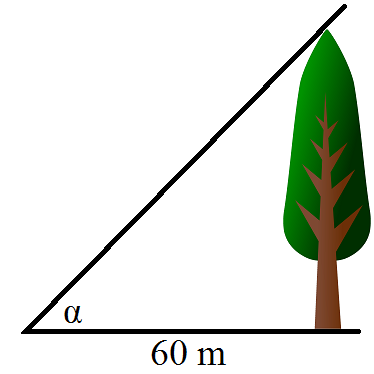

We are looking at a tree from the distance of 60 m. From a point on the ground the angle of elevation of the top of this tree is 25°. Find the height of this tree.
Solution: Height = 28 m.

Solving a general triangle

In a triangle \(ABC\), \(b=AC=6~\mathrm{cm},~ c=AB=10~\mathrm{cm}\) and \(\alpha=C\hat{A}B=70^\circ\). The height \(h_c\) has the endpoints \(C\) and \(H\).

(a) Find the height \(h_c\).

(b) Find the distances \(AH\) and \(HB\).

Solutions: (a) \(h_c\approx5.64~\mathrm{cm}\); (b) \(AH\approx2.05~\mathrm{cm},~ HB\approx7.95~\mathrm{cm}\); (c) \(a\approx9.74~\mathrm{cm}\)

The cosine rule can be used in any triangle:

\(a^2=b^2+c^2-2bc\cos\hat{A}\)

\(b^2=a^2+c^2-2ac\cos\hat{B}\)

\(c^2=a^2+b^2-2ab\cos\hat{C}\)

In a triangle \(ABC\), \(b=AC=5~\mathrm{cm},~ c=AB=8~\mathrm{cm}\) and \(\alpha=C\hat{A}B=60^\circ\). Find the length of the side \(a\).
Solution: \(a=7~\mathrm{cm}\)

In a triangle \(ABC\), \(a=BC=13~\mathrm{cm},~ b=AC=19~\mathrm{cm}\) and \(\gamma=A\hat{C}B=64^\circ30'\). Find the length of the side \(c\).
Solution: \(c\approx17.8~\mathrm{cm}\)

In a triangle \(ABC\), \(a=BC=9~\mathrm{cm},~ b=AC=14~\mathrm{cm}\) and \(c=AB=13~\mathrm{cm}\). Calculate the angles \(\alpha,\beta\) and \(\gamma\).
Solutions: \(\alpha\approx38.7^\circ,~ \beta\approx76.7^\circ,~ \gamma\approx64.6^\circ\)

In a triangle \(ABC\), \(a=BC=13~\mathrm{cm},~ b=AC=8~\mathrm{cm}\) and \(c=AB=7~\mathrm{cm}\). Calculate the angles \(\alpha,\beta\) and \(\gamma\). Write your results in degrees and minutes.
Solutions: \(\alpha=120^\circ,~ \beta\approx32^\circ12',~ \gamma\approx27^\circ48'\)

In a triangle \(\triangle ABC\), \(a=BC=2~\mathrm{cm},~ b=AC=7~\mathrm{cm}\) and \(c=AB=3\sqrt{3}~\mathrm{cm}\). Calculate the angle \(\beta\).
Solution: \(\beta=150^\circ\)

In a triangle \(\triangle ABC\), \(a=23~\mathrm{cm},~ c=17~\mathrm{cm}\) and \(\beta=107^\circ\).

(a) Find the side \(b\).

(b) Calculate the angles \(\alpha\) and \(\gamma\).

Solutions: (a) \(b\approx32.4~\mathrm{cm}\); (b) \(\alpha\approx42.8^\circ,~ \gamma\approx30.2^\circ\)

In a triangle \(\triangle ABC\), \(\alpha=30^\circ,~ \beta=71^\circ\) and \(b=16~\mathrm{cm}\).

(a) Find the height \(h_c\).

(b) Calculate the side \(a\).

Solutions: (a) \(h_c=8~\mathrm{cm}\); (b) \(a\approx8.46~\mathrm{cm}\)

The sine rule can be used in any triangle:

\(\frac{\textstyle a}{\textstyle \sin\hat{A}}=\frac{\textstyle b}{\textstyle \sin\hat{B}}=\frac{\textstyle c}{\textstyle \sin\hat{C}}\)

In a triangle \(\triangle ABC\), \(\alpha=57^\circ,~ \beta=71^\circ\) and \(c=15~\mathrm{cm}\).

(a) Find the angle \(\gamma\).

(b) Find the sides \(a\) and \(b\).

Solutions: (a) \(\gamma=52^\circ\); (b) \(a\approx16.0~\mathrm{cm},~ b\approx18.0~\mathrm{cm}\)

In a triangle \(\triangle ABC\), \(a=23~\mathrm{cm},~ b=39~\mathrm{cm}\) and \(\beta=83^\circ\).

(a) Find the angles \(\alpha\) and \(\gamma\).

(b) Find the side \(c\).

Solutions: (a) \(\alpha\approx35.8^\circ,~ \gamma\approx61.2^\circ\); (b) \(c\approx34.4~\mathrm{cm}\)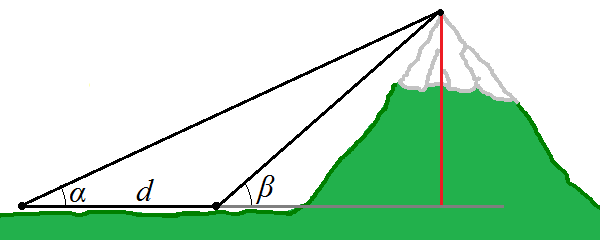

We watch the peak of a mountain from two different points in the plain. When viewed from the first point, the angle of elevation of the peak is \(\alpha=35^\circ\). When viewed from the second point, the angle of elevation of the peak is \(\beta=50^\circ\). The distance between the two points is \(d=430~\mathrm{m}\). Calculate the height of this mountain above the plain.
Height of a mountain

Solutions: \(h\approx730~\mathrm{m}\)

Area

Area of a triangle can be calculated using the formula:

\(A=\frac{\textstyle base\times height}{\textstyle 2}\)

or also using:

\(A=\frac{1}{2}\,ab\sin\hat{C}\)

\(A=\frac{1}{2}\,ac\sin\hat{B}\)

\(A=\frac{1}{2}\,bc\sin\hat{A}\)

In a triangle \(\triangle ABC\), \(b=6~\mathrm{cm},~ c=8~\mathrm{cm}\) and \(\alpha=30^\circ\).

(a) Find the height \(h_c\).

(b) Find the area \(A\).

Solutions: (a) \(h_c=3~\mathrm{cm}\); (b) \(A=12~\mathrm{cm}^2\)

In a triangle \(\triangle ABC\), \(a=14~\mathrm{cm},~ c=11~\mathrm{cm}\) and \(\beta=77^\circ33'\).

(a) Find the side \(b\).

(b) Find the area \(A\).

Solutions: (a) \(b\approx15.8~\mathrm{cm}\); (b) \(A\approx75.2~\mathrm{cm}^2\)

In a triangle \(\triangle ABC\), \(a=5~\mathrm{cm},~ b=2~\mathrm{cm}\) and \(\gamma=58^\circ\). Find the area of this triangle.
Solution: \(A\approx4.24~\mathrm{cm}^2\)

In a triangle \(\triangle ABC\), \(a=7~\mathrm{cm},~ b=8~\mathrm{cm}\) and \(c=5~\mathrm{cm}\).

(a) Find the angle \(\alpha=C\hat{A}B\).

(b) Find the area \(A\).

Solutions: (a) \(\alpha=60^\circ\); (b) \(A=10\sqrt{3}~\mathrm{cm}\approx17.3~\mathrm{cm}^2\)

Area of a triangle can be calculated using the Heron formula if you know all three sides:

\(A=\sqrt{s(s-a)(s-b)(s-c)}\)

where \(s=\frac{\textstyle a+b+c}{\textstyle 2}\)

A triangle \(\triangle ABC\) has sides: \(a=26~\mathrm{cm},~ b=15~\mathrm{cm}\) and \(c=37~\mathrm{cm}\). Find the area of this triangle.
Solution: \(A=156~\mathrm{cm}^2\)

A triangle \(\triangle ABC\) has sides: \(a=14~\mathrm{cm},~ b=19~\mathrm{cm}\) and \(c=7~\mathrm{cm}\). Find the area of this triangle.
Solution: \(A\approx39.5~\mathrm{cm}^2\)

A triangle \(\triangle ABC\) has sides: \(a=6~\mathrm{cm},~ b=8~\mathrm{cm}\) and \(c=17~\mathrm{cm}\). Find the area of this triangle.
Solution: A triangle with these sides doesn't exist.

A triangle \(\triangle ABC\) has the sides: \(a=17~\mathrm{cm},~ b=10~\mathrm{cm}\) and \(c=21~\mathrm{cm}\).

(a) Find the area.

(b) Find the height \(h_c\).

Solutions: (a) \(A=84~\mathrm{cm}^2\); (b) \(h_c=8~\mathrm{cm}\)

In a triangle \(\triangle ABC\): \(\alpha=39^\circ,~ \beta=68^\circ\) and \(c=14~\mathrm{cm}\).

(a) Find the angle \(\gamma\).

(b) Find the sides \(a\) and \(b\).

Solutions: (a) \(\gamma=73^\circ\); (b) \(a\approx9.21~\mathrm{cm},~ b\approx13.6~\mathrm{cm}\); (c) \(P\approx36.8~\mathrm{cm},~ A\approx59.8~\mathrm{cm}^2\)

In a parallelogram \(ABCD\): \(a=AB=15~\mathrm{cm},~ b=BC=7~\mathrm{cm}\) and \(\alpha=B\hat{A}D=60^\circ\).

(a) Find the diagonal \(f=BD\).

(b) Find the area of this parallelogram.

Solutions: (a) \(f=13~\mathrm{cm}\); (b) \(A\approx90.9~\mathrm{cm}^2\)

A rhombus \(ABCD\) has the side \(a=7~\mathrm{cm}\) and the angle \(\alpha=69^\circ\).

(a) Find the diagonal \(f=BD\).

(b) Find the height \(h\).

Solutions: (a) \(f\approx7.93~\mathrm{cm}\); (b) \(h\approx6.54~\mathrm{cm}\); (c) \(A\approx45.7~\mathrm{cm}^2\)

Farmer has a field in form of a quadrilateral \(ABCD\). He measured the sides: \(AB=140~\mathrm{m}\), \(BC=85~\mathrm{m}\), \(CD=125~\mathrm{m}\), \(DA=80~\mathrm{m}\). Finally, he measured one of the diagonals: \(AC=195~\mathrm{m}\). Determine the area of this field.
Solution: \(A\approx 8250~\mathrm{m}^2\)

A regular pentagon is inscribed in the circle with the radius \(r=8~\mathrm{cm}\).

(a) Find the side of this pentagon.

(b) Find the diagonal.

Solutions: (a) \(a\approx9.40~\mathrm{cm}\); (b) \(d\approx15.2~\mathrm{cm}\); (c) \(A\approx152~\mathrm{cm}^2\)

A regular octagon \(ABCDEFGH\) has the side \(a=10~\mathrm{cm}\).

(a) Find the diagonal \(AC\).

(b) Find the inradius \(r\) (radius of the inscribed circle).

Solutions: (a) \(AC\approx18.5~\mathrm{cm}\); (b) \(r\approx12.1~\mathrm{cm}\); (c) \(A\approx483~\mathrm{cm}^2\)

A regular nonagon has the side \(a=6~\mathrm{cm}\).

(a) Find the circumradius \(R\) (radius of the circumscribed circle).

(b) Find the length of the longest diagonal.

Solutions: (a) \(R\approx8.77~\mathrm{cm}\); (b) \(d\approx17.3~\mathrm{cm}\); (c) \(A\approx223~\mathrm{cm}^2\)

A regular hexagon has the side \(a=16~\mathrm{cm}\).

(a) Find the area of this hexagon.

(b) Find the circumradius \(R\) (radius of the circumscribed circle).

(d) By what percentage is the circumradius greater than the inradius?

Solutions: (a) \(A\approx665~\mathrm{cm}^2\); (b) \(R=a=16~\mathrm{cm}\); (c) \(r\approx13.9~\mathrm{cm}\); (d) By \(15.5\%\)

Circle, arc, circular sector and circular segment

A circle has the radius \(r=5~\mathrm{cm}\). Find the area and perimeter of this circle.
Solutions: \(A=25\pi~\mathrm{cm}^2\approx78.5~\mathrm{cm}^2,~ P=10\pi~\mathrm{cm}\approx31.4~\mathrm{cm}\)

A circle has the circumference \(100~\mathrm{cm}\). Find the area of this circle.
Solutions: \(r\approx15.9~\mathrm{cm},~ A\approx796~\mathrm{cm}^2\)

A circle has the area \(A=95~\mathrm{cm}^2\). Calculate the radius and the perimeter of this circle.
Solutions: \(r\approx5.50~\mathrm{cm},~ P\approx34.6~\mathrm{cm}\)

A circle has the radius \(r=10~\mathrm{cm}\),

(a) Find the circumference.

(b) Find the length of the arc with the central angle \(90^\circ\).

(d) Find the area of the circular sector with the central angle \(90^\circ\).

Solutions: (a) \(P\approx62.8~\mathrm{cm}\); (b) \(L\approx15.7~\mathrm{cm}\); (c) \(A_0\approx314~\mathrm{cm}^2\); (d) \(A_1\approx78.5~\mathrm{cm}^2\)

Length of an arc can be calculated using the formula:

\(L=2\,\pi\,r\,\frac{\textstyle \theta}{\textstyle 360^\circ}\) or

\(L=\pi\,r\,\frac{\textstyle \theta}{\textstyle 180^\circ}\)

Area of a circular sector can be calculated using the formula:

\(A=\pi\,r^2\,\frac{\textstyle \theta}{\textstyle 360^\circ}\)

A circle has the radius \(r=12~\mathrm{cm}\). Find the length of the arc with the central angle \(\theta=40^\circ\).
Solution: \(L=\frac{8}{3}\pi~\mathrm{cm}\approx8.38~\mathrm{cm}\)

Find the area of the sector of the circle with the radius \(r=18~\mathrm{cm}\) and the central angle \(\theta=10^\circ\).
Solution: \(A=9\pi~\mathrm{cm}^2\approx28.3~\mathrm{cm}^2\)

In a circle with the radius \(r=15~\mathrm{cm}\), arc \(L\) subtends the angle \(69^\circ\) at the centre.

(a) Find the length of the arc \(L\).

(b) Find the area of the corresponding circular sector.

Solutions: (a) \(L\approx18.1~\mathrm{cm}\); (b) \(A\approx135~\mathrm{cm}^2\)

A circular sector has the radius \(r=18~\mathrm{cm}\). The area of this sector is \(A=288~\mathrm{cm}^2\).

(a) Find the corresponding central angle.

(b) Find the length of the corresponding circular arc.

Solutions: (a) \(\theta\approx102^\circ\); (b) \(L=32~\mathrm{cm}\)

Given the radius \(r=8~\mathrm{cm}\) and central angle \(\theta=90^\circ\),

(a) find the area of the circular sector,

(b) find the area of the corresponding circular segment.

Solutions: (a) \(A_1\approx50.3~\mathrm{cm}^2\); (b) \(A_2\approx18.3~\mathrm{cm}^2\)

A circle has the radius \(r=26~\mathrm{cm}\). Calculate the area of the circular segment corresponding to the central angle \(\theta=125^\circ\).
Solution: \(A\approx461~\mathrm{cm}^2\)

Circular segment is a part of the circle with \(r=13~\mathrm{cm}\). The arc corresponding to this circular segment has the length \(L=15~\mathrm{cm}\). Calculate the area of this circular segment.
Solution: \(A\approx20.2~\mathrm{cm}^2\)

Measuring angles in radians

Write the following angles in radians:

(a) \(30^\circ\)

(b) \(45^\circ\)

(d) \(135^\circ\)

Solutions: (a) \(30^\circ=\frac{\pi}{6}\); (b) \(45^\circ=\frac{\pi}{4}\); (c) \(120^\circ=\frac{2\pi}{3}\); (d) \(135^\circ=\frac{3\pi}{4}\)

Convert the following angles to radians. Round the results to three significant figures.

(a) \(75^\circ\)

(b) \(20^\circ\)

(d) \(1^\circ\)

Solutions: (a) \(75^\circ=\frac{5\pi}{12}\approx1.31\); (b) \(20^\circ=\frac{\pi}{9}\approx0.349\); (c) \(10^\circ=\frac{\pi}{18}\approx0.175\); (d) \(1^\circ=\frac{\pi}{180}\approx0.0175\)

Convert the following angles to degrees:

(a) \(\frac{\pi}{3}\)

(b) \(\frac{\pi}{2}\)

(d) \(\frac{5\pi}{4}\)

Solutions: (a) \(\frac{\pi}{3}=60^\circ\); (b) \(\frac{\pi}{2}=90^\circ\); (c) \(\frac{5\pi}{6}=150^\circ\); (d) \(\frac{5\pi}{4}=225^\circ\)

Convert the following angles to degrees:

(a) \(1\)

(b) \(0.25\)

(d) \(3.14\)

Solutions: (a) \(1~\mathrm{rad}\approx57.3^\circ\); (b) \(0.25~\mathrm{rad}\approx14.3^\circ\); (c) \(1.85~\mathrm{rad}\approx106^\circ\); (d) \(3.14~\mathrm{rad}\approx180^\circ\)

A circle has the radius \(r=9~\mathrm{cm}\). Find the length of the arc which subtends the angle \(\theta=2~\mathrm{radians}\).
Solution: \(L=18~\mathrm{cm}\)

Given the radius \(r=6~\mathrm{cm}\) and central angle \(\theta=\frac{1}{8}\pi\),

(a) find the area of the circular sector,

(b) find the length of the arc.

Solutions: (a) \(A\approx7.07~\mathrm{cm}^2\); (b) \(L\approx2.36~\mathrm{cm}\)

Find the area of the circular segment of the radius \(r=14~\mathrm{cm}\) and central angle \(\theta=1\).
Solution: \(A\approx15.5~\mathrm{cm}^2\)