Trigonometric functions

Trigonometric functions

Graphs of trig functions in degrees

In all exercises in this section we'll be using degrees as angular units. To draw graphs correctly you must set the angular unit setting to "Degrees". Besides, you must fix the values in window settings: Xmin = −360, Xmax = 360 (and Xscale = 90 might be a good idea, too).

Draw the graph of the function \(f(x)=\sin x\) and determine the following properties:

(a)   find the minimum value and the maximum value,

(b)   find the period.
Solutions:    (a)  min. value: \(-1\), max. value: \(1\);     (b)  period: \(360^\circ\)
Draw the graph of the function \(f(x)=2\sin x\) and determine the following properties:

(a)   find the minimum value and the maximum value,

(b)   find the period.
Solutions:    (a)  min. value: \(-2\), max. value: \(2\);     (b)  period: \(360^\circ\)
?

?
Coefficients in the equation   \(y=A\,\sin x+D\)   have the meaning:

\(A=\) amplitude,   \(D=\) vertical shift

Principal axis has the equation: \(y=D\).
Draw the graph of the function \(f(x)=2\sin x+1\) and determine the following properties:

(a)   find the amplitude,

(b)   find the principal axis,

(c)   find the minimum value and the maximum value,

(d)   find the period.
Solutions:    (a)  amplitude: \(2\);     (b)  principal axis: \(y=1\);     (c)  min. value: \(-1\), max. value: \(3\);     (d)  period: \(360^\circ\)
?

?
Coefficient in the equation   \(y=\sin Bx\)   has the meaning:

\(B=\) horizontal shrink

Period of the function is \(\frac{360^\circ}{B}\).
Draw the graph of the function \(f(x)=\sin 3x\) and determine the following properties:

(a)   find the minimum value and the maximum value,

(b)   find the period.
Solutions:    (a)  min. value: \(-1\), max. value: \(1\);     (b)  period: \(120^\circ\)
?

?
Coefficient in the equation   \(y=\sin (x-C)\)   has the meaning:

\(C=\) horizontal shift
Draw the graph of the function \(f(x)=\sin (x-45^\circ)\) and determine the following properties:

(a)   find the minimum value and the maximum value,

(b)   find the period.
Solutions:    (a)  min. value: \(-1\), max. value: \(1\);     (b)  period: \(360^\circ\)
Draw the graph of the function \(f(x)=\sin 2(x-20^\circ)\) and determine the following properties:

(a)   find the minimum value and the maximum value,

(b)   find the period.
Solutions:    (a)  min. value: \(-1\), max. value: \(1\);     (b)  period: \(180^\circ\)
Draw the graph of the function \(f(x)=\cos x\) and determine the following properties:

(a)   find the minimum value and the maximum value,

(b)   find the period.
Solutions:    (a)  min. value: \(-1\), max. value: \(1\);     (b)  period: \(360^\circ\)
Draw the graph of the function \(f(x)=3\cos x+1\) and determine the following properties:

(a)   find the principal axis,

(b)   write down the range,

(c)   find all minima for \(0^\circ\leqslant x\leqslant 360^\circ\).
Solutions:    (a)  principal axis: \(y=1\);     (b)  range: \(-2\leqslant y \leqslant 4\);     (c)  minimum at: \((180^\circ,-2)\)
Draw the graph of the function \(f(x)=\cos3x\) and determine the following properties:

(a)   find all \(x\)-intercepts for \(0^\circ\leqslant x\leqslant 360^\circ\),

(b)   write down minima and maxima for \(0^\circ\leqslant x\leqslant 360^\circ\).
Solutions:    (a)  \(x\)-intercepts: \(30^\circ,~90^\circ,~150^\circ,~210^\circ,~270^\circ,~330^\circ\);     (b)  min.: \((60^\circ,-1),~(180^\circ,-1),~(300^\circ,-1)\), max.:\((0^\circ,1),~(120^\circ,1),~(240^\circ,1),~(360^\circ,1)\)
Draw the graph of the function \(f(x)=4\cos\left(x-30^\circ\right)\) and determine the following properties:

(a)   find \(y\)-intercept,

(b)   find all \(x\)-intercepts on \([0,360^\circ]\),

(c)   write down the greatest and the least value, and state the smallest non-negative value of \(x\) for which they occur.
Solutions:    (a)  \(y\)-intercept: \(2\sqrt{3}\);     (b)  \(x\)-intercepts: \(120^\circ,~ 300^\circ\);     (c)  min. value \(-4\) occurs at \(x=210^\circ\), max. value \(4\) occurs at \(x=30^\circ\)
Graph of a function \(y=f(x)\) is drawn in the picture below.

(a)   find the principal axis, amplitude and period,

(b)   write the function in the form \(y=A\sin x +D\)

Solutions:    (a)  principal axis: \(y=3\), amplitude: \(2\), period \(360^\circ\);     (b)  \(y=2\sin x+3\)
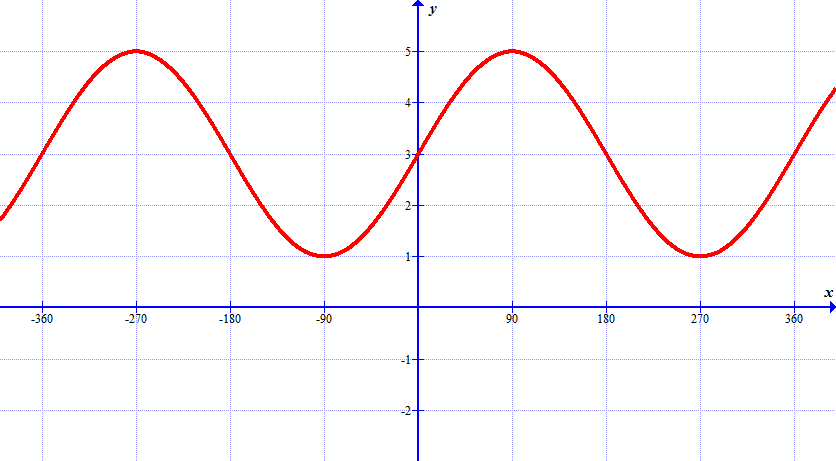
Graph of a function \(y=f(x)\) is drawn in the picture below.

(a)   find the principal axis, amplitude and period,

(b)   write the function in the form \(y=A\sin Bx +D\)

Solutions:    (a)  principal axis: \(y=2\), amplitude: \(3\), period \(180^\circ\);     (b)  \(y=3\sin 2x+2\)
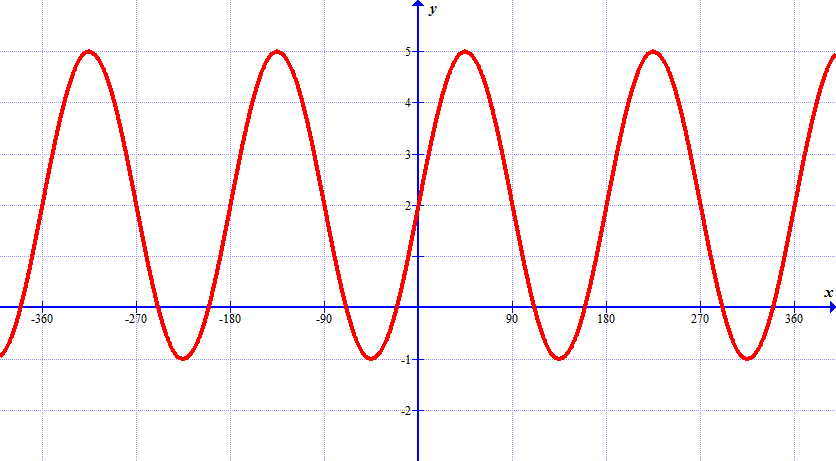
Use your GDC to draw the graph of the function \(f(x)=\sin x+\sqrt{3}\cos x\). This function can be written in the form \(f(x)= A\sin(x+C)\). Find the values of the constants \(A\) and \(C\).
Solutions: \(A=2,~ C=60^\circ\); \(f(x)=2\sin(x+60^\circ)\)
Use your GDC to draw the graph of the function \(f(x)=\sin^2 x\). Then write this function in the form \(f(x)= A\cos Bx+D\).
Solutions: \(f(x)=-\frac{1}{2}\cos 2x+\frac{1}{2}\) (Use the GDC to verify your solution.)

Graphs of trig functions in radians

In all exercises in this section we'll be using radians as angular units. To draw graphs correctly you must set the angular unit setting to "Radians". Besides, you must fix the values in window settings: Xmin = −6.283 , Xmax = 6.283 (and Xscale = 1.571 might be a good idea, too).

Draw the graph of the function \(f(x)=\sin x\) and determine the following properties:

(a)   find the minimum value and the maximum value,

(b)   find the period.
Solutions:    (a)  min. value: \(-1\), max. value: \(1\);     (b)  period: \(2\pi\) radians
Draw the graph of the function \(f(x)=\cos x\) and determine the following properties:

(a)   find the minimum value and the maximum value,

(b)   find the period.
Solutions:    (a)  min. value: \(-1\), max. value: \(1\);     (b)  period: \(2\pi\) radians
Draw the graph of the function \(f(x)=2\cos x+1\) and determine the following properties:

(a)   find the principal axis,

(b)   find the minimum value and the maximum value,

(c)   find the period.
Solutions:    (a)  principal axis: \(y=1\);     (b)  min. value: \(-1\), max. value: \(3\);     (c)  period: \(2\pi\)
Draw the graph of the function \(f(x)=\sin2x+3\) and determine the following properties:

(a)   find the domain and range,

(b)   find the period,

(c)   write down minima and maxima.
Solutions:    (a)  domain: \(\mathbb{R}\), range: \([2,4]\);     (b)  period: \(\pi\);     (c)  min.: \((-\frac{\pi}{4}+k\pi,2)\), max.:\((\frac{\pi}{4}+k\pi,4),~~ k\in\mathbb{Z}\)
Draw the graph of the function \(f(x)=\cos3x\) and determine the following properties:

(a)   find all \(x\)-intercepts on \(0\leqslant x\leqslant 2\pi\),

(b)   write down minima and maxima on \(0\leqslant x\leqslant 2\pi\).
Solutions:    (a)  \(x\)-intercepts: \(\frac{\pi}{6},~\frac{\pi}{2},~\frac{5\pi}{6},~\frac{7\pi}{6},~\frac{3\pi}{2},~\frac{11\pi}{6}\);     (b)  min.: \((\frac{\pi}{3},-1),~(\pi,-1),~(\frac{5\pi}{3},-1)\), max.:\((0,1),~(\frac{2\pi}{3},1),~(\frac{4\pi}{3},1),~(2\pi,1)\)
Draw the graph of the function \(f(x)=4\cos\left(x-\frac{\pi}{6}\right)\) and determine the following properties:

(a)   find \(y\)-intercept,

(b)   find all \(x\)-intercepts on \([0,2\pi]\),

(c)   write down the greatest and the least value, and state the smallest non-negative value of \(x\) for which they occur.
Solutions:    (a)  \(y\)-intercept: \(2\sqrt{3}\);     (b)  \(x\)-intercepts: \(\frac{2\pi}{3},~ \frac{5\pi}{3}\);     (c)  min. value \(-4\) occurs at \(x=\frac{7\pi}{6}\), max. value \(4\) occurs at \(x=\frac{\pi}{6}\)

Index