Straight lines have the equations \(y=2x-3\) and \(y=-\frac{2}{3}x+5\).
(a) Draw these two straight lines.
(b) Find the intersection point.
These two straight lines together with the axis of abscissas form a triangle \(ABC\).
(c) Calculate the area of this triangle.
(d) Calculate the perimeter of this triangle.
(e) Is this a right-angled triangle? Justify your answer.
Solutions :
(b) \(P(3,3)\);
(c) \(A=9\);
(d) \(P\approx14.8\);
(e) No, it isn't, because …
Consider the function \(f(x)=x+|2x-3|\). The graph of \(f\) and straight line \(x-2y+9=0\)
enclose a triangular region.
(a) Find all three vertices of this triangle.
(b) Find the area of this triangle.
Solutions :
(a) \(A(1.5,1.5),~ B(-1,4),~ C(3,6)\);
(b) \(A=\frac{15}{2}=7.5\)
Function \(f\) has the equation:
\(f(x)=2x^2-10x+8\).
(a) Draw the graph of this function.
(b) Write the function in the form \(f(x)=a(x-p)(x-q)\).
(c) Find the vertex of \(f\).
Draw the function \(g(x)=2x-8\) in the same coordinate system.
(d) Find the coordinates of the intersection points.
(e) Calculate the area enclosed by \(f\) and \(g\).
Solutions :
(b) \(f(x)=2(x-1)(x-4)\);
(c) \(V(2.5,-4.5)\);
(d) \(P_1(2,-4),~P_2(4,0)\);
(e) \(A=\frac{8}{3}\approx2.67\)
Function \(f\) is a quadratic function. It intercepts the \(x\)-axis at 1 and 4. The \(y\)-axis intercept
has coordinates \(P(0, -4)\).
(a) Write the equation of \(f\):
(i) in the form: \(f(x)=a(x-p)(x-q)\)
(ii) in the form: \(f(x)=ax^2+bx+c\)
(b) Draw the graph of \(f\).
Graph of \(f\) passes through points \(A(2,m)\) and \(B(5,n)\).
(c) Find \(m\) and \(n\).
Straight line \(L\) passes through \(A\) and \(B\), too.
(d) Write the equation of \(L\).
(e) Calculate the area enclosed by \(f\) and \(L\).
Solutions :
(a) \(f(x)=-(x-1)(x-4),~~f(x)=-x^2+5x-4\);
(c) \(m=2,~ n=-4\);
(d) \(y=-2x+6\);
(e) \(A=\frac{9}{2}=4.5\)
Function \(f\) has the equation \(f(x)=x^3+x^2-x+2\).
(a) Draw the graph of \(f\).
(b) Find \(x\)- and \(y\)-axis intercepts.
(c) Use the derivative to find extremes of \(f\). Write the exact coordinates of extremes.
Graph of \(f\) has a tangent \(t\) at point \(P(1,f(1))\).
(d) Write the equation of \(t\).
Function \(f\) and line \(t\) have another point in common, besides \(P\). We'll label this point \(R\).
(e) Write the coordinates of \(R\).
Solutions :
(b) \((-2,0)\) and \((0,2)\);
(c) max: \((-1,3)\), min: \((\frac{1}{3},\frac{49}{27})\);
(d) tangent: \(y=4x-1\);
(e) \(R(-3,-13)\)
Graph of the function \(f(x)=x^3+ax^2+bx+c\) passes through points \(A(1,7)\), \(B(2,4)\) and \(C(3,3)\).
(a) Find \(a\), \(b\) and \(c\).
(b) Draw the graph of \(f\).
(c) Write the equation of the tangent to \(f\) at point \(C\).
(d) Find the area of the region between the graph of \(f\) and this tangent.
Solutions :
(a) \(a=-5,~ b=5,~ c=6\);
(c) \(y=2x-3\);
(d) \(A=\frac{64}{3}=21\frac{1}{3}\approx21.3\)
Let \(f(x)=\frac{1}{9}x^3-x^2+2x\).
(a) Draw the graph of \(f\).
Straight line \(L_1\) is the tangent to \(f\) at \(x=0\).
Straight line \(L_2\) is the tangent to \(f\) at \(x=3\).
(b) Write down the equation of \(L_1\).
(c) Write down the equation of \(L_2\).
(d) Find the coordinates of the intersection point of \(L_1\) and \(L_2\).
(e) Function \(f\) and lines \(L_1\) and \(L_2\) enclose a region (for \(0\leqslant x\leqslant 3\)) .
(i) Write down the expression for the area of this region.
(ii) Calculate the area of this region.
Solutions :
(b) \(L_1\!:~ y=2x\);
(c) \(L_2\!:~ y=-x+3\);
(d) \(P(1,2)\);
(e) area\(~=0.75\)
Consider the functions \(f(x)=x^3-5x^2+7x\) and \(g(x)=2x\).
(a) Write down the coordinates of all intersection points of \(f\) and \(g\).
(b) Region \(R\) is enclosed by the graph of \(f\), the horizontal axis and the vertical line \(x=m\) (for \(m\gt 0\)).
(i) Write down the area of \(R\) using a definite integral.
(ii) Write down the area of \(R\) in terms of \(m\).
(iii) Find the value of \(m\), where the area of \(R\) is 7.
Solutions :
(a) \(A(0,0),~ B(1.38,2.76),~ C(3.62,7.24)\);
(b)(i) \(A=\int\limits_0^m f(x)~dx\);
(ii) \(A=\frac{1}{4}m^4-\frac{5}{3}m^3+\frac{7}{2}m^2\);
(iii) \(m\approx3.08\)
Consider the functions \(f(x)=\sqrt{2x+12}\) and \(g(x)=x^2\).
(a) Find the domain and range of the function \(f\).
(b) Draw graphs of \(f\) and \(g\). Shade the region enclosed by these two graphs.
(c) Write the coordinates of both intersection points.
(d) Find the area of the shaded region giving your answer rounded to three significant figures.
Solutions :
(a) Domain: \(x\geqslant -6\), range: \(y\geqslant 0\);
(c) \(A(-1.71,2.93),~ B(2,4)\);
(d) \(A\approx8.62\)
Consider the function \(f(x)={\displaystyle \frac{x-4}{x-3}}\).
(a) (i) Draw the graph of \(f\).
(ii) Write down the equations of its asymptotes.
Line \(L_1\) is the tangent to \(f\) at \(x=1\) and line \(L_2\) is the tangent to \(f\) at \(x=4\) .
(b) Write equations of \(L_1\) and \(L_2\).
(c) Find the intersection point of \(L_1\) and \(L_2\).
(d) Find the area of the triangle formed by \(L_2\) and both coordinate axes.
Solutions :
(a) asymptotes: \(x=3\) and \(y=1\);
(b) \(L_1\!\!:~y=\frac{1}{4}x+\frac{5}{4}\), \(L_2\!\!:~y=x-4\);
(c) \(P(7,3)\);
(d) \(A=8\)
Function \(f\) has the equation \(f(x)={\displaystyle \frac{x+3}{x+1}}\).
(a) (i) Draw the graph of \(f\).
(ii) Write down the domain and range.
(b) Function \(f\) can be written in the form: \(f(x)={\displaystyle p + \frac{q}{x+1}}\). Find \(p\) and \(q\).
(c) Calculate the area between the graf of \(f\) and \(x\)-axis
on the interval \(0\leqslant x\leqslant 3\).
Solutions :
(a) Domain: \(x\ne -1\), range: \(y\ne 1\);
(b) \(p=1,~ q=2\);
(c) \(A\approx 5.77\)
Function \(f\) has the equation \(f(x)={\displaystyle \frac{x-1}{x-2}}\).
(a) Write the equation of the inverse function \(f^{-1}\).
(b) Graph of \(f\) has a tangent \(t\) at \(x=3\). Write
the equation of this tangent.
Straight line \(L\) is parallel to the tangent \(t\) and it passes through the point \(P(0,7.25)\).
(c) Write the equation of the line \(L\).
(d) Find the intersection points of \(f\) and \(L\).
(e) Calculate the area of the region bounded by \(f\) and \(L\).
Solutions :
(a) \(f^{-1}(x)=\frac{2x-1}{x-1}\);
(b) tangent: \(y=-x+5\);
(c) line \(L\!:~ y=-x+7.25\);
(d) \(A(2.25,5),~ B(6,1.25)\);
(e) area \(\approx5.20\)
Function \(f\) has the equation \(f(x)=\ln(x+e)\).
(a) Draw the graph of \(f\).
(b) Find the domain of \(f\).
Function \(g\) has the equation \(g(x)=e^x\).
(c) Write the equation of the normal to \(g\) at point \(A(0,1)\).
(d) Graphs of \(f\) and \(g\) have two intersection points: \(A(0,1)\) and \(B(p,q)\).
(i) Write \(p\) and \(q\) rounded to three significant figures.
(ii) Calculate the area of the region enclosed by \(f\) and \(g\).
Solutions :
(b) Domain: \(x\gt -e\);
(c) normal: \(y=-x+1\);
(d) \(p\approx-1.46,~ q\approx0.233\);
area \(\approx0.201\)
Consider the function \(f(x)=x \ln x - x\).
(a) Draw the graph of \(f\).
(b) Write the equation of the tangent to \(f\) at \(x=e\).
(c) Write the coordinates of the minimum.
Solutions :
(b) tangent: \(y=x-e\);
(c) min.: \((1,-1)\)
Consider the function \(f(x)={\displaystyle \ln\frac{1+x}{1-x}}\).
(a) Draw the graph of \(f\).
(b) Write down the domain of \(f\).
(c) Write the equation of the tangent to \(f\) at \(x=0\).
(d) Find the equation of \(f^{-1}\).
Solutions :
(b) Domain: \(-1\lt x\lt 1\);
(c) tangent: \(y=2x\);
(d) \(f^{-1}(x)=\frac{e^x-1}{e^x+1}\)
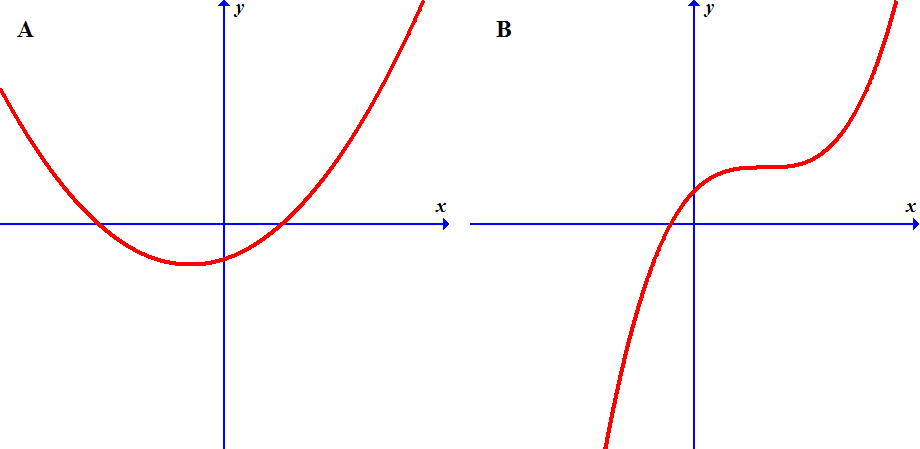
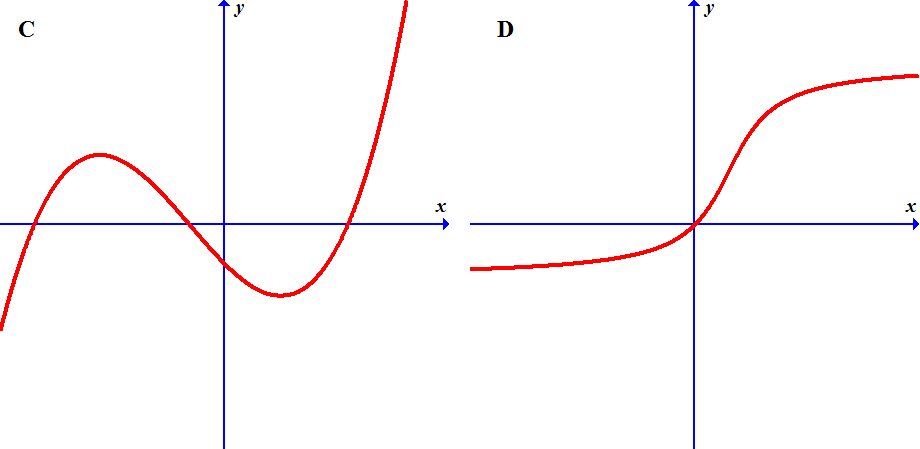
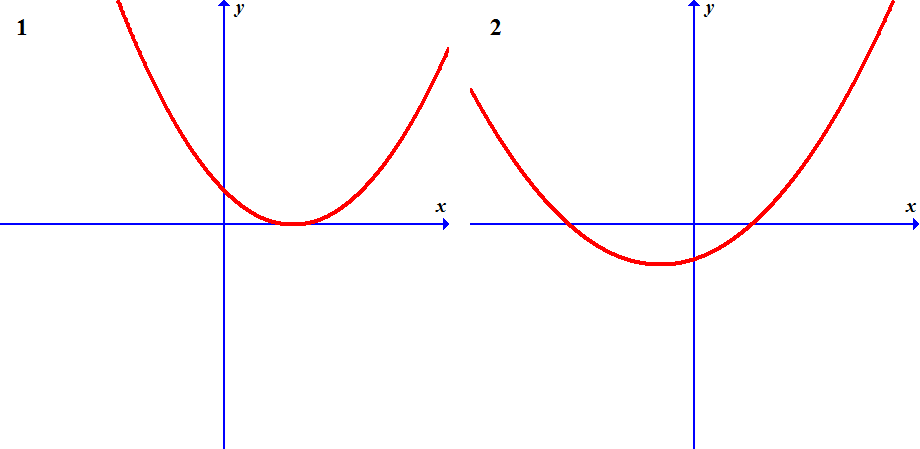
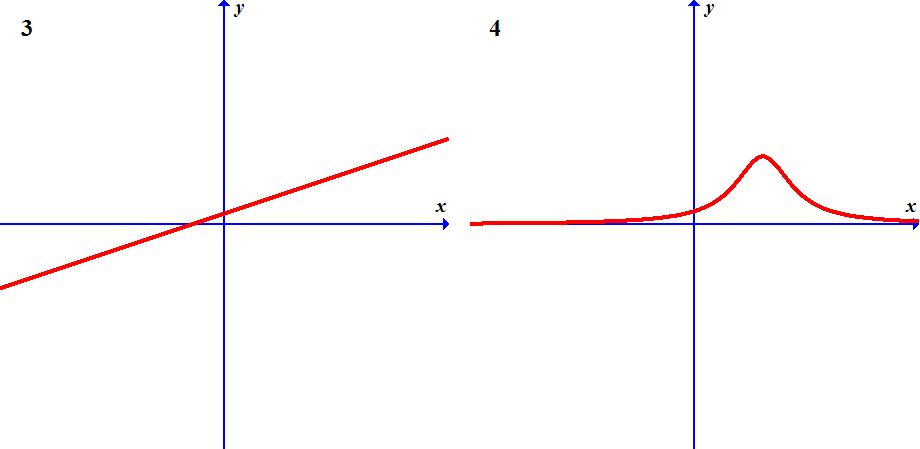
Pictures A, B, C and D show graphs of four functions.
Pictures 1, 2, 3 and 4 show graphs of their derivatives, but they are not given in the same order.
Which derivative corresponds to which function? Find the matching pairs.
Solutions :
A3 B1 C2 D4
Eduardo is building a large garden next to his house. The garden will have the form of a quadrilateral.
Two sides of this garden are two perpendicular walls. He bought
53 m of fence for the other two sides. A part of the fence \((x)\) will be parallel to one of the walls,
the other part of the fence \((y)\) will form an angle of 45° with the wall – see the diagram
(diagram is not to scale).
fence
wall
wall
x
y
GARDEN
Eduardo would like to maximize the area of the garden formed this way.
(a) Express the area of the garden as a function of the unknown \(x\) and draw the graph.
(b) (i) Find the length of \(x\) where the area is maximal.
(ii) Find the corresponding
length of the other part of the fence \((y)\).
(iii) Write down the corresponding area.
Solutions :
(Hint: You don't have to simplify the function. Just type it into your GDC. )
(b) \(x\approx12.0~\mathrm{m},~ y\approx41.0~\mathrm{m},~ A\approx768~\mathrm{m}^2\)