-
In astronomy, apparent magnitude is a measure of the brightness of a star. It's calculated from the flux density of the light coming from this star.
The formula for apparent magnitude (\(m)\) is:
\(m=-\sqrt[{\scriptstyle 5}]{100}~\log\displaystyle\frac{j}{j_0}\)
Here \(j\) is the measured flux density in watts to square meter: \(\mathrm{W/m}^2\).
The constant \(j_0=2.518\cdot10^{-8}~\mathrm{W/m}^2\) is the given reference value.
(a)Calculate the apparent magnitude of the following stars:
(i)Polaris (\(\alpha\,\)UMi) which has \(j=4.02\cdot10^{-9}~\mathrm{W/m}^2\)
(ii)Mu Cephei (\(\mu\,\)Cep) which has \(j=6.44\cdot10^{-10}~\mathrm{W/m}^2\)
(iii)Spica (\(\alpha\,\)Vir) which has \(j=10^{-8}~\mathrm{W/m}^2\)
(b)Star 47 Ursae Maioris (\(47\,\)UMi) has the apparent magnitude 5. Calculate flux density of its light.
Solutions:
(a) Polaris has \(m=2\), Mu Cephei has \(m=4\), Spica has \(m=1\);
(b) \(j=2.57\cdot10^{-10}~\mathrm{W/m}^2\)
-
The general term of an arithmetic sequence is given by: \(u_n=7n+3\).
(a)Write down the common difference.
(b)(i)Given that \(u_n=199\), find the value of \(n\).
(ii)For this value of \(n\), find the sum \(S_n\).
Solutions:
(a) \(d=7\);
(b) \(n=28,~ S_{28}=2926\)
-
The general term of a geometric sequence is given by: \(u_n=512\cdot \left(\frac{3}{2}\right)^n\).
(a)Write down the common ratio.
(b)(i)Given that \(u_n=13\,122\), find the value of \(n\).
(ii)For this value of \(n\), find the sum \(S_n\).
Solutions:
(a) \(r=\frac{3}{2}\);
(b) \(n=8,~ S_{8}=37\,830\)
-
An arithmetic sequence has the terms: \(u_1=27\) and \(u_2=39\).
(a)Write down the common difference.
(b)Write down the \(10^{th}\) term.
(c)Write down the \(n^{th}\) term.
(d)Calculate the sum of the first 10 terms.
Solutions:
(a) \(d=12\);
(b) \(u_{10}=135\);
(c) \(u_n=15+12n\);
(d) \(S_{10}=810\)
-
In an arithmetic sequence \(u_1=1001\) and \(u_{15}=777\).
(a)Write down the \(n^{th}\) term.
(b)Find the number of positive terms.
(c)Write down the smallest positive term.
(d)Calculate the sum of all positive terms.
Solutions:
(a) \(u_n=1017-16n\);
(b) 63 positive terms;
(c) \(u_{63}=9\);
(d) \(S_{63}=31\,815\)
-
Numbers \(u_1=\sqrt{m},~ u_2=m-12\) and \(u_3=m+\sqrt{m}\) are the first three
terms of an arithmetic sequence.
(a)Find \(m\).
(b)Write down the general term.
(c)Given that the \(n^{th}\) term of this sequence is 600, find \(n\).
The sum of the first \(k\) terms is labelled \(S_k\).
(d)Find \(k\) so that \(S_k=15\,750\).
Solutions:
(a) \(m=36\);
(b) \(u_n=18n-12\);
(c) \(n=34\);
(d) \(k=42\)
-
In a geometric sequence \(u_1=2\) and \(u_2=10\).
(a)Find the common ratio.
(b)Write down the \(n^{th}\) term.
The first \(n\) terms of this sequence are less than \(10^{10}\).
(c)Find \(n\).
(d)Find the sum of the first \(n\) terms.
Solutions:
(a) \(r=5\);
(b) \(u_n=2\cdot 5^{n-1}\);
(c) \(n=14\);
(d) \(S_{14}=3\,051\,757\,812\)
-
Numbers \(u_1=m,~ u_2=m+3\) and \(u_3=m^2-2m+9\) are the first three terms of an infinite
geometric sequence.
(a)Find \(m\).
(b)Write down the \(n\)-th term.
(c)Some terms in this sequence have the value less than 1 million.
(i)Find how many terms have the value less than 1 million.
(ii)Find the lagest among these terms.
(iii)Calculate the sum of these terms.
Solutions:
(a) \(m=3\);
(b) \(u_n=3\cdot 2^{n-1}\);
(c)(i) 19 terms;
(ii) \(u_{19}=786\,432\);
(iii) \(S_{19}=1\,572\,861\)
-
The \(n\)-th term of a sequence is \(u_n=\frac{81}{8}\cdot\left(\frac{2}{3}\right)^{n-1}\).
(a)Write down terms \(u_4\) and \(u_5\).
(b)Show that this is a geometric sequence.
(c)Calculate the following two sums, giving your results in the form of a fraction:
(i)\({\displaystyle \sum\limits_{k=1}^6 u_k}\)
(ii)\({\displaystyle \sum\limits_{k=4}^7 u_k}\)
Solutions:
(a) \(u_4=3,~ u_5=2\);
(b) \(\frac{u_{n+1}}{u_n}=\frac{2}{3}=\mathrm{constant}\);
(c)(i) \(\frac{665}{24}\);
(ii) \(\frac{65}{9}\)
-
Consider the finite sequence with the terms: \(u_1=x+7,~ u_2=3x+9,~ u_3=9x+3\).
(a)Find \(x\) so that this will be a finite arithmetic sequence.
(b)Find \(x\) so that this will be a finite geometric sequence.
Solutions:
(a) \(x=2\), AS: 9, 15, 21;
(b) \(x=5\), GS: 12, 24, 48
-
(a)Andrew added the multiples of 2, from 2 to 2048. Find his sum:
\(a=2+4+6+8+10+\cdots+2048\)
(b)Barbie added the powers of 2, from 2 to 2048. Find her sum:
\(b=2+4+8+16+32+\cdots+2048\)
Solutions:
(a) \(a=1\,049\,600\);
(b) \(b=4094\)
-
In a finite arithmetic sequence the first term is 6 and the last term is 142.
The sum of all terms in this finite sequence is 666.
(a)Find the number of terms.
(b)Find the common difference.
(c)Write down all terms in this finite sequence.
Solutions:
(a) 9 terms;
(b) \(d=17\);
(c) 6, 23, 40, 57, 74, 91, 108, 125, 142.
-
A cinema has 15 rows of seats. There are 20 seats in the first row. Each successive row has one seat more than the previous row (second row: 21 seats,
third row 22 seats, etc.).
(a)Find the number of seats in the last row.
(b)Find the number of all seats in this cinema.
Solutions:
(a) 34 seats in the last row;
(b) 405 seats altogether
-
In the beginning of the year 2000 the kingdom of Zamunda had 4 891 000 inhabitants.
The population of this country increases at a growth rate of 26‰ per year.
(a)Find the number of inhabitants in the beginning of the year 2015.
(b)How many years does it take for the population to double?
Solutions:
(a) 7 188 000 inhabitants;
(b) 27 years
-
Microbiologists studied a specific cell culture. At 8:00 in the morning this cell culture contained 1700 cells.
At 12:00 there were 13500 cells already. Use exponential growth to model the growth of the population and answer the
following questions.
(a)Find the population at 13:17.
(b)How long does it take for the population to double? Write your answer in hours and minutes.
(c)When will the population exceed 90000? Write your answer in hours and minutes.
Solutions:
(a) 26245 cells;
(b) 1 hour and 20 minutes;
(c) at 15:40
-
In music, the equal-tempered chromatic scale is made of 12 basic tones. Each tone has its specific sound frequency which determines its pitch.
The tone A in the third octave has the frequency of 220 Hz. The ratio of frequencies of two consecutive tones is constant, so
the frequencies of the tones form a geometric sequence. This ratio is equal to \(r=\sqrt[{\scriptstyle 12}]{2}\).
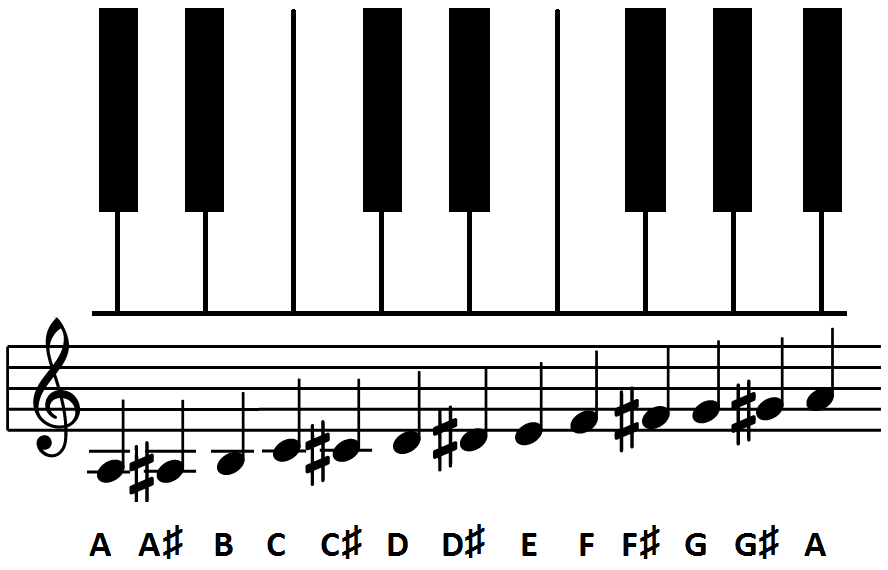
(a)Find frequencies of the following tones (round your results to the nearest integer):
(i)C
(ii)D
(iii)F sharp (also called Fis)
(b)Find the tone corresponding to the frequency of 392 Hz.
(c)Find the frequency of the tone which is one octave higher than a given tone.
Warning:
Tone called B in English, is called H in the rest of Europe.
Tone called B in the rest of Europe, is called A sharp or H flat
in English.
Solutions:
(a) C: 262 Hz, D: 294 Hz,
Fis: 370 Hz;
(b) G: 392 Hz;
(c) one octave higher tone has twice the frequency of the given tone
(A in the fourth octave has the frequency of 440 Hz)
-
Viktor Navorski deposited 2300 € in The National Bank of Krakozhia.
This bank compounds his deposit annually at 3% interest rate per annum.
(a)How much will he have in his account after 4 years?
(b)When will he have 3000 € in his account?
Solutions:
(a) He'll have 2588.67 €;
(b) in approximately 9 years
-
In beginning of 1995, Chuck Noland deposited 25000 € in Memphis Bank. In beginning of 2001
Chuck returned and discovered that he had 32000 € in his account. His bank compounded his deposit annually
at a fixed interest rate p.a.
(a)Find the interest rate p.a.
(b)How long would it take for his deposit to double? Round your result to the nearest integer.
Solutions:
(a) It's 4.2%;
(b) approximately 17 years
-
Colonel Sanders plans to open a restaurant and he needs money to start the business.
He will take out a loan of 20 000 € and now he is considering two different repayment
plans:
Plan A means that he will have to repay the loan in 3 years (in 36 monthly payments)
at interest rate of 6% p.a.
(a)Calculate his monthly payment according to plan A.
(b)Calculate the total amount of all his payments according to plan A.
Plan B means that he will have to repay the loan in 5 years (in 60 monthly payments)
at interest rate of 7.5% p.a.
(c)Calculate his monthly payment according to plan B.
(d)Calculate the total amount of all his payments according to plan B.
Solutions:
(a) 608.44 € monthly;
(b) total: 21 903.80 €
(c) 400.76 € monthly;
(d) total: 24 045.50 €
-
Ray Kroc plans to open a restaurant and he needs money, too.
He can take out a loan of 26 000 € at interest rate of 8% p.a., but he knows that he can't afford
to pay back more than 300 € monthly.
(a)Find the most appropriate number of monthly payments.
(b)Calculate his monthly payment according to this repayment plan.
(c)Calculate the total amount of all his payments in this case.
Solutions:
(a) 130 monthly payments;
(b) 299.66 € monthly;
(c) total: 38 955.40 €


