Quadratic function

Graph of the quadratic function

1. ?
   ?

   A quadratic function has the equation:
   
   $f(x)=a{x}^2+bx+c$
   
   Vertex and zeros can be calculated using formulas:
   
   $V(-\frac{b}{2a},-\frac{\mathrm{\Delta }}{4a})$
   
   $x_{1,2}=\frac{-b\pm \sqrt{\mathrm{\Delta }}}{2a}$
   
   where $\mathrm{\Delta }=b^2-4ac$ is the disciminant.
   Draw graphs of the following quadratic functions manually.
   In each case calculate the vertex and zeros, then draw the graph. Additionally you can use a table of values, too.
   

   (a)   $f(x)=x^2-1$

   (b)   $f(x)=x^2-4x$

   (c)   $f(x)=2x^2-8x+6$

   (d)   $f(x)=-x^2+2x-1$

   (e)   $f(x)=x^2+4x+5$

   Solutions:    (a)  $V(0,-1),x_1=-1,x_2=1$;     (b)  $V(2,-4),x_1=0,x_2=4$;     (c)  $V(2,-2),x_1=1,x_2=3$;     (d)  $V(1,0),x_1=x_2=1$;     (e)  $V(-2,1)$
2. Draw graphs of the following quadratic functions using your GDC.
   Then use the Analyze Graph option on your GDC to find the vertex and zeros.
   

   (a)   $f(x)=x^2-2x-3$

   (b)   $f(x)=x^2-x+\frac{1}{4}$

   (c)   $f(x)=2x^2-4x+4$

   (d)   $f(x)=-x^2+x$

   (e)   $f(x)=-x^2+5x-3$

   Solutions:    (a)  $V(1,-4),x_1=-1,x_2=3$;     (b)  $V(\frac{1}{2},0),x_1=x_2=\frac{1}{2}$;     (c)  $V(2,2)$;     (d)  $V(\frac{1}{2},\frac{1}{4}),x_1=0,x_2=1$;     (e)  $V(2.5,3.25),x_1\approx 0.697,x_2\approx 4.303$
3. ?
   ?

   $f(x)=a(x-x_1)(x-x_2)$ is called the zeros form of the quadratic function. Numbers $x_1$ and $x_2$ are the zeros.
   
   $f(x)=a(x-h{)}^2+k$ is called the vertex form of the quadratic function. Numbers $h$ and $k$ are the coordinates of the vertex $V(h,k)$.
   Draw the graph and write down the vertex and zeros of each of the following quadratic functions:
   

   (a)   $f(x)=(x-2)(x-4)$

   (b)   $f(x)=-2(x-2)(x-3)$

   Solutions:    (a)  $V(3,-1),x_1=2,x_2=4$;     (b)  $V(2.5,0.5),x_1=2,x_2=3$
4. Draw the graph and write down the vertex and zeros of each of the following quadratic functions:
   

   (a)   $f(x)=(x-2{)}^2-9$

   (b)   $f(x)=(x-3{)}^2+1$

   Solutions:    (a)  $V(2,-9),x_1=-1,x_2=5$;     (b)  $V(3,1)$
5. Quadratic function $f$ has the $x$-axis intercepts (zeros) $x_1=-3,x_2=1$ and passes through the point $P(2,-5)$.
   

   (a)   Write the equation of this quadratic function in the intercept form $f(x)=a(x-p)(x-q)$.

   (b)   Write the equation of this quadratic function in the standard form $f(x)=a{x}^2+bx+c$.

   (c)   Draw the graph of $f$.

   Solutions:    (a)  $f(x)=-1(x+3)(x-1)$;     (b)  $f(x)=-x^2-2x+3$
6. Quadratic function $f$ has the vertex $V(2,-4)$ and passes through the point $P(6,4)$.
   

   (a)   Write the equation of this quadratic function in the vertex form $f(x)=a(x-h{)}^2+k$.

   (b)   Write the equation of this quadratic function in the standard form $f(x)=a{x}^2+bx+c$.

   (c)   Draw the graph of $f$.

   Solutions:    (a)  $f(x)=\frac{1}{2}(x-2{)}^2-4$;     (b)  $f(x)=\frac{1}{2}{x}^2-2x-2$
7. Find the points of intersection of the following two graphs:
   

   (a)   $y=x^2-6x+8,y=x+2$

   (b)   $y=x^2-x-2,y=x-3$

   Solutions:    (a)  $P_1(1,3),P_2(6,8)$;     (b)  $P(1,-2)$
8. Find the points of intersection of the following two graphs:
   

   (a)   $y=x^2-2x-3,y=-x^2+1$

   (b)   $y=x^2-4x,y=\frac{1}{2}{x}^2-x-\frac{5}{2}$

   Solutions:    (a)  $P_1(-1,0),P_2(2,-3)$;     (b)  $P_1(1,-3),P_2(5,5)$
9. Find all the values of $x$ for which the given function is negative:
   

   (a)   $y=x^2-5x+4$

   (b)   $y=x^2-2x+2$

   Hint:    Draw the graph.
   Solutions:    (a)  $1<x<4$;     (b)  $x$ doesn't exist (this function is always positive)
10. Solve the inequalities:
    

    (a)   $x^2-2x-3⩽0$

    (b)   $x^2-6x+9>0$

    Solutions:    (a)  $-1⩽x⩽3$;     (b)  any $x\ne 3$

Quadratic equation

11. ?
    ?

    Quadratic equation $a{x}^2+bx+c=0$ can be solved using the formula:
    
    $x_{1,2}=\frac{-b\pm \sqrt{\mathrm{\Delta }}}{2a}$
    
    where $\mathrm{\Delta }=b^2-4ac$ is the disciminant.
    Solve the following equations manually.
    First calculate the discriminant, then use the quadratic formula.
    

    (a)   $x^2-5x+6=0$

    (b)   $x^2=x+2$

    (c)   $2x^2+1=3x$

    (d)   $12x-9x^2=4$

    (e)   $5x^2=x-2$

    Solutions:    (a)  $x_1=2,x_2=3(\mathrm{\Delta }=1)$;     (b)  $x_1=-1,x_2=2(\mathrm{\Delta }=9)$;     (c)  $x_1=\frac{1}{2},x_2=1(\mathrm{\Delta }=1)$;     (d)   one repeated root: $x_1=x_2=\frac{2}{3}(\mathrm{\Delta }=0)$;     (e)  no real roots $(\mathrm{\Delta }=-39)$
12. Solve the following equations with your GDC.
    First draw the graph(s), then use the Analyze Graph tool.
    

    (a)   $x^2=2x+3$

    (b)   $3x^2+x=2$

    (c)   $4x^2-4x+1=0$

    (d)   $2x^2+2=3x$

    Solutions:    (a)  $x_1=-1,x_2=3$;     (b)  $x_1=-1,x_2\approx 0.667$;     (c)  $x_1=x_2=\frac{1}{2}=0.5$;     (d)  no real roots, $x$ doesn't exist
13. Solve the following equations with your GDC.
    Use the PolyRoots tool.
    

    (a)   $x^2-4x+3=0$

    (b)   $3x^2+6=11x$

    (c)   $2x^2=8x-8$

    (d)   $x^2+5=2x$

    Solutions:    (a)  $x_1=1,x_2=3$;     (b)  $x_1\approx 0.667,x_2=3$;     (c)  $x_1=x_2=2$;     (d)  no real roots, $x$ doesn't exist
14. Solve the following equations. Write your answers correct to three significant figures:
    

    (a)   $2x(x-7)+15=0$

    (b)   $(2x+1)(x-2)=(x+1{)}^2$

    Solutions:    (a)  $x_1\approx 5.68,x_2\approx 1.32$;     (b)  $x_1\approx 5.54,x_2\approx -0.541$
15. Solve the following equations:
    

    (a)   $5x-4=\frac{1}{x}$

    (b)   $x-2=\frac{20}{x-1}$

    (c)   ${\displaystyle \frac{x}{x-2}=\frac{4}{x-5}}$

    Solutions:    (a)  $x_1=-\frac{1}{5}=-0.2,x_2=1$;     (b)  $x_1=-3,x_2=6$;     (c)  $x_1=1,x_2=8$
16. Solve the following equations:
    

    (a)   $2x^4-5x^2-12=0$

    (b)   $(x^2+1{)}^2-12(x^2+1)+20=0$

    (c)   $x-7\sqrt{x}+10=0$

    Solutions:    (a)  $x_1=2,x_2=-2$;     (b)  $x_1=1,x_2=-1,x_3=3,x_4=-3$;     (c)  $x_1=4,x_2=25$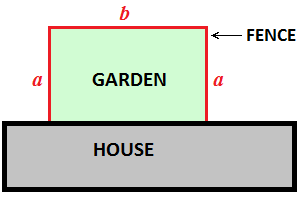

Applications of quadratic function and equation

17. The product of two positive numbers is 120. The first number is 7 more than the other. Find these two numbers.
    Solutions:    $a=15,b=8$
18. The product of two positive numbers is 403. The first number is 5 more than twice the other number. Find these two numbers.
    Solutions:    $a=31,b=13$
19. The product of two numbers is 360. The first number is 3 more than one half of the other number. Find these two numbers.
    Solutions:    $a_1=15,b_1=24$;     $a_2=-12,b_2=-30$
20. The area of a rectangle is $2100{\mathrm{cm}}^2$. If the side $a$ were $10\mathrm{cm}$ longer it would be twice as long as the side $b$. Find the lengths of sides $a$ and $b$.
    Solutions:    $a=60\mathrm{cm},b=35\mathrm{cm}$
21. A farmer has two fields. Each of them has the form of a square. The side of the first field is $20\mathrm{m}$ longer than the other. Both fields together have the area of $51400{\mathrm{m}}^2$. Determine the area of the first field and the area of the second field.
    Solutions:    $a^2=28900{\mathrm{m}}^2,b^2=22500{\mathrm{m}}^2$
22. Alexis has a rectangular garden right next to her house. She bought 12 m of fence and decided to put it around her garden on three sides. She won't put fence on the side where the wall of the house is (see picture).
    

    Her first idea was to use equal lengths for sides $a$ and $b$.

    (a)   Find $a$ and $b$ in this case.

    (b)   Calculate the area in this case.

    Then she started thinking of another interesting idea. Help her develop this idea:

    (c)   Express value of $b$ with $a$.

    (d)   Write down the area as a function of variable $a$.

    (e)   Use your GDC to draw this function.

    (f)   Find out, for which $a$ this garden has the largest area. Write the corresponding $b$ and area, too

    Solutions:    (a)  $a=b=4\mathrm{m}$;     (b)  $A=16{\mathrm{m}}^2$;
    (c)  $b=12-2a$;     (d)  $A=-2a^2+12a$;     (f)  $a=3\mathrm{m},b=6\mathrm{m},$ $A=18{\mathrm{m}}^2$

 Index