(a) \(p(x)=x^3+2x^2-15x\)
(b) \(p(x)=x^3-5x^2-4x+20\)
(c) \(p(x)=x^4-3x^3-x^2+3x\)
Solutions: (a) \(x_1=0,~ x_2=3,~ x_3=-5\); (b) \(x_1=2,~ x_2=-2,~ x_3=5\); (c) \(x_1=0,~ x_2=1,~ x_3=-1,~ x_4=3\)(a) \(p(x)=x^3-2x^2-4x+8\)
(b) \(p(x)=x^4-4x^2\)
(c) \(p(x)=x^5-4x^4+4x^3\)
Solutions: (a) \(x_{1,2}=2,~ x_3=-2\); (b) \(x_{1,2}=0,~ x_3=2,~ x_4=-2\); (c) \(x_{1,2,3}=0,~ x_{4,5}=2\)(a) \(p(x)=x^3-x^2-14x+24\)
(b) \(p(x)=x^4-x^3-9x^2-11x-4\)
(c) \(p(x)=x^5-3x^4-5x^3+15x^2+4x-12\)
(d) \(p(x)=x^5-2x^4-5x^3+10x^2+4x-8\)
(e) \(p(x)=x^5-5x^4+4x^3-20x^2\)
Solutions: (a) \(x_1=2,~ x_2=3,~ x_3=-4\); (b) \(x_1=4,~ x_{2,3,4}=-1\); (c) \(x_1=-1,~ x_2=1,~ x_3=-2,~ x_4=2,~ x_5=3\); (d) \(x_{1,2}=2,~ x_3=-2,~ x_4=-1,~ x_5=1\); (e) \(x_{1,2}=0,~ x_3=5\)(a) \(p(x)=x^3+x^2-2x\)
(b) \(p(x)=x^3-3x\)
(c) \(p(x)=x^4-5x^2+4\)
(d) \(p(x)=x^5-4x^3+3x\)
Solutions: (a) \(x_1=0,~ x_2=1,~ x_3=-2\); (b) \(x_1=0,~ x_2=\sqrt{3}\approx1.73,~ x_3=-\sqrt{3}\approx-1.73\); (c) \(x_1=1,~ x_2=-1,~ x_3=2,~ x_4=-2\); (d) \(x_1=0,~ x_2=1,~ x_3=-1,~ x_4=\sqrt{3}\approx1.73,~ x_5=-\sqrt{3}\approx-1.73\)(a) \(p(x)=x^4-5x^3+6x^2\)
(b) \(p(x)=x^4+x^3-2x^2\)
(c) \(p(x)=x^4-2x^3\)
(d) \(p(x)=x^5+4x^4+4x^3\)
Solutions: (a) \(x_{1,2}=0,~ x_3=2,~ x_4=3\); (b) \(x_{1,2}=0,~ x_3=1,~ x_4=-2\); (c) \(x_{1,2,3}=0,~ x_4=2\); (d) \(x_{1,2,3}=0,~ x_{4,5}=-2\)(a) Using GDC find zeros.
(b) Using GDC find \(f(0),~ f(-3),~ f(\frac{1}{2})\) and \(f(3.4)\).
(c) Using GDC find extreme points (maxima and minima).
Solutions: (a) zero: \(x_1=-1\); (b) \(f(0)=5,~ f(-3)=-76,\) \(f(\frac{1}{2})=\frac{9}{2}=4.5,~ f(3.4)\approx48.9\); (c) maximum \(P_1(0,5)\), minimum \(P_2(1,4)\)(a) Draw the graph of this polynomial.
(b) Write down zeros.
(c) Calculate \(p(0.02),~ p(\sqrt{3}),~ p(321)\).
(d) Find extreme points (maxima and minima).
Solutions: (b) zero: \(x_1\approx1.75\); (c) \(p(0.02)\approx-0.981,~ p(\sqrt{3})\approx-0.0718,~ p(321)\approx3.29\cdot10^7\); (d) maximum \(P_1(0.333,-0.852)\), minimum \(P_2(1,-1)\)(a) Find \(m\).
(b) Draw the graph of this polynomial.
(c) Write down zeros.
(d) Find all values of \(x\) where \(p(x)=3\).
(e) Find extreme points (maxima and minima).
Solutions: (a) \(m=4\); (c) zeros: \(x_1=-1,~ x_{2,3}=2\); (d) \(x\approx-0.532,~ x\approx0.653,~ x\approx2.88\); (e) maximum \(P_1(0,4)\), minimum \(P_2(2,0)\)(a) Find \(a\) and \(b\).
(b) Draw the graph of this polynomial.
(c) Write down zeros.
This polynomial can be written as \(p(x)=(x-2)^3+m\).
(d) Find \(m\).
Solutions: (a) \(a=12,~ b=-5\); (c) zero: \(x_1\approx 0.558\); (d) \(m=3\)(a) Find \(a,~ b\) and \(c\).
(b) Draw the graph of this function.
(c) Write the coordinates of extreme points.
Solutions: (a) \(a=-5,~ b=3,~ c=4\); (c) max.: \(P_1(0.333,4.48)\), min.: \(P_2(3,-5)\)(a) \({\displaystyle\lim_{x\to\infty}\frac{2x+3}{x-1}}\)
(b) \({\displaystyle\lim_{x\to\infty}\frac{x+2}{3x+5}}\)
(c) \({\displaystyle\lim_{x\to-\infty}\frac{5+6x}{1-4x}}\)
Solutions: (a) \(\cdots=2\); (b) \(\cdots=\frac{1}{3}\); (c) \(\cdots=-\frac{3}{2}\)(a) \({\displaystyle\lim_{x\to\infty}\frac{x^2+x+1}{x^2+5x}}\)
(b) \({\displaystyle\lim_{x\to-\infty}\frac{2x^2-x}{x^2+1}}\)
(c) \({\displaystyle\lim_{x\to\pm\infty}\frac{(x+1)^2}{2x(x+2)}}\)
(d) \({\displaystyle\lim_{x\to\pm\infty}\frac{3x^3+1}{(x+1)^3}}\)
Solutions: (a) \(\cdots=1\); (b) \(\cdots=2\); (c) \(\cdots=\frac{1}{2}\); (d) \(\cdots=3\)(a) \({\displaystyle\lim_{x\to\infty}\frac{x^2+2x}{x^3+1}}\)
(b) \({\displaystyle\lim_{x\to\infty}\frac{1}{x^2+1}}\)
(c) \({\displaystyle\lim_{x\to\infty}\frac{x^2}{2x+3}}\)
Solutions: (a) \(\cdots=0\); (b) \(\cdots=0\); (c) Not possible – the limit doesn't exist.(a) \({\displaystyle f(x)=\frac{x+1}{x-1}}\)
(b) \({\displaystyle f(x)=\frac{2x-3}{x-1}}\)
(c) \({\displaystyle f(x)=\frac{x+1}{2x+5}}\)
Solutions: (a) zero: \(x=-1\), vertical asymptote: \(x=1\), horizontal asymptote: \(y=1\); (b) zero: \(x=\frac{3}{2}\), vertical asymptote: \(x=1\), horizontal asymptote: \(y=2\); (c) zero: \(x=-1\), vertical asymptote: \(x=-\frac{5}{2}\), horizontal asymptote: \(y=\frac{1}{2}\);(a) \({\displaystyle f(x)=\frac{1}{x+2}}\)
(b) \({\displaystyle f(x)=\frac{2}{3x-4}}\)
(c) \({\displaystyle f(x)=\frac{1}{1-x}}\)
Solutions: (a) zero: /, vertical asymptote: \(x=-2\), horizontal asymptote: \(y=0\); (b) zero: /, vertical asymptote: \(x=\frac{4}{3}\), horizontal asymptote: \(y=0\); (c) zero: /, vertical asymptote: \(x=1\), horizontal asymptote: \(y=0\);(a) write down the zero, vertical asymptote and horizontal asymptote,
(b) draw the graph,
(c) write the domain and range.
Solutions: (a) zero: \(x=1\), vertical asymptote: \(x=\frac{1}{2}\), horizontal asymptote: \(y=\frac{3}{2}\); (c) domain: \(x\ne\frac{1}{2}\), range: \(y\ne\frac{3}{2}\)(a) write down the zero, vertical asymptote and horizontal asymptote,
(b) draw the graph,
(c) write the domain and range,
(d) find \(f^{-1}(x)\).
Solutions: (a) zero: \(x=1\), vertical asymptote: \(x=-2\), horizontal asymptote: \(y=-1\); (c) domain: \(x\ne-2\), range: \(y\ne-1\); (d) \(f^{-1}(x)=\frac{-2x+1}{x+1}\)(a) Draw the graph.
(b) Find zeros, vertical asymptotes and horizontal asymptote.
(c) Find the point where the graph intersects the horizontal asymptote.
Solutions: (b) zero \(x_{1,2}=0\), vertical asymptotes \(x=1\) and \(x=-2\), horizontal asymptote \(y=1\); (c) intersection: \(P(2,1)\)(a) Draw the graph.
(b) Find zeros, vertical asymptotes and horizontal asymptote.
(c) Find the point where the graph intersects the horizontal asymptote.
(d) Find the extreme points.
Solutions: (b) zero \(x_{1,2}=-2\), vertical asymptotes \(x=1\) and \(x=-1\), horizontal asymptote \(y=1\); (c) intersection: \(P(-1.2,1)\); (d) min.: \((-2,0)\), max.: \((-0.5,-3)\)(a) Draw the graph.
(b) Find zeros, vertical asymptotes and horizontal asymptote.
(c) Find the extreme points.
Solutions: (b) zero \(x_1=-1\), vertical asymptotes \(x_{1,2}=0\), horizontal asymptote \(y=0\); (c) min.: \((-2,-0.25)\)(a) Draw the graph.
(b) Find zeros, vertical asymptotes and horizontal asymptote.
(c) Find the extreme points. Round the coordinates to three decimals.
Solutions: (b) zero \(x_1=1\), vertical asymptotes \(x=-1\) and \(x=-4\), horizontal asymptote \(y=0\); (c) min.: \((-2.162,1.481)\), max.: \((4.162,0.075)\)(a) Draw the graph.
(b) Find zeros, vertical asymptotes and horizontal asymptote.
(c) Hence or otherwise, find the limit: \({\displaystyle \lim_{x\to\infty} \frac{x^2-3x}{x^2+1}}\)
Solutions: (b) zeros \(x_1=0,~ x_2=3\), vertical asymptotes don't exist, horizontal asymptote \(y=1\); (c) limit = 1(a) Draw the graph.
(b) Find zeros, vertical asymptotes and horizontal asymptote.
Solutions: (b) zeros \(x_{1,2}=0,~ x_3=2\), vertical asymptote \(x=1\), horizontal asymptote doesn't exist(a) Draw the graph.
(b) Write down vertical asymptotes and horizontal asymptote.
(c) Write down zeros (using GDC).
(d) Find the zeros algebraically and write down the exact values.
Solutions: (b) vertical asymptotes \(x=1\) and \(x=-1\), horizontal asymptote \(y=1\); (c) zeros \(x_1\approx-0.414,~ x_2\approx2.41\); (d) zeros: \(x_1=1-\sqrt{2},~ x_2=1+\sqrt{2}\)(a) Write down the horizontal asymptote.
The line \(x=3\) is a vertical asymptote of this function.
(b) Find the value of \(q\).
(c) Draw the graph of this function.
Solutions: (a) horizontal asymptote \(y=2\); (b) \(q=3\)(a) Write down the horizontal asymptote.
(b) Find the value of \(q\).
(c) Find the \(y\)-axis intercept of this function.
Solutions: (a) horizontal asymptote \(y=\frac{1}{2}\); (b) \(q=4\); (c) \(y=-\frac{1}{2}\)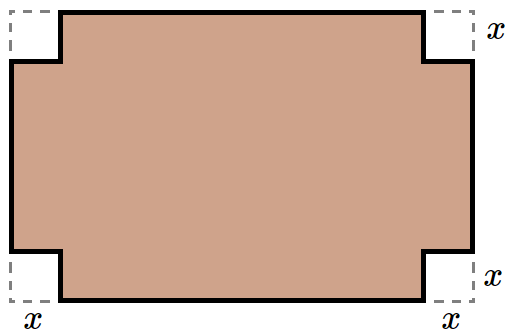
We have a rectangular piece of cardboard with dimensions \(80\times60~\mathrm{cm}\).
We'd like to make a box out of this piece of cardboard. We'll cut off a small square at each corner, fold the sides
and glue them together.
(a) Write the volume of this box as a function of \(x\) (= the side of the small square).
(b) Draw this function in a coordinate system with appropriate units.
(c) Find the value of \(x\) where the volume is maximal.
(d) Write down the maximal volume (in \(\mathrm{cm}^3\) and in \(\ell\)).
Solutions: (a) \(V=x(80-2x)(60-2x)\); (b) (use \(x\) from −10 to 50, \(y\) from −5000 to 25000); (c) \(x\approx11.3~\mathrm{cm}\); (d) \(V\approx24258~\mathrm{cm}^3\approx24.3\,\ell\)(a) Draw this function in a coordinate system with appropriate units.
(b) Find the value of \(x\) where the concentration is maximal. Write \(x\) in hours and minutes.
(c) Write down the maximal concentration (in \(\mathrm{mg}/\ell\)).
(d) When is the concentration equal to one half of the maximal value? Write the time in hours and minutes.
Solutions: (b) \(x_{\mathrm{max}}\approx2\,\mathrm{h}\,14\,\mathrm{min}\); (c) \(y_{\mathrm{max}}\approx19.0~\mathrm{mg}/\ell\); (d) \(x_1\approx0\,\mathrm{h}\,36\,\mathrm{min}\), \(x_2\approx8\,\mathrm{h}\,21\,\mathrm{min}\)(a) Draw the values as points in a coordinate system with appropriate units.
(b) Find an appropriate function \(y=f(x)\) which can be used for modelling his results.
Hint: Use the function \(y=x^2\) and apply transformations (stretch, shift) to adjust the graph.(a) Draw the values as points in a coordinate system with appropriate units.
(b) Find an appropriate function \(y=f(x)\) which can be used for modelling her results.
Hint: Use the function \(y=x^3\) and apply transformations (stretch, shift) to adjust the graph.