
(a) \(y=x^2+1\)
(b) \(y=x^2+3\)
(c) \(y=x^2-2\)
Solutions: (a) Translation of 1 unit parallel to the \(y\)-axis (shift 1 unit upwards); (b) translation of 3 units parallel to the \(y\)-axis (shift 3 units upwards); (c) translation of −2 units parallel to the \(y\)-axis (shift 2 units downwards)(a) Shift this function 4 units upwards. Write down the equation of the new function and draw the graph.
(b) Shift this function 1 unit downwards. Write down the equation of the new function and draw the graph.
Solutions: (a) \(y=x^3-x+4\); (b) \(y=x^3-x-1\)(a) \(y=(x-1)^2\)
(b) \(y=(x-2)^2\)
(c) \(y=(x+3)^2\)
Solutions: (a) Translation of 1 unit parallel to the \(x\)-axis (shift 1 unit to the right); (b) translation of 2 units parallel to the \(x\)-axis (shift 2 units to the right); (c) translation of −3 units parallel to the \(x\)-axis (shift 3 units to the left)(a) Shift this function 2 units to the right. Write down the equation of the new function and draw the graph.
(b) Shift this function 1 unit to the left. Write down the equation of the new function and draw the graph.
Solutions: (a) \(y=(x-2)^3-(x-2)\); (b) \(y=(x+1)^3-(x+1)\)(a) \(y=f(x)+1\)
(b) \(y=f(x)-2\)
(c) \(y=f(x-3)\)
(d) \(y=f(x+2)\)
(e) \(y=f(x-2)-3\)
Solutions: (a) \(y=x^3-3x+3\), shift 1 unit upwards; (b) \(y=x^3-3x\), shift 2 units downwards; (c) \(y=(x-3)^3-3(x-3)+2\), shift 3 units to the right; (d) \(y=(x+2)^3-3(x+2)+2\), shift 2 units to the left; (e) \(y=(x-2)^3-3(x-2)-1\), shift 2 units to the right and 3 units downwards(a) Using your GDC draw the graph of the function \(f\).
Consider the function \(g(x)=f(x+4)+2\)
(b) Write the equation of the function \(g\). Simplify this equation.
(c) Use your GDC to draw the graph of the function \(g\).
Solutions: (b) \(g(x)=-(x+4)^2+4(x+4)-3+2\), simplified: \(g(x)=-x^2-4x-1\)(a) \(y=2\,f(x)\)
(b) \(y=3\,f(x)\)
(c) \(y=\frac{1}{2}\,f(x)\)
Solutions: (a) Dilation along the \(y\)-axis by a scale factor 2 (stretch in \(y\) by 2); (b) dilation along the \(y\)-axis by a scale factor 3 (stretch in \(y\) by 3); (c) dilation along the \(y\)-axis by a scale factor \(\frac{1}{2}\) (stretch in \(y\) by \(\frac{1}{2}\))(a) \(y=-\,f(x)\)
(b) \(y=-2\,f(x)\)
(c) \(y=-\frac{1}{2}\,f(x)\)
Solutions: (a) Dilation along the \(y\)-axis by a scale factor −1 = reflection in the \(x\)-axis (flip upside down); (b) dilation along the \(y\)-axis by a scale factor −2 (flip upside down and stretch in \(y\) by 2); (c) dilation along the \(y\)-axis by a scale factor \(-\frac{1}{2}\) (flip upside down and stretch in \(y\) by \(\frac{1}{2}\))(a) Using your GDC draw the graph of the function \(f\).
Consider the function \(g(x)=\frac{1}{2}f(x)\)
(b) Write the equation of the function \(g\). Simplify this equation.
(c) Use your GDC to draw the graph of the function \(g\).
Solutions: (b) \(g(x)=\frac{1}{2}(x^2-4x)\), simplified: \(g(x)=\frac{1}{2}x^2-2x\)(a) \(y=f(\frac{x}{2})\)
(b) \(y=f(\frac{x}{3})\)
(c) \(y=f(2x)\)
Solutions: (a) Dilation along the \(x\)-axis by a scale factor 2 (stretch in \(x\) by 2); (b) dilation along the \(x\)-axis by a scale factor 3 (stretch in \(x\) by 3); (c) dilation along the \(x\)-axis by a scale factor \(\frac{1}{2}\) (stretch in \(x\) by \(\frac{1}{2}\))(a) \(y=f(-x)\)
(b) \(y=f(-2x)\)
(c) \(y=f(-\frac{x}{2})\)
Solutions: (a) Dilation along the \(x\)-axis by a scale factor −1 = reflection in the \(y\)-axis (flip left-to-right); (b) dilation along the \(x\)-axis by a scale factor \(-\frac{1}{2}\) (flip left-to-right and stretch in \(x\) by \(\frac{1}{2}\)); (c) dilation along the \(x\)-axis by a scale factor −2 (flip left-to-right and stretch in \(x\) by 2)(a) \(y=f(x)-2\)
(b) \(y=f(x-2)\)
(c) \(y=2f(x)\)
(d) \(y=-\frac{1}{2}f(x)\)
(e) \(y=f\left(\frac{1}{2}x\right)\)
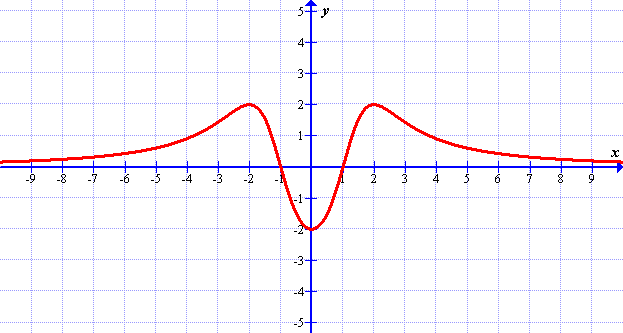
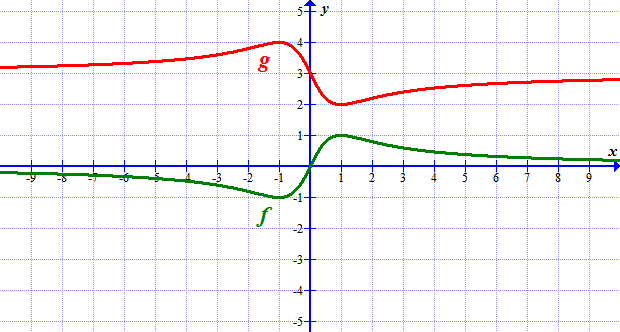
(a) Describe transformations required to transform \(f\) to \(g\).
(b) Write the equation of the function \(g\).
(c) Use your GDC to verify the equation you've just written.
Solutions: (a) Flip upside-down followed by a vertical shift by 3 units; (b) \(g(x)=3-\frac{2x}{x^2+1}\)(a) \(f(x)=2x+1\)
(b) \(f(x)=3x-2\)
(c) \(f(x)=\frac{1}{4}x+\frac{1}{2}\)
Solutions: (a) \(f^{-1}(x)=\frac{x-1}{2}\); (b) \(f^{-1}(x)=\frac{x+2}{3}\); (c) \(f^{-1}(x)=4x-2\)(a) \(f(x)=x^3+2\)
(b) \(f(x)=2x^3\)
(c) \(f(x)=\frac{1}{4}x^3\)
Solutions: (a) \(f^{-1}(x)=\sqrt[3]{x-2}\); (b) \(f^{-1}(x)=\sqrt[3]{\frac{x}{2}}\); (c) \(f^{-1}(x)=\sqrt[3]{4x}\)(a) \(f(x)=2^x\)
(b) \(f(x)=2^x+1\)
(c) \(f(x)=2^{x+1}\)
Solutions: (a) \(f^{-1}(x)=\log_2 x\); (b) \(f^{-1}(x)=\log_2 (x-1)\); (c) \(f^{-1}(x)=\log_2 x-1\)(a) write down the inverse function \(f^{-1}(x)\)
(b) draw graphs of \(f(x)\) and \(f^{-1}(x)\) in the same coordinate system.
Solutions: (a) \(f^{-1}(x)=x^3-3\)(a) \({\displaystyle f(x)=\frac{x+5}{3x-2}}\)
(b) \({\displaystyle f(x)=\frac{3x}{x-2}}\)
Solutions: (a) \(f^{-1}(x)=\frac{2x+5}{3x-1}\); (b) \(f^{-1}(x)=\frac{2x}{x-3}\)(a) \({\displaystyle f(x)=\frac{x-5}{x+2}}\)
(b) \({\displaystyle f(x)=\frac{1+x}{1-x}}\)
Solutions: (a) \(f^{-1}(x)=\frac{2x+5}{-x+1}\); (b) \(f^{-1}(x)=\frac{x-1}{x+1}\)(a) \({\displaystyle f(x)=\frac{x+2}{x-1}}\)
(b) \({\displaystyle f(x)=\frac{2x}{x-2}}\)
Solutions: (a) \(f^{-1}(x)=\frac{x+2}{x-1}\); (b) \(f^{-1}(x)=\frac{2x}{x-2}\) — in both cases \(f^{-1}(x)=f(x)\)(a) \(f(x^{-1})\)
(b) \(\big(f(x)\big)^{-1}\)
(c) \(f^{-1}(x)\)
Solutions: (a) \(f(x^{-1})=\frac{5x-2}{4x-3}\); (b) \(\big(f(x)\big)^{-1}=\frac{3x-4}{2x-5}\); (c) \(f^{-1}(x)=\frac{4x-5}{3x-2}\)(a) for \(x\geqslant 0\),
(b) for \(x\leqslant 0\).
Solutions: (a) \(f^{-1}(x)=\sqrt{x+3}\); (b) \(f^{-1}(x)=-\sqrt{x+3}\)