Functions

Domain and range

1. ?
   ?

   Domain of a function is the set of all \(x\) values for which the function is defined.
   Find the domain of the following functions:
   

   (a)   \(f(x)=\sqrt{x+2}\)

   (b)   \(f(x)=\sqrt{2x-3}\)

   (c)   \(f(x)=\sqrt{6-2x}\)

   Solutions:    (a)  domain: \(x\geqslant -2\);     (b)  domain: \(x\geqslant \frac{3}{2}\);     (c)  domain: \(x\leqslant3\)
2. Find the domain of the following functions:
   

   (a)   \(f(x)=\log_2 (x+3)\)

   (b)   \(f(x)=\log_\sqrt{5} (6-x)\)

   (c)   \(f(x)=\ln(5-2x)\)

   Solutions:    (a)  domain: \(x\gt -3\);     (b)  domain: \(x\lt6\);     (c)  domain: \(x\lt \frac{5}{2}\)
3. Use your GDC to draw the graph and then find the domain of the following functions:
   

   (a)   \(f(x)=\sqrt{4-x^2}\)

   (b)   \({\displaystyle f(x)=\sqrt{\frac{1-x}{1+x}}}\)

   (c)   \({\displaystyle f(x)=\frac{2x}{x^2+2}}\)

   Solutions:    (a)  domain: \(-2\leqslant x\leqslant 2\);     (b)  domain: \(-1\lt x\leqslant 1\);     (c)  domain: \(\mathbb{R}\)
4. Find the domain of the following functions:
   

   (a)   \({\displaystyle f(x)=\frac{x+2}{x^2-x}}\)

   (b)   \({\displaystyle f(x)=\sqrt{\frac{x+5}{3}}}\)

   (c)   \(f(x)=\log_3 x + 1\)

   Solutions:    (a)  domain: \(x\ne0,~ x\ne1\);     (b)  domain: \(x\geqslant -5\);     (c)  domain: \(x\gt 0\)
5. ?
   ?

   Range of a function is the set of all \(y\) values which are the results of this function.
   Use your GDC to draw the graph and then find the range of the following functions:
   

   (a)   \(f(x)=x^2-2\)

   (b)   \({\displaystyle f(x)=\frac{1}{x^2+1}}\)

   (c)   \(f(x)=x^3-4x\)

   Solutions:    (a)  range: \(y\geqslant -2\);     (b)  range: \(0\lt y\leqslant 1\);     (c)  range: \(\mathbb{R}\)
6. Use your GDC to draw the graph and then find the domain and range of the following functions:
   

   (a)   \(f(x)=e^x-2\)

   (b)   \({\displaystyle f(x)=\ln\frac{2-x}{2+x}}\)

   (c)   \({\displaystyle f(x)=\frac{x+1}{x-2}}\)

   (d)   \(f(x)=\sqrt[\scriptstyle 3]{x}\)

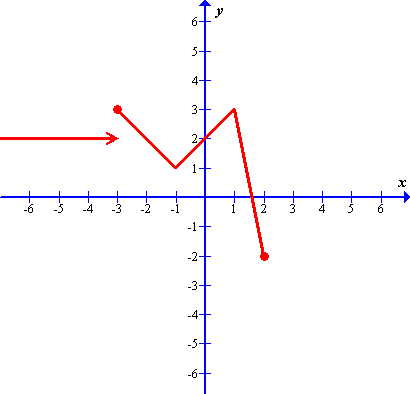
   Solutions:    (a)  domain: \(\mathbb{R}\), range: \(y\gt-2\);     (b)  domain: \(-2\lt x\lt2\), range: \(\mathbb{R}\);     (c)  domain: \(x\ne 2\), range: \(y\ne 1\);     (d)  domain: \(\mathbb{R}\), range: \(\mathbb{R}\)
7. Draw the graph of the function \(f(x)=\frac{\textstyle 1}{\textstyle x}\), for \(x\geqslant 1\) and then find the range of this function.
   Solution:    range: \(0\lt y\leqslant 1\)
8. Determine the range of the function \(f(x)=x^2\), for \(-1\leqslant x\leqslant 2\).
   Solution:    range: \(0\leqslant y\leqslant 4\)
9. Determine the range of the function \(f(x)=2^x\), for \(-2\leqslant x\leqslant 3\).
   Solution:    range: \(0.25\leqslant y\leqslant 8\)
10. Determine the range of the function \(f(x)=2x-5\), for \(x\geqslant 1\).
    Solution:    range: \(y\geqslant -3\)
11. Determine the domain and range of the following functions.
    

    (a)        (b)

    Solutions:    (a)  domain: \(\mathbb{R}\), range: \(-1\leqslant y\leqslant 3\);     (b)  domain: \(x\ne-1,~ x\ne 1\), range: \(y\leqslant -1,~ y\gt 0\)

Piecewise-defined functions

12. Draw graphs of the following piecewise-defined functions:
    

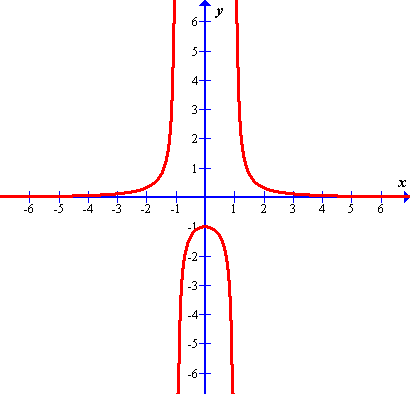
    (a)   \(f(x)= \left\{\begin{array}{cl} x^2; & \mathrm{for}~ x\leqslant 1 \cr 2-x; & \mathrm{for}~ x\gt 1 \end{array} \right.\)

    (b)   \(f(x)= \left\{\begin{array}{cl} 2^x; & \mathrm{for}~ x\lt 1 \cr x; & \mathrm{for}~ x\geqslant 1 \end{array} \right.\)

    Solutions: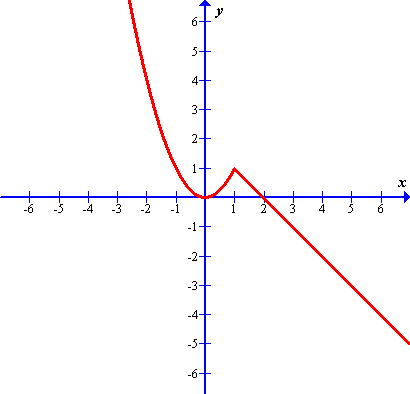
    
    (a)        (b)
13. Draw graphs and find the domain and range of the following functions:
    

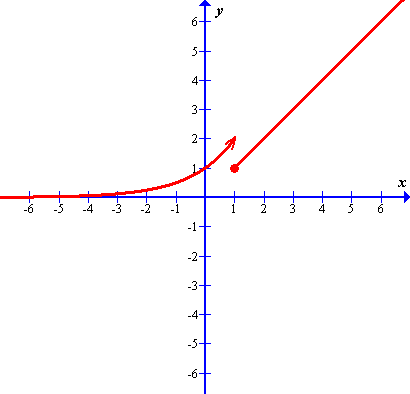
    (a)   \(f(x)= \left\{\begin{array}{cl} -1; & \mathrm{for}~ x\lt -1 \cr x; & \mathrm{for}~ -1\leqslant x\leqslant 1 \cr 1; & \mathrm{for}~ x\gt 1 \end{array} \right.\)

    (b)   \(f(x)= \left\{\begin{array}{cl} -x; & \mathrm{for}~ x\leqslant 0 \cr \frac{\textstyle 1}{\textstyle x}; & \mathrm{for}~ x\gt 0 \end{array} \right.\)

    (c)   \(f(x)= \left\{\begin{array}{cl} x+1; & \mathrm{for}~ 0\lt x\lt 2 \cr 1; & \mathrm{for}~ x\geqslant 2 \end{array} \right.\)

    Solutions:    (a)  domain: \(\mathbb{R}\), range: \(-1\leqslant y\leqslant 1\);     (b)  domain: \(\mathbb{R}\), range: \(y\geqslant 0\);     (c)  domain: \(x\gt 0\), range: \(1\leqslant y\lt 3\)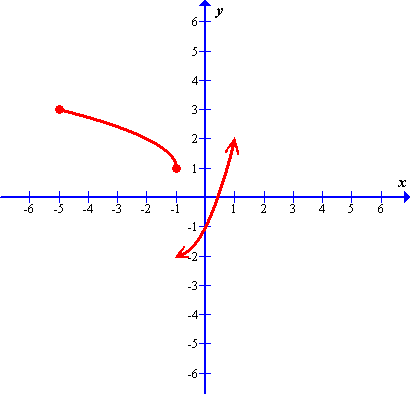
14. Determine the domain and range of the following functions.
    

    (a)        (b)

    Solutions:    (a)  domain: \(-5\leqslant x\lt 1\), range: \(-2\lt y\leqslant 3\);     (b)  domain: \(x\leqslant2\), range: \(-2\leqslant y\leqslant 3\)

 Index