Index

Differentiation

Stationary points

  1. ?
    ?
    Stationary points are points on the graph where the tangent is horizontal. The derivative at these points is zero:

    \(f'(x)=0\)
    The function has the equation \(f(x)=2x^3-15x^2+36x-25\). Use the derivative to find points on the graph where the tangent is horizontal. Write down the coordinates of these points.
    Solutions:    \(P_1(2,3),~ P_2(3,2)\)
  2. The function has the equation \(f(x)=x^3-3x+1\). Find the stationary points of this function. Write down the coordinates of these points.
    Solutions:    \(P_1(-1,3),~ P_2(1,-1)\)
  3. The function has the equation \(f(x)=x^4-4x^2\).

    (a)   Find the zeros of this function.

    (b)   Using the derivative find the stationary points of this function.

    (c)   Draw the graph.

    Solutions:    (a)  \(x_1=-2,~ x_{2,3}=0,~ x_4=2\);     (b)  \(P_1(-\sqrt{2},-4),~ P_2(0,0),~ P_3(\sqrt{2},-4)\)
  4. The function has the equation \(f(x)=x^3+3x^2+3x+2\).

    (a)   Calculate the derivative of this function.

    (b)   Hence find the stationary points of this function.

    (c)   Draw the graph using your GDC and verify the obtained result.

    Solutions:    (a)  \(f'(x)=3x^2+6x+3\);     (b)  \(P_1(-1,1)\)
  5. The function has the equation \(f(x)={\displaystyle\frac{x}{2}+\frac{2}{x}}\).

    (a)   Calculate the derivative of this function.

    (b)   Hence find the stationary points of this function.

    (c)   Draw the graph using your GDC and verify the obtained result.

    Solutions:    (a)  \(f'(x)=\frac{1}{2}-2x^{-2}\);     (b)  \(P_1(-2,-2),~ P_2(2,2)\)
  6. ?
    ?
    There are three types of stationary points:
    • maxima (maximums)
    • minima (minimums)
    • stationary inflexion points
    The function has the equation:  \(f(x)=x^3-3x^2+1\).

    (a)   Use the derivative to find stationary points.

    (b)   Draw the graph using your GDC.

    (c)   Hence determine the type of each of these points.

    Solutions:    Maximum: \(P_1(0,1)\),  minimum: \(P_2(2,-3)\)
  7. The function has the equation:  \(f(x)=x^4-4x^2\).

    (a)   Use the derivative to find stationary points.

    (b)   Draw the graph using your GDC.

    (c)   Hence determine the type of each of these points.

    Solutions:    Minimum: \(P_1(-\sqrt{2},-4)\),  maximum: \(P_2(0,0)\),  minimum: \(P_3(\sqrt{2},-4)\)
  8. The function has the equation:  \(f(x)=6x^4+8x^3+3\).

    (a)   Use the derivative to find stationary points.

    (b)   Draw the graph using your GDC.

    (c)   Hence determine the nature of each of these points.

    Solutions:    Minimum: \(P_1(-1,1)\),  stationary inflexion point: \(P_2(0,3)\)
  9. Function \(f(x)=\frac{1}{6}x^3-2x^2+ax-4\) has a stationary point at \(x=6\).

    (a)   Find the value of \(a\).

    (b)   Write down all stationary points of this function and draw its graph.

    (c)   Find the zero with the smallest abscissa.

    Solutions:    (a)  \(a=6\);     (b)  \(P_1(6,-4),~ P_2(2,\frac{4}{3})\);     (b)  \(x\approx0.936\)
In following exercises use your GDC to draw the graph. Then use Analyze Graph to find stationary points. Attention: not all inflexion points are stationary.
  1. The function has the equation:  \({\displaystyle f(x)=\frac{2x-1}{x^2}}\).

    (a)   Draw the graph.

    (b)   Find the stationary points and write down their types.

    Solutions:    (b)  maximum: \(P_1(1,1)\)
  2. The function has the equation:  \({\displaystyle f(x)=\frac{x^2-3x}{x^2+3}}\).

    (a)   Draw the graph.

    (b)   Find zeros and asymptotes.

    (c)   Find and classify the stationary points.

    Solutions:    (b)  Zeros: \(x_1=0,~ x_2=3\), no vertical asymptotes, horizontal asymptote: \(y=1\);     (c)  maximum: \(P_1(-3,\frac{3}{2})\), minimum: \(P_2(1,-\frac{1}{2})\)
  3. The function has the equation:  \({\displaystyle f(x)=\frac{6}{x^2-4x+6}}\).

    (a)   Find the zeros and asymptotes, if any.

    (b)   Find and classify the stationary points.

    Solutions:    (a)  No zeros, no vertical asymptotes, horizontal asymptote: \(y=0\);     (b)  maximum: \(P_1(2,3)\)
  4. The function has the equation:  \({\displaystyle f(x)=\frac{1+\ln x}{x}}\).

    (a)   Draw the graph.

    (b)   Find and classify the stationary points.

    Solutions:    (b)  Maximum: \(P_1(1,1)\)
  5. The function has the equation \({\displaystyle y=\frac{x^3-3x^2-15x-19}{9x+9}}\).

    (a)   Draw the graph.

    (b)   Find and classify the stationary points.

    Solutions:    (b)  minimum \(P_1(-2,1)\), stationary inflexion point: \(P_2(1,-2)\)
  6. The function has the equation \(y=\frac{1}{9}x^4+\frac{4}{9}x^3\).

    (a)   Find and classify the stationary points.

    (b)   Find and classify the inflexion points.

    Solutions:    (a)  minimum: \(P_1(-3,-3)\), stationary inflexion point: \(P_2(0,0)\);     (b)  stationary inflexion point: \(P_2(0,0)\), non-stationary inflexion point: \(P_3(-2,-\frac{16}{9})\)

Intervals of increase and decrease

  1. ?
    ?
    Derivative at a given point means the rate of change of this function in the neighbourhood of this point:

    \(f'(x)=\) rate of change
    Consider the function \(f(x)=\frac{1}{4}x^2-x+2\).

    (a)   Find the rate of change at \(x=4\). What happens to \(y\) if you change \(x=4\) to \(x=4.1,~~4.2,~~4.3~\)?

    (b)   Find the rate of change at \(x=6\). What happens to \(y\) if you change \(x=6\) to \(x=6.1,~~6.2,~~6.3~\)?

    Solutions:    (a)  \(f'(4)=1\). Changing \(x\) by 0.1 causes a change in \(y\) by 0.1, too.     (b)  \(f'(6)=2\). Changing \(x\) by 0.1 causes a change in \(y\) by 0.2.
  2. ?
    ?
    The sign of the derivative tells you where the function is increasing or decreasing:

    \(f'(x)\gt 0\) means increase

    \(f'(x)\lt 0\) means decrease
    The function has the equation \(f(x)=x^3-6x^2+9x+2\).

    (a)   Find and classify the stationary points.

    (b)   Find the intervals of increase and decrease.

    Solutions:    (a)  Maximum: \(P_1(1,6)\), minimum: \(P_2(3,2)\);     (b)  the function increases for \(x\lt 1\) and for \(x\gt 3\), it decreases for \(1\lt x\lt 3\)
  3. The function has the equation \({\displaystyle f(x)=\frac{2}{x^2-2x+2}}\).

    (a)   Find and classify the stationary points.

    (b)   Find the intervals of increase and decrease.

    Solutions:    (a)  Maximum: \(P_1(1,2)\);     (b)  the function increases on \((-\infty,1)\), it decreases on \((1,\infty)\)
  4. Function has the equation \(f(x)=\frac{1}{8}x^3-\frac{9}{8}x^2+\frac{15}{8}x-\frac{15}{8}\).

    (a)   Draw the graph of this function.

    (b)   Write down the derivative \(f'(x)\) and draw the graph of the derivative.

    (c)   Find values of \(x\) where the derivative is 0.

    (d)   Find the interval where the derivative is negative.

    Solutions:    (b)  \(f'(x)=\frac{3}{8}x^2-\frac{9}{4}x+\frac{15}{8}\);     (c)  \(x=1\) and \(x=5\) (stationary points);     (d)  for \(1\lt x\lt 5\)
  5. The graph of a function is given (see below).

    (a)   Find values of \(x\), where the function is negative.

    (b)   Find values of \(x\), where the derivative is negative.

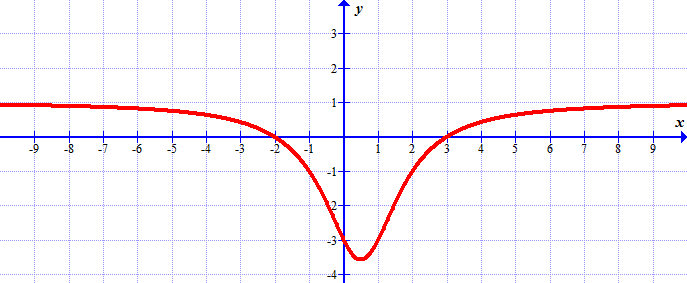
    Function

    Solutions:    (a)  \(f(x)\) is negative for: \(-2\lt x\lt 3\);     (b)  \(f'(x)\) is negative for \(x\lt\frac{1}{2}\)
  6. The following picture shows the graph of the derivative of a function \(f\).

    Graph of the derivative

    (a)   Find values of \(x\), where the function is increasing.

    (b)   Find values of \(x\), where the function is decreasing.

    (c)   Find values of \(x\), where the function has a stationary point.

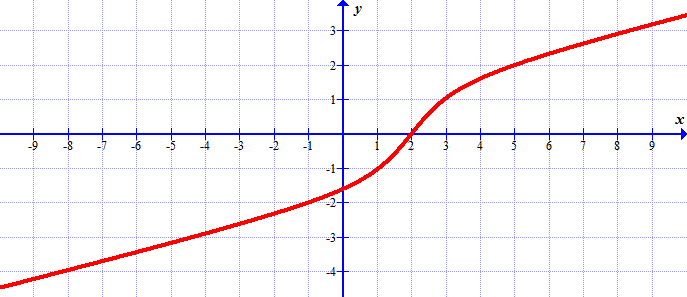
    Solutions:    (a)  \(f(x)\) is increasing for \(x\gt 2\);     (b)  \(f(x)\) is decreasing for \(x\lt 2\);     (c)  \(f(x)\) has a stationary point at \(x=2\) (it's a minimum)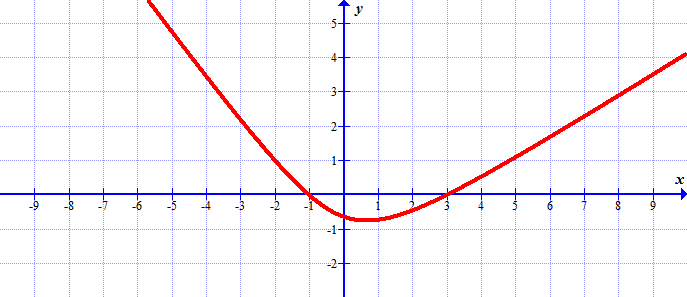
  7. The following picture shows the graph of the derivative of a function \(f\).

    Graph of the derivative

    (a)   Find values of \(x\), where the function is increasing.

    (b)   Find values of \(x\), where the function is decreasing.

    (c)   Find values of \(x\), where the function has a maximum.

    (d)   Find values of \(x\), where the function has a minimum.

    Solutions:    (a)  \(f(x)\) is increasing for \(x\lt -1\) and for \(x\gt 3\);     (b)  \(f(x)\) is decreasing for \(-1\lt x\lt 3\);     (c)  \(f(x)\) has a maximum at \(x=-1\);     (d)  \(f(x)\) has a minimum at \(x=3\)

Applications of the derivative

  1. We would like to build a swimming pool. It should have the form of a cuboid with concrete square bottom and concrete side walls and with the volume \(256~\mathrm{m}^3\). Determine the lengths of the sides so that the building costs will be minimal.
    Solutions:    The area of the bottom and side walls is minimal when \(a=b=8~\mathrm{m},~ h=4~\mathrm{m}\)
  2. A math teacher wants to make wire models of a square and of an oblong (a non-square rectangle) with the sides \(a:b=3:1\). He has a wire \(140~\mathrm{cm}\) long and he's going to split it in two pieces to make both models at the same time. Find the lengths of the sides so that the total area of both figures will be extreme. Is this extreme a maximum or a minimum?
    Solutions:    Square: \(x=15~\mathrm{cm}\), oblong: \(a=30~\mathrm{cm},~ b=10~\mathrm{cm}\), it's a minimum
  3. A craftsman is going to make a cardboard box, open at the top. He has a square piece of cardboard with the dimensions \(60\times60~\mathrm{cm}\). He will cut off a small square with the side \(x\) at each corner and then fold the sides upwards.

    (a)   Find the value of \(x\) that gives the maximum volume of the box.

    (b)   Calculate the sides and the volume of the box in this case.

    Solutions:    (a)  Small square(s): \(x=10~\mathrm{cm}\);     (b)  box: \(a=b=40~\mathrm{cm},~ h=10~\mathrm{cm},~ V=16\,000~\mathrm{cm}^3\)
Powered by MathJax
Index

 Index