Coordinate geometry

Coordinate geometry in two dimensions

1. ?
   ?

   Distance between points $A(x_1,y_1)$ and $B(x_2,y_2)$ can be calculated using the formula:
   
   ${\displaystyle AB=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}}$     or
   
   ${\displaystyle AB=\sqrt{\mathrm{\Delta }{x}^2+\mathrm{\Delta }{y}^2}}$
   Calculate the distance between the given two points:
   

   (a)   $A(2,4),B(14,9)$

   (b)   $P(-3,7),Q(17,-14)$

   (c)   $U(2,-9),V(8,4)$

   Solutions:    (a)  $AB=13$;     (b)  $PQ=29$;     (c)  $UV=\sqrt{205}\approx 14.3$
2. A circle passes through the point $P(5,4)$. Centre of this circle is in the point $C(4,1)$.
   

   (a)   Calculate the radius.

   (b)   Calculate the area of the circle.

   Solutions:    (a)  $r=\sqrt{10}\approx 3.16$;     (b)  $A=10\pi \approx 31.4$
3. Points $A(2,1),B(38,16)$ and $C(18,31)$ are vertices of a triangle $ABC$.
   

   (a)   Calculate the sides of this triangle.

   (b)   Write down the perimeter.

   (c)   Find the area of this triangle.

   Solutions:    (a)  $a=BC=25,b=AC=34,c=AB=39$;     (b)  $P=98$;     (c)  Area $=420$
4. Points $A(-10,-15),B(22,9)$ and $C(17,21)$ are vertices of a triangle $ABC$.
   

   (a)   Calculate the sides of this triangle.

   (b)   Use the cosine rule to calculate the angles.

   (c)   Find the area of this triangle.

   (d)   Find the height $h_c$.

   Solutions:    (a)  $a=BC=13,b=AC=45,c=AB=40$;     (b)  $\alpha \approx {16.3}^{\circ },\beta \approx {104}^{\circ },\gamma \approx {59.5}^{\circ }$;     (c)  Area $=252$;     (d)  $h_c=12.6$
5. ?
   ?

   Midpoint of the straight line segment $AB$ with endpoints $A(x_1,y_1)$ and $B(x_2,y_2)$ has the coordinates:
   
   $M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$
   The endpoints of straight line segments are given. Find the midpoints of these straight line segments.
   

   (a)   $A(1,2),B(7,4)$

   (b)   $C(2,6.5),D(8,1.5)$

   (c)   $E(-2,-1),F(4,13)$

   (d)   $G(-3,5),H(8,-2)$

   Solutions:    (a)  $M(4,3)$;     (b)  $M(5,4)$;     (c)  $M(1,6)$;     (d)  $M(2.5,1.5)$
6. Points $A(-2,10)$ and $B(6,4)$ are diametral points of a circle.
   

   (a)   Find the centre of this circle.

   (b)   Calculate the radius.

   (c)   Find the perimeter and area of this circle.

   Solutions:    (a)  $C(2,7)$;     (b)  $r=5$;     (c)  $P=10\pi \approx 31.4,A=25\pi \approx 78.5$
7. Points $A(-20,6),B(28,20)$ and $C(4,38)$ are vertices of a triangle $ABC$.
   

   (a)   Calculate the sides of this triangle.

   (b)   Show that this is a right-angled triangle.

   (c)   Find the area of this triangle.

   (d)   Find the height $h_c$.

   Median $m_c$ is the line connecting the vertex $C$ and the midpoint of the opposite side $AB$.

   (e)   Calculate the median $m_c$.

   (f)   Find by how many percent is $h_c$ shorter then $m_c$.

   Solutions:    (a)  $a=BC=30,b=AC=40,c=AB=50$;     (b)  Show that $a^2+b^2=c^2$ or calculate $\gamma ={90}^{\circ }$;     (c)  Area $=600$;     (d)  $h_c=24$;     (e)  $m_c=25$;     (f)  $h_c$ is shorter by $4\mathrm{\%}$.
8. Points $A(2,5),B(30,1)$ and $C(8,25)$ are vertices of a triangle $ABC$. Median $m_a$ is the line connecting the vertex $A$ and the midpoint of the opposite side.
   

   (a)   Find the length of the median $m_a$.

   (b)   Calculate the angle $\phi$ formed by $m_a$ and side $c=AB$.

   Solutions:    (a)  $m_a=\sqrt{353}\approx 18.9$;     (b)  $\phi \approx {33.3}^{\circ }$
9. Straight line $L_1$ passes through points $A(1,4)$ and $B(5,2)$.
   

   (a)   Write down the equation of $L_1$.

   (b)   Find the coordinates of the midpoint of $AB$.

   Straight line $L_2$ is perpendicular to $L_1$ and it passes through the midpoint of $AB$. This line is called perpendicular bisector of $AB$.

   (c)   Write down the equation of $L_2$.

   Solutions:    (a)  $y=-\frac{1}{2}x+\frac{9}{2}$;     (b)  $M(3,3)$;     (c)  $L_2:y=2x-3$
10. Endpoints of a straight line segment are given. Write down the equation of the perpendicular bisector of this straight line segment.
    

    (a)   $A(-1,2)$ and $B(9,4)$.

    (b)   $C(1,3)$ and $D(7,5)$.

    (c)   $E(1,8)$ and $F(5,2)$.

    Solutions:    (a)  $y=-5x+23$;     (b)  $y=-3x+16$;     (c)  $y=\frac{2}{3}x+3$
11. Points $A(-5,-4),B(9,-2)$ and $C(1,14)$ are vertices of a triangle $ABC$.
    

    (a)   Write the equation of the perpendicular bisector of the side $AB$.

    (b)   Write the equation of the perpendicular bisector of the side $BC$.

    (c)   Find the intersection point $P$ of these two perpendicular bisectors.

    (d)   Write the equation of the perpendicular bisector of $AC$ and show that it passes through $P$.

    Intersection point of all three perpendicular bisectors is called the circumcentre or the centre of the circumscribed circle. This circle passes through all three vertices of the triangle.

    (e)   Calculate the radius of the circumscribed circle.

    Solutions:    (a)  $y=-7x+11$;     (b)  $y=\frac{1}{2}x+\frac{7}{2}$;     (c)  $P(1,4)$;     (d)  $y=-\frac{1}{3}x+\frac{13}{3}$;     (e)  $r=PA=PB=PC=10$

Applications of 2D geometry

In the following exercises coordinate systems show locations of places on Earth. Distances between places are small and for this reason the curvature of Earth is not taken into consideration. The $x$-axis has the direction from west to east and the $y$-axis has the direction from south to north. Unit in both axes is 1 km.

12. There are three towns at points $A(4,1),B(14,1)$ and $C(9,13)$. Towns are connected with three roads: $AB,BC$ and $AC$.
    

    (a)   Calculate the distances $AB,BC$ and $AC$.

    The region enclosed between the roads is a natural reserve.

    (b)   Calculate the area of this reserve.

    Solutions:    (a)  $AB=10\mathrm{km},AC=BC=13\mathrm{km}$;     (b)  Area: $60{\mathrm{km}}^2$
13. There are three towns: town $A(1,1)$, town $B(6,4)$ and town $C(10,8)$. Towns $A$ and $B$ are connected by a road. Towns $B$ and $C$ are connected by a road, too.
    

    (a)   Draw these three towns and two roads in a coordinate system.

    (b)   Calculate the distances $AB$ and $BC$.

    There's no direct road from $A$ to $C$, but citizens are considering the possibility of building such a direct road.

    (c)   Calculate the direct distance from $A$ to $C$.

    (d)   Now a citizen of town $A$, who wants to reach $C$, must travel from $A$ to $B$ and then from $B$ to $C$. Calculate the distance he must travel this way.

    (e)   Compare the distances calculated in (c) and (d). How much shorter would the direct road be? Does it make sense to build a direct road?

    Solutions:    (b)  $AB=5.83,BC=5.66$;     (c)  $AC=11.40$;     (d)  $AB+BC=11.48$;     (e)  It doesn't make sense. The direct road would be only 86 metres shorter.
14. There are three towns: $A(-2,-3),B(1,7)$ and $C(5,1)$. Towns $A$ and $B$ are connected by a road. Towns $B$ and $C$ are connected by a road, too.
    

    (a)   Draw these three towns and two roads in a coordinate system.

    (b)   Calculate the distances $AB$ and $BC$. Calculate the sum of these distances.

    The government is planning to build a direct road from $A$ to $C$.

    (c)   Calculate the length of the planned road $AC$.

    (d)   Calculate how much shorter will be the voyage from $A$ to $C$ when the new road is built. Does it make sense to build a direct road?

    Solutions:    (b)  $AB=10.4,BC=7.21,AB+BC=17.65$;     (c)  $AC=AC=8.06$;     (d)  $AB+BC-AC=9.59\mathrm{km}=$ much shorter, so it makes sense to build a direct road.
15. A postman starts his working day at the post office which is located at the origin of the coordinate system $O(0,0)$. Then he must deliver the mail to three places located at points $A(2,5),B(6,2)$ and $C(2,3)$. He usually starts at $O$, goes to $A$, than continues his way to $B$, continues to $C$ and returns to $O$. ($O⟶A⟶B⟶C⟶O$)
    

    (a)   Draw a diagram.

    (b)   Calculate the total length of his way. First calculate the distances $OA,AB,BC$ and $CO$. Then add them together.

    (c)   Now this postman is considering another route: $O⟶A⟶C⟶B⟶O$. Calculate the total length of this new route. Is this route shorter?

    (d)   Is there an even shorter way? Consider $O⟶C⟶A⟶B⟶O$.

    Solutions:    (b)  $OA+AB+BC+CO=18.1$;     (c)  $OA+AC+CB+BO=17.8$; (It's shorter.)     (d)  $OC+CA+AB+BO=16.9$ (Even shorter.)
16. Consider three towns at points $A(-6,6),B(13,-3)$ and $C(16,12)$. Town $A$ has an electrical power plant. Power lines are planned to transmit electric power to towns $B$ and $C$.
    

    (a)   Calculate the distances $AB,AC$ and $BC$.

    (b)   Calculate the total length of the power lines connecting $A$ to $B$ and $A$ to $C$.

    (c)   Calculate the total length of the power line connecting $A$ to $B$ and then $B$ to $C$.

    A mathematician proposed that a junction should be built at point $J(10,4)$ and then connected to all three towns. He claims that his solution is even better.

    (d)   Calculate the total length of the power lines connecting $J$ to $A$, to $B$ and to $C$.

    Solutions:    (a)  $AB\approx 21.0,AC\approx 22.8,BC\approx 15.3$;     (b)  $AB+AC\approx 43.8$;     (c)  $AB+BC\approx 36.3$;     (d)  $JA+JB+JC\approx 33.7$
17. Consider three towns at points $A(0,0),B(24,-10)$ and $C(24,10)$. Town $A$ has an electrical power plant. Power lines are planned to transmit electric power to a junction $J(x,0)$ and from there to towns $B$ and $C$.
    

    (a)   Calculate the distances $AJ,BJ$ and $CJ$ depending on the unknown coordinate $x$.

    (b)   Write down the function describing the total length of the power lines connecting $AJ,BJ$ and $CJ$ together.

    (c)   Use your GDC to draw this function and find $x$ which determines the optimal location of the junction.

    (d)   Find the total length of power lines in case of the optimal location of the junction.

    Solutions:    (a)  $AJ=x,BJ=CJ=\sqrt{(24-x{)}^2+{10}^2}$;     (b)  $f(x)=x+2\cdot \sqrt{(24-x{)}^2+{10}^2}$;     (c)  function has a minimum at $x\approx 18.2$, so junction must be located at $J(18.2,0)$;     (d)  the total length in this case is $\approx 41.3$
18. Bearing is the angle between north and direction of a vehicle, ship or airplane. It's measured clockwise and often written using three figures.
    Find the bearings of the flights on the next picture. Each flight is represented by an arrow drawn from the departure point to the landing point.
    
    Solutions:    (a)  ${90}^{\circ }$ (often written as: ${090}^{\circ }$ or also: 0-9-0);     (b)  $0^{\circ }$ (or ${000}^{\circ }$);     (c)  ${180}^{\circ }$;     (d)  ${45}^{\circ }$ (or ${045}^{\circ }$);     (e)  ${135}^{\circ }$;     (f)  ${26.6}^{\circ }$ (or ${026.6}^{\circ }$)
19. ?
    ?

    Traveling the distance $d$ on a bearing $\beta$ is connected with formulas:
    
    $\mathrm{\Delta }x=d\sin \beta$
    
    $\mathrm{\Delta }y=d\cos \beta$
    
    $\tan \beta =\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}$
    An airplane flies from the town $A(0,0)$ to the town $B(175,280)$.
    

    (a)   Find the distance between these two towns.

    (b)   Write down the bearing (assuming that the plane flies in a straight line).

    Solutions:    (a)  Distance $\approx 330\mathrm{km}$;     (b)  bearing $\approx {32.0}^{\circ }$
20. An airplane flies from the town $A(10,-30)$ to the town $B(94,90)$ and then it returns to $A$.
    

    (a)   Find the total length of the flight.

    (b)   Write down the bearing on the way from $A$ to $B$.

    (c)   Write down the bearing on the way from $B$ back to $A$.

    Solutions:    (a)  Total distance $\approx 293\mathrm{km}$;     (b)  bearing $\approx {35}^{\circ }$;     (c)  bearing $\approx {215}^{\circ }$
21. An airplane flies from the town $A(0,0)$ to the town $B(480,360)$ where it makes a stop for 1 hour. After that it continues the flight from $B$ to $C(330,440)$. At $C$ it makes a stop for 1 hour again and then it returns to $A$.
    

    (a)   Write down the bearings for each part of this flight.

    (b)   Find the total length of the flight.

    The flight started at 9.00 AM. When in the air, this airplane flies at 600 km/h.

    (c)   Find out the time of return to town $A$. Write the time in hours and minutes.

    Solutions:    (a)  Bearings: $\beta (AB)={53.1}^{\circ }$, $\beta (BC)={298}^{\circ }$, $\beta (CA)={217}^{\circ }$ ;     (b)  $AB+BC+CA=600+170+550=1320\mathrm{km}$;     (c)  return at 13.12 (or 1.12 PM).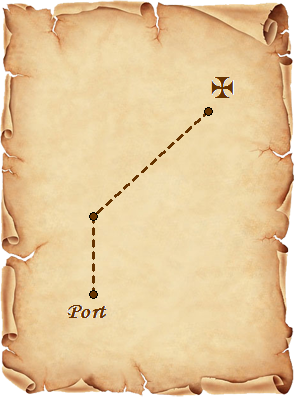
22. Three ships leave the port $A(0,0)$.
    – The first ship travels 58 km on a bearing 15° and arrives to the port $B$.
    – The second ship travels 41 km on a bearing 137° and arrives to the port $C$.
    – The third ship travels 83 km on a bearing 189° and arrives to the port $D$.
    Find the coordinates of ports $B,C$ and $D$.
    Solutions:    $B(15,56),C(28,-30),D(-13,-82)$
23. A airplane departs from the airport $A(0,0)$. It travels 89 km on a bearing 26°. In this point $B$ it makes a 90° turn to the right and travels for another 89 km and arrives to the town $C$. Find the coordinates of $B$ and $C$.
    Solutions:    $B(39,80),C(119,41)$
24. Alex found a map showing the way to the island with a hidden treasure. It says: Leave port and sail to the north for 30 km. Continue to sail 58 km to north-east. Here it is. Alex decided to follow the instructions.
    

    (a)   Write down the coordinates of the treasure island.

    Zelda secretly took a picture of this map. She decided to go searching the treasure island, too. She wants to be the first to get to the island, so she is going to take a shortcut: she will follow the straight line from the port to the island.

    (b)   Find the bearing Zelda will have to follow. Find the length of her travel, too.

    Solutions:    (a)  $A(41,71)$;     (b)  bearing 30°, distance 82 km

Voronoi diagrams

25. Consider points $A(-3,3)$ and $B(5,-1)$.
    

    (a)   Draw points $A$ and $B$ in a coordinate system.

    (b)   Show that point $P(2,3)$ is equally distant from $A$ and $B$.

    There are many other points equally distant from $A$ and $B$. All these points form a straight line.

    (c)   Draw this straight line and write down its equation. How is this line called?

    (d)   Find points which are closer to $A$. Colour them in red.

    (e)   Find points which are closer to $B$. Colour them in blue.

    Solutions:    (b)  $AP=5,BP=5$;     (c)  $y=2x-1$    It's the perpendicular bisector of the line segment $[AB]$.
    
    
26. Points $A(-2,1),B(3,-4)$ and $C(6,5)$ are given.
    

    (a)   Draw these points in a coordinate system.

    (b)   Write the equation of the line of points equally distant from $A$ and $B$.

    (c)   Write the equation of the line of points equally distant from $A$ and $C$.

    (d)   Write the equation of the line of points equally distant from $B$ and $C$.

    All three lines pass through a common point. This point is called the Voronoi vertex.

    (e)   Find the coordinates of the Voronoi vertex $V$.

    (f)   Find points which are closer to $A$ than to $B$ or $C$. Colour them in red.

    (g)   Find points which are closer to $B$ than to $A$ or $C$. Colour them in green.

    (h)   Find points which are closer to $C$ than to $A$ or $B$. Colour them in blue.

    (i)   Draw the boundaries of these three regions in black. They are called Voronoi edges. Which lines do they follow?

    Solutions:    (b)  $y=x-2$;     (c)  $y=-2x+7$;     (d)  $y=-\frac{1}{3}x+2$;     (e)  $V(3,1)$;     (i)  Boundary between red and green follows $y=x-2(\mathrm{for}x<3)$,   boundary between red and blue follows $y=-2x+7(\mathrm{for}x<3)$,   boundary between blue and green follows $y=-\frac{1}{3}x+2(\mathrm{for}x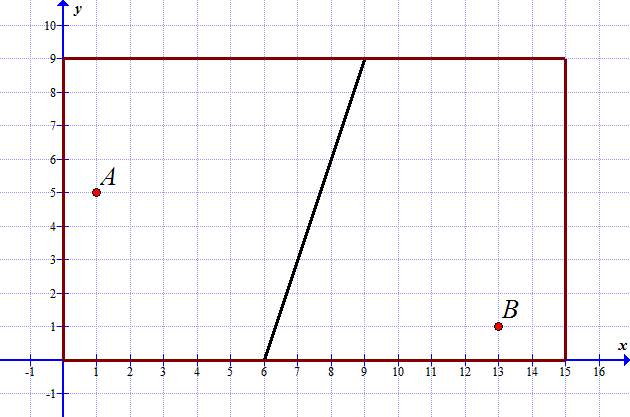>3)$
    
    
27. A town has the form of a rectangle $15\times 9\mathrm{km}$. There are two shopping centres in this town, at $A(1,5)$ and at $B(13,1)$, as shown in the following picture:
    
    People always go shopping to the nearest shopping centre, so the town is split in two regions.
    

    (a)   Find the equation of the border line of these two regions.

    (b)   Calculate the areas of these two regions.

    A new shopping centre has opened at $C(7,7)$. People still go shopping to the nearest shopping centre, so the town is split in three regions now.

    (c)   Draw the appropriate Voronoi diagram.

    (d)   Find equations of new border lines.

    (e)   Find areas of all three regions.

    Solutions:    (a)  $y=3x-18(\mathrm{for}6<x<9)$;     (b)  $A=67.5$ (for each of them);     (d)  $y=-3x+18(\mathrm{for}3<x<6)$ and $y=x-6(\mathrm{for}6<x<15)$;     (e)  $A_1=40.5$, $A_2=54$, $A_3=40.5$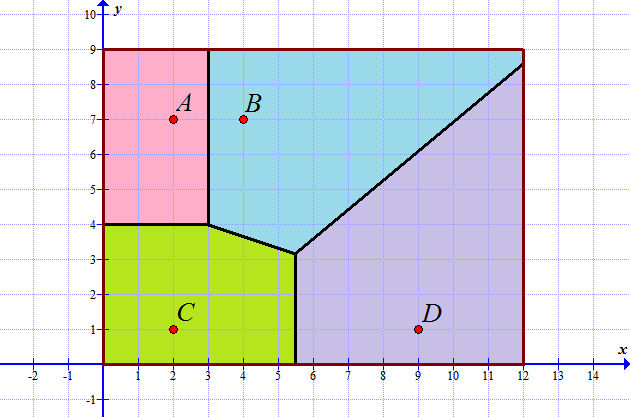
    
    
28. A town has the form of a rectangle $12\times 9\mathrm{km}$. There are four schools in this town, located at $A(2,7)$, $B(4,7)$, $C(2,1)$ and $D(9,1)$. The following picture shows the school districts. They are organized so that every child attends the school nearest to his home.
    
    

    (a)   Find the coordinates of the point which is equally distant to schools $A,B$ and $C$.

    (b)   Write down the equation of the line which determines the border between $B$ and $C$.

    (c)   Calculate the coordinates of the vertex where school districts $B,C$ and $D$ meet.

    Solutions:    (a)  $V_1(3,4)$;     (b)  $y=-\frac{1}{3}x+5(\mathrm{for}3<x<5.5)$;     (c)  $V_2(5\frac{1}{2},3\frac{1}{6})\approx (5.5,3.17)$

Coordinate geometry in three dimensions

29. ?
    ?

    Distance between points $A(x_1,y_1,z_1)$ and $B(x_2,y_2,z_2)$ can be calculated using the formula:
    
    ${\displaystyle AB=\sqrt{\mathrm{\Delta }{x}^2+\mathrm{\Delta }{y}^2+\mathrm{\Delta }{z}^2}}$
    Calculate the distance between the given two points:
    

    (a)   $A(1,2,0),B(5,10,19)$

    (b)   $C(-3,-2,4),D(13,10,-11)$

    (c)   $E(0,20,-13),F(15,-3,4)$

    Solutions:    (a)  $AB=21$;     (b)  $CD=25$;     (c)  $EF=\sqrt{1043}\approx 32.3$
30. Consider the triangle with vertices: $A(-1,7,5),B(5,1,5)$ and $C(3,5,1)$.
    

    (a)   Find the lengths of all three sides.

    (b)   Calculate the angles.

    Solutions:    (a)  $AB=6\sqrt{2},AC=BC=6$;     (b)  $\hat{A}=\hat{B}={45}^{\circ },\hat{C}={90}^{\circ }$
31. A triangle has the vertices: $A(1,1,1),B(10,7,3)$ and $C(6,19,0)$.
    

    (a)   Find the lengths of all three sides.

    (b)   Calculate the largest angle in this triangle.

    Solutions:    (a)  $a=BC=13,b=AC=\sqrt{350}\approx 18.7,c=AB=11$;     (b)  $\beta =A\hat{B}C\approx {102}^{\circ }$   (Hint: The largest angle is opposite to the largest side.)
32. A triangle has the vertices: $P(-3,0,2),Q(4,4,5)$ and $R(6,8,9)$.
    

    (a)   Find the lengths of all three sides.

    (b)   Calculate the area.

    Solutions:    (a)  $PQ=\sqrt{74}\approx 8.60,QR=6,PR=\sqrt{194}\approx 13.9$;     (b)  $A=15$
33. ?
    ?

    Midpoint of the straight line segment $AB$ with vertices $A(x_1,y_1,z_1)$ and $B(x_2,y_2,z_2)$ has the coordinates:
    
    $M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},\frac{z_1+z_2}{2})$
    The endpoints of straight line segments are given. Calculate the midpoints of these segments.
    

    (a)   $A(4,3,9)$ and $B(8,5,7)$

    (b)   $C(-2,5,4)$ and $D(6,-3,-10)$

    (c)   $E(1,0,7)$ and $F(-1,3,-2)$

    Solutions:    (a)  $M(6,4,8)$;     (b)  $M(2,1,-3)$;     (c)  $M(0,1.5,2.5)$
34. Point $M(2,9,k)$ is the midpoint of the line segment $AB$ with vertices $A(7,13,20)$ and $B(-3,n,8)$. Find $k$ and $n$.
    Solutions:    $k=14,n=5$
35. Point $M(5,11,8)$ is the midpoint of the line segment $AB$. Find coordinates of $A$ if $B(10,7,9)$ is given.
    Solutions:    $A(0,15,7)$
36. Points $A(1,12,7)$ and $E(21,20,19)$ are given. Points $B,C$ and $D$ split the straight line segment $AE$ in four equal parts. Find the coordinates of $B,C$ and $D$ using the following procedure:
    

    (a)   First, find coordinates of $C$ which is the midpoint of $AE$.

    (b)   Then, find coordinates of $B$ which is the midpoint of $AC$.

    (c)   Then, find coordinates of $D$ which is the midpoint of $CE$

    Solutions:    (a)  $C(11,16,13)$;     (b)  $B(6,14,10)$;     (c)  $D(16,18,16)$
37. A triangle has the vertices: $A(-9,2,7),B(1,8,1)$ and $C(9,6,17)$. Median $m_a$ connects vertex $A$ with the midpoint of the opposite side.
    

    (a)   Find the midpoint of the side $BC$.

    (b)   Find the length of the median $m_a$.

    (c)   Calculate the acute angle between $m_a$ and side $BC$.

    Solutions:    (a)  $M(5,7,9)$;     (b)  $m_a=15$;     (c)  $\phi \approx {60.2}^{\circ }$

 Index